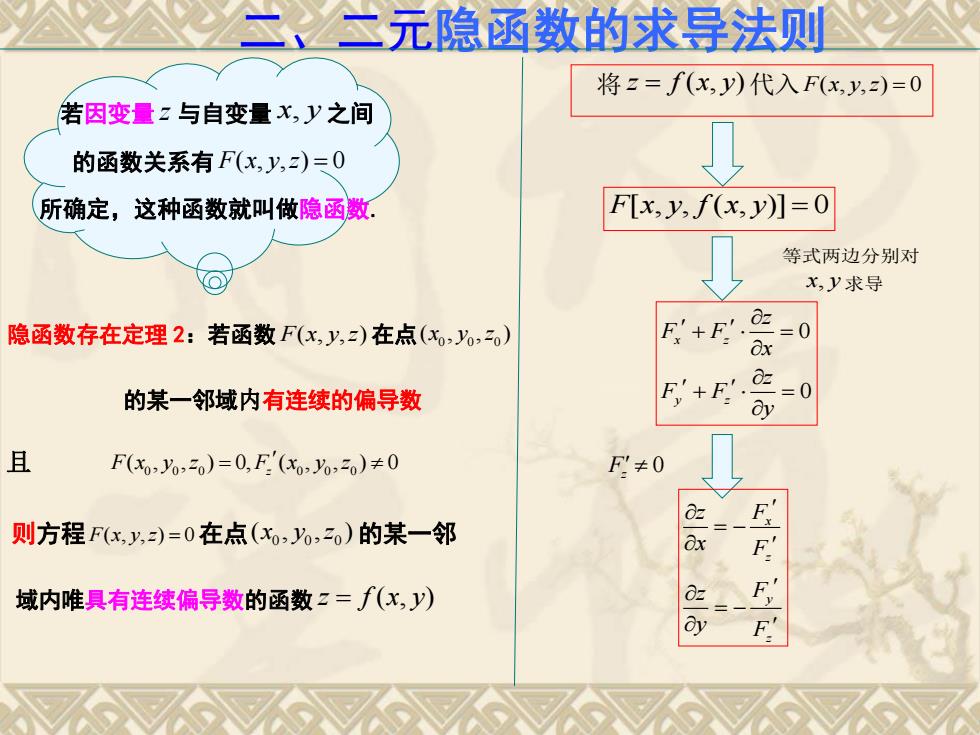
二元隐函数的求导法则 将z=f(x,y)代入F(x,y,z)=0 若因变量z与自变量x,y之间 的函数关系有F(x,y,)三0 所确定，这种函数就叫做隐函数. F[x,y,f(x,y)]=0 等式两边分别对 x,y求导 隐函数存在定理2：若函数F(x,y,)在点(x,,) F'+F'. =0 Ox 的某一邻域内有连续的偏导数 F+E 2二0 ay 且 F(x0,,0)=0,F'(xo,0,0)≠0 F≠0 则方程Fx,y,)=0在点(x,%,0)的某一邻 域内唯具有连续偏导数的函数z=∫(x,y) F, 二、二元隐函数的求导法则 若因变量 z 与自变量 x y, 之间 的函数关系有 F x y z ( , , ) 0  所确定，这种函数就叫做隐函数. 隐函数存在定理 2：若函数 F x y z ( , , ) 在点 0 0 0 ( , , ) x y z 的某一邻域内有连续的偏导数 且 0 0 0 0 0 0 ( , , ) 0, ( , , ) 0 F x y z F x y z z    则方程F x y z ( , , ) 0  在点 0 0 0 ( , , ) x y z 的某一邻 域内唯具有连续偏导数的函数 z f x y  ( , ) 将 z f x y  ( , ) 代入F x y z ( , , ) 0  F x y f x y [ , , ( , )] 0  等式两边分别对 x y, 求导 0 0 x z y z z F F x z F F y               0 F z   x z y z z F x F z F y F            