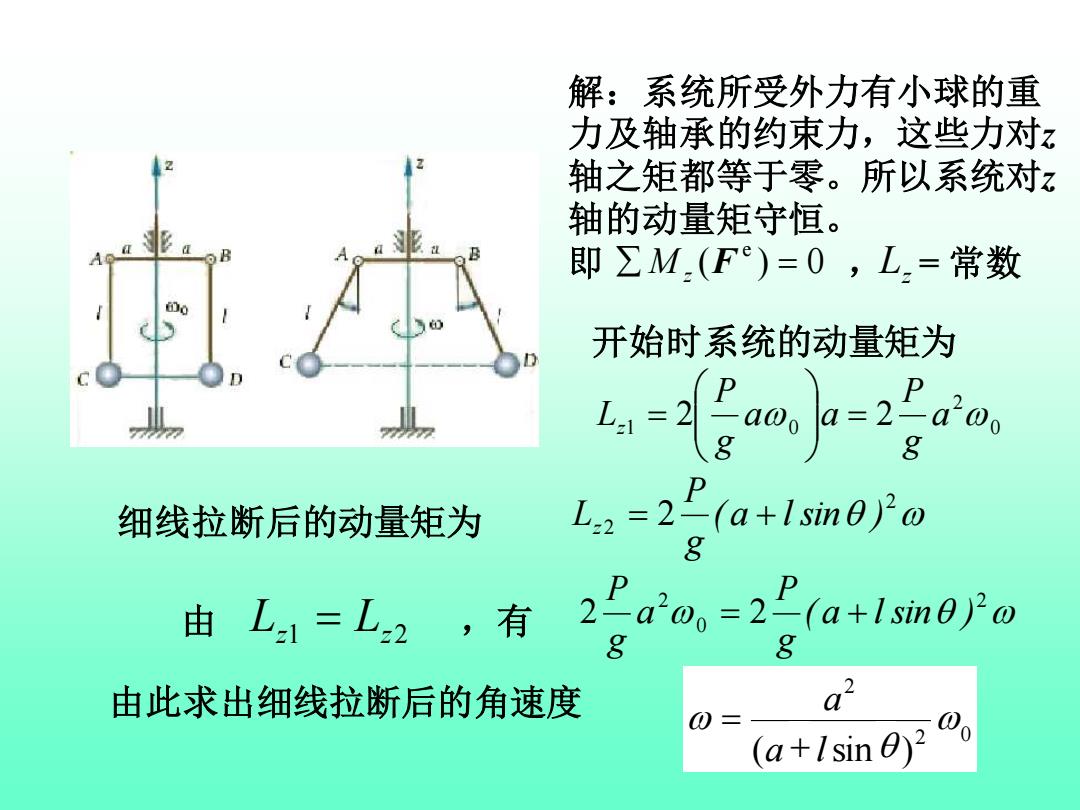
解：系统所受外力有小球的重 力及轴承的约束力，这些力对z 轴之矩都等于零。所以系统对z 轴的动量矩守恒。 即∑M,(F)=0,L,=常数 开始时系统的动量矩为 Laagun 2o g 细线拉断后的动量矩为 L2=2(a+1sim0)'0 由L1=L2，有 2营ra-a+liam8re 由此求出细线拉断后的角速度 23 (a+lsin解：系统所受外力有小球的重 力及轴承的约束力，这些力对z 轴之矩都等于零。所以系统对z 轴的动量矩守恒。 即 ( ) 0 ， = 常数 e  M z F = Lz 开始时系统的动量矩为 0 2 1 0 2  2 a  g P a a g P Lz =         = 细线拉断后的动量矩为   2 2 2 ( a l sin ) g P Lz = + 由 Lz1 = Lz2 ，有    2 0 2 2 2 ( a l sin ) g P a g P = + 由此求出细线拉断后的角速度 2 0 2 ( sin )    a l a + =