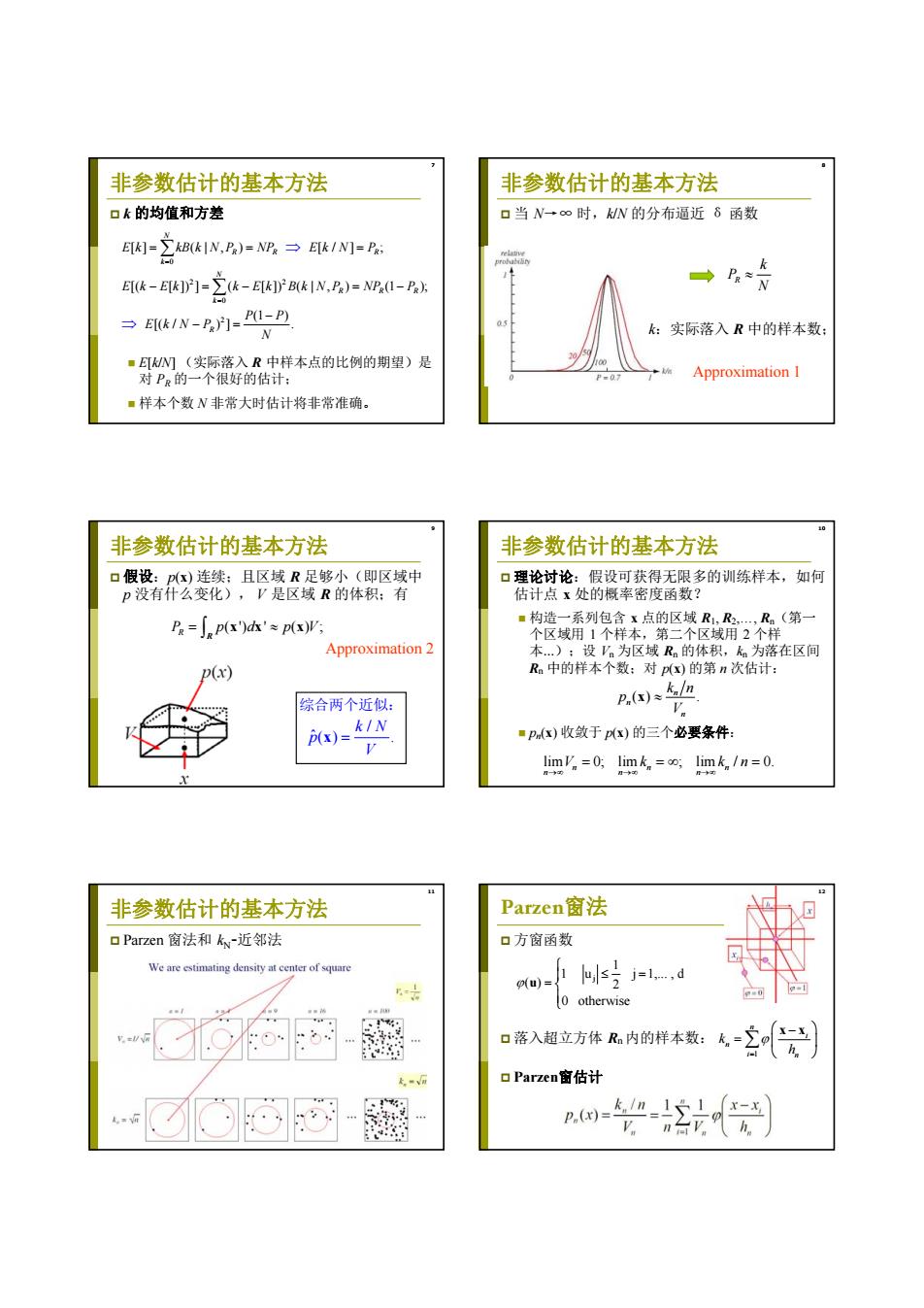
非参数估计的基本方法 非参数估计的基本方法 口k的均值和方差 口当N一∞时，MN的分布逼近6函数 E=之BkIN,P)=NR,→/N]=P Ek-E[kJ]=∑k-E[B(kN,PR)=NP(I-P方 →4 k-0 →Ek1N-P月=P1-P N k:实际落入R中的样本数： ■E[N(实际落入R中样本点的比例的期望)是 对PR的一个很好的估计： P-07 Approximation I ■样本个数N非常大时估计将非常准确。 0 非参数估计的基本方法 非参数估计的基本方法 口假设：px)连续；且区域R足够小（即区域中 口理论讨论：假设可获得无限多的训练样本，如何 p没有什么变化)，V是区域R的体积：有 估计点x处的概率密度函数？ Pa=px')k'≈px) ■构造一系列包含x点的区域R1,R2,R。(第一 个区域用1个样本，第二个区域用2个样 Approximation 2 本)：设V。为区域R的体积，k为落在区间 Ra中的样本个数：对px)的第n次估计： 综合两个近似： P.(x)kln 0)s/N ■Px)收敛于px)的三个必要条件： V limV =0;limk oo;lim k /n=0. 非参数估计的基本方法 Parzen窗法 口Parzen窗法和kw-近邻法 口方窗函数 We are estimating density at center of square 1 o(u)= j=l…,d 0 otherwise 口落入超立方体Rn内的样本数： Parzen窗估计 ☑心心- P.(x)=7 非参数估计的基本方法  k 的均值和方差  E[k/N] （实际落入 R 中样本点的比例的期望）是 对 PR 的一个很好的估计；  样本个数 N 非常大时估计将非常准确。 0 2 2 0 2 [] ( | , ) [ / ] ; [( [ ]) ] ( [ ]) ( | , ) (1 ); (1 ) [( / ) ] . N RR R k N R RR k R E k kB k N P NP E k N P E k E k k E k B k N P NP P P P EkN P N                8 非参数估计的基本方法  当 N→∞ 时，k/N 的分布逼近 δ 函数 Approximation 1 R k P N  k：实际落入 R 中的样本数；  假设：p(x) 连续；且区域 R 足够小（即区域中 p 没有什么变化）， V 是区域 R 的体积；有 9 非参数估计的基本方法 ( ') ' ( ) ; P p d pV R    xx x R Approximation 2 / ˆ() . k N p V x  综合两个近似： 10 非参数估计的基本方法  理论讨论：假设可获得无限多的训练样本，如何 估计点 x 处的概率密度函数？  构造一系列包含 x 点的区域 R1, R2,…, Rn（第一 个区域用 1 个样本，第二个区域用 2 个样 本…）；设 Vn 为区域 Rn 的体积，kn 为落在区间 Rn 中的样本个数；对 p(x) 的第 n 次估计：  pn(x) 收敛于 p(x) 的三个必要条件： () . n n n k n p V x  lim 0; lim ; lim / 0. nn n nn n V k kn       11 非参数估计的基本方法  Parzen 窗法和 kN-近邻法 12 Parzen窗法  方窗函数  落入超立方体 Rn 内的样本数：  Parzen窗估计 j 1 1 u j 1,... , d ( ) 2 0 otherwise          u 1 n i n i n k h            x x