
第三章 概率密度函数的估计 非参数估计 2010-10-18 直方图法 直方图法 口基本思路:户(x)是px)的离散近似 口平滑参数:小窗个数/尺寸(bin size)) ■将观测向量x的每个分量分成k个等间隔小窗 M=3 1M=20 p(x) P(x) 2(x) (bin):x∈E,即形成d个小舱: P(x) ■统计落入各个小舱内的样本数 H0=210,eBi=12,m Oversmoothing M=10 =50 ·正规化 p(x) P】 0肥 P(x 非参数估计的基本方法 非参数估计的基本方法 口基本思路:用某核函数表示某一样本对待估计的 口基本事实:一个向量x落在区域R中的概率为 密度函数的贡献,所有样本所作贡献的线性组合 (函数之和)视作对某点概率密度p(x)的估计。 P=∫npx'h ,(s)=2x-x》 。根据P()抽取N个独立同分布的样本,则有 Pk)=CPI-P)-=BkIN,P方 口P):N个样本中有k个落入区域R的概率: 口Pe:样本x落入区域R的概率: 口B(k|N,P):k的二项分布。 玉】单参数估计的蒂本 图多《每个样本的质献随距离变化的非参数结计
第三章 概率密度函数的估计 2010-10-18 非参数估计 3 直方图法 基本思路: 是 的离散近似 将观测向量 x 的每个分量分成 k 个等间隔小窗 (bin);x∈Ed,即形成 kd 个小舱; 统计落入各个小舱内的样本数 正规化 ( ) ˆ P x p( ) x 1 ( ) ( ), 1,2, , ; n j i j Hi I B i m x ( ) ˆ() . H i p i NV 平滑参数:小窗个数/尺寸 (bin size) 4 直方图法 5 非参数估计的基本方法 基本思路:用某核函数表示某一样本对待估计的 密度函数的贡献,所有样本所作贡献的线性组合 (函数之和)视作对某点概率密度 p(x) 的估计。 1 ˆ ( ) ( ). n N i i p x xx 6 非参数估计的基本方法 基本事实:一个向量 x 落在区域 R 中的概率为 根据 p(x) 抽取 N 个独立同分布的样本,则有 P(k):N个样本中有 k 个落入区域 R 的概率; PR:样本 x 落入区域 R 的概率; B(k | N, P):k 的二项分布。 ( ') '; P pd R x x R ( ) (1 ) ( | , ); k k Nk Pk C P P Bk NP NR R R
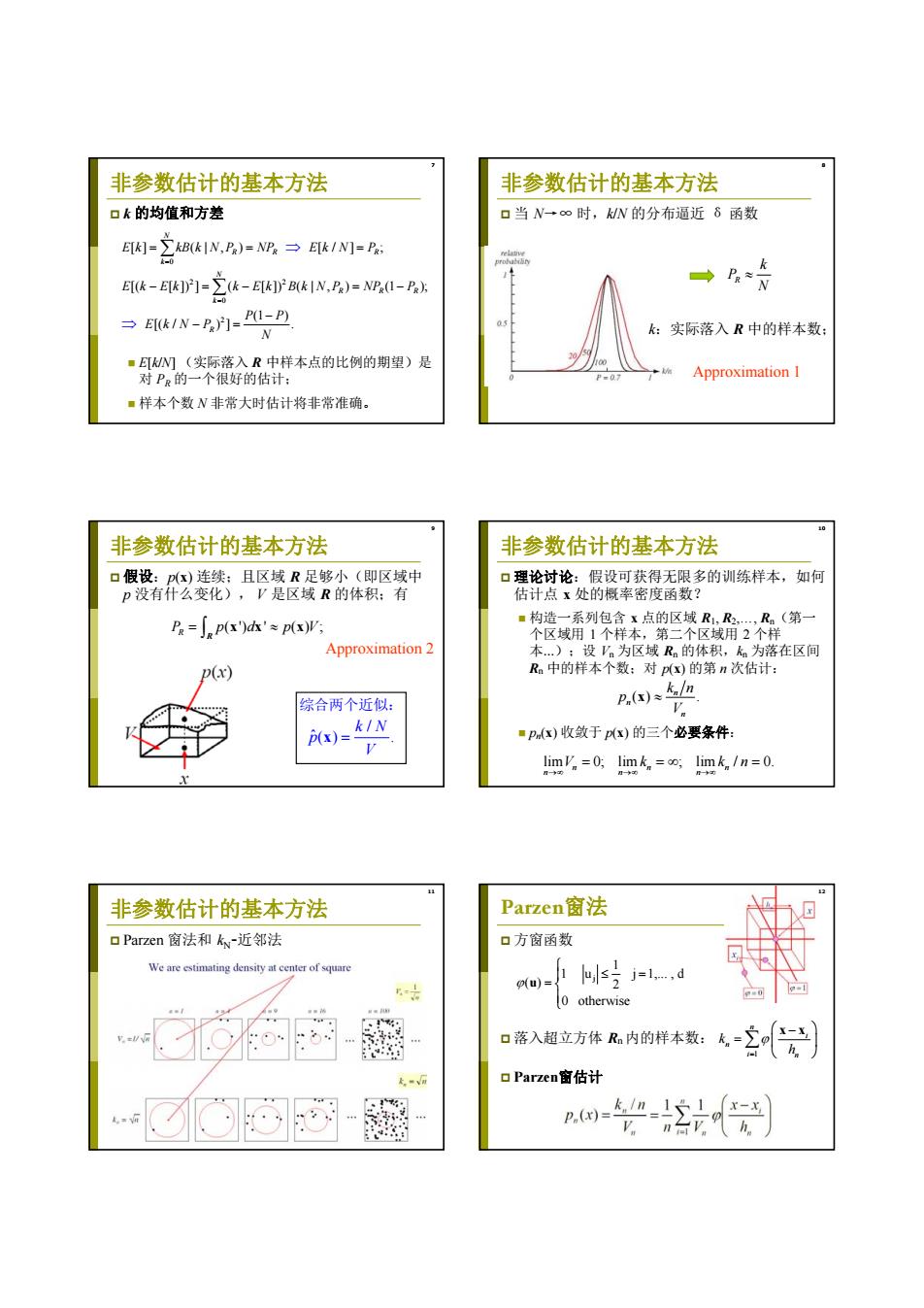
非参数估计的基本方法 非参数估计的基本方法 口k的均值和方差 口当N一∞时,MN的分布逼近6函数 E=之BkIN,P)=NR,→/N]=P Ek-E[kJ]=∑k-E[B(kN,PR)=NP(I-P方 →4 k-0 →Ek1N-P月=P1-P N k:实际落入R中的样本数: ■E[N(实际落入R中样本点的比例的期望)是 对PR的一个很好的估计: P-07 Approximation I ■样本个数N非常大时估计将非常准确。 0 非参数估计的基本方法 非参数估计的基本方法 口假设:px)连续;且区域R足够小(即区域中 口理论讨论:假设可获得无限多的训练样本,如何 p没有什么变化),V是区域R的体积:有 估计点x处的概率密度函数? Pa=px')k'≈px) ■构造一系列包含x点的区域R1,R2,R。(第一 个区域用1个样本,第二个区域用2个样 Approximation 2 本):设V。为区域R的体积,k为落在区间 Ra中的样本个数:对px)的第n次估计: 综合两个近似: P.(x)kln 0)s/N ■Px)收敛于px)的三个必要条件: V limV =0;limk oo;lim k /n=0. 非参数估计的基本方法 Parzen窗法 口Parzen窗法和kw-近邻法 口方窗函数 We are estimating density at center of square 1 o(u)= j=l…,d 0 otherwise 口落入超立方体Rn内的样本数: Parzen窗估计 ☑心心- P.(x)=
7 非参数估计的基本方法 k 的均值和方差 E[k/N] (实际落入 R 中样本点的比例的期望)是 对 PR 的一个很好的估计; 样本个数 N 非常大时估计将非常准确。 0 2 2 0 2 [] ( | , ) [ / ] ; [( [ ]) ] ( [ ]) ( | , ) (1 ); (1 ) [( / ) ] . N RR R k N R RR k R E k kB k N P NP E k N P E k E k k E k B k N P NP P P P EkN P N 8 非参数估计的基本方法 当 N→∞ 时,k/N 的分布逼近 δ 函数 Approximation 1 R k P N k:实际落入 R 中的样本数; 假设:p(x) 连续;且区域 R 足够小(即区域中 p 没有什么变化), V 是区域 R 的体积;有 9 非参数估计的基本方法 ( ') ' ( ) ; P p d pV R xx x R Approximation 2 / ˆ() . k N p V x 综合两个近似: 10 非参数估计的基本方法 理论讨论:假设可获得无限多的训练样本,如何 估计点 x 处的概率密度函数? 构造一系列包含 x 点的区域 R1, R2,…, Rn(第一 个区域用 1 个样本,第二个区域用 2 个样 本…);设 Vn 为区域 Rn 的体积,kn 为落在区间 Rn 中的样本个数;对 p(x) 的第 n 次估计: pn(x) 收敛于 p(x) 的三个必要条件: () . n n n k n p V x lim 0; lim ; lim / 0. nn n nn n V k kn 11 非参数估计的基本方法 Parzen 窗法和 kN-近邻法 12 Parzen窗法 方窗函数 落入超立方体 Rn 内的样本数: Parzen窗估计 j 1 1 u j 1,... , d ( ) 2 0 otherwise u 1 n i n i n k h x x

14 Parzen窗法 Parzen窗法 口Parzen?窗估计p.(x)为合理的密度函数的条件: 口常用窗函数 窗函数本身是合法的密度函数 ·方窗 p(u)20: [o(u)du=1; ■正态窗: p= ■指数窗: (u)=exp(-lul) 可2片h ■三角窗:)= 1-4if叫s1 0 otherwise 22h-2到h1 ■超球窗: ∫1ifs1 p(u)= 0 otherwise Parzen窗法 Parzen窗法 口Parzen估计量pax)是渐进无偏和平方误差一致 口窗宽hn的影响 估计的限制条件: ·p(x)在x点连续: (1) p(u)20 p.=2d.-x方 n (2) ∫p(u)d=上 ■hn很大→6。的强度低:且距离点x远近不同 ■窗函数满足下列条件: (3) sup(u)< 的样本的6。相差不大P(x)是n个宽度较 大且变化缓慢的函数的叠加,是平滑、低分辨力 (4) o4=4 的估计。 ·窗宽约束: (5) ■hn很小→6(x-x)的峰值大→pa(x)是n个 lim=0; 以样本点为中心的尖脉冲的叠加,统计变动大, (6) lmn水.=o 是充满噪声的估计。 Parzen窗法 Parzen窗法 口窗宽hm是平滑参数,需优化,根据样本的数量 口例1:px)和p(u)均是正态分布 选择。 h.=01 p(x)-N(0,I方 A √2π h.=h/n: 个 个N
13 Parzen窗法 Parzen窗估计 pn(x) 为合理的密度函数的条件: 窗函数本身是合法的密度函数 1 1 1 1 1 ( ) 11 1 ( ) 1. n i n i n n n n i i i n n pd d nV h d d nV h n x x xx x x x x uu ( ) 0; ( ) 1; d u uu 14 Parzen窗法 常用窗函数 方窗 正态窗: 指数窗: 三角窗: 超球窗: 1 1 2 ( ) exp ~ (0,1) 2 2 u uN ( ) exp | | u u 1 if 1 ( ) 0 otherwise u u 1 if 1 ( ) 0 otherwise u u u 15 Parzen窗法 Parzen 估计量 pn(x) 是渐进无偏和平方误差一致 估计的限制条件: p(x) 在 x 点连续; 窗函数满足下列条件: 窗宽约束: || || 1 (1) 0; (2) 1; (3) sup ; (4) lim 0; d i i d u u u u u u u u (5) lim 0; (6) lim . n n n n V nV 16 Parzen窗法 窗宽 hn 的影响 hn 很大 δn 的强度低;且距离点 x 远近不同 的样本的 δn 相差不大 pn(x) 是 n 个宽度较 大且变化缓慢的函数的叠加,是平滑、低分辨力 的估计。 hn 很小 δn(x-xi) 的峰值大 pn(x) 是 n 个 以样本点为中心的尖脉冲的叠加,统计变动大, 是充满噪声的估计。 1 () ; n V h n n x x 1 1 () ; n n ni i p n x xx 17 Parzen窗法 窗宽 hn 是平滑参数,需优化,根据样本的数量 选择。 18 Parzen窗法 例1 :p(x) 和 均是正态分布 ( ) u 2 2 1 1 ( ) ~ (0,1); 1 () ; 2 ; 1 1 () . u n n i n i n n px N u e hhn x x p x nh h

20 Parzen窗法 Parzen窗法 口例2:(u)是正态分布 口例3:px)是一个均匀分布和一个三角形分布的 混合分布,(u)是正态分布。 te) h=0.2 A h=0.08 h=0.0 -AA IAn A - IAL IAI 22 Parzen?窗法 kn-近邻法 口讨论 口基本思想:把窗扩大到刚好覆盖k,个点:落在 窗内的样本点的数目固定,窗宽是变化的:即固 Smallh 定k(根据样本总数n选择),改变'。 is better in upper size depends on density region. Largeh in lower ○○⊙ Region. k.-近邻法 kn-近邻法 口概率密度估计表达式: 口例 P.(x)=kIn V 口收敛的限制条件: k=k√n lim=0: limk,=o; 口k的选择 ·当样本有限时,k将影响估计的平滑程度: ·当n一∞时,P(x)将收敛于px)
19 Parzen窗法 例2 : 是正态分布 ( ) u 20 Parzen窗法 例3:p(x) 是一个均匀分布和一个三角形分布的 混合分布, 是正态分布。 ( ) u 21 Parzen窗法 讨论 22 kn-近邻法 基本思想:把窗扩大到刚好覆盖 kn 个点;落在 窗内的样本点的数目固定,窗宽是变化的;即固 定 kn (根据样本总数 n 选择),改变 Vn size depends on density 23 kn-近邻法 概率密度估计表达式: 收敛的限制条件: kn 的选择 当样本有限时, kn 将影响估计的平滑程度; 当 n→∞ 时,pn(x) 将收敛于 p(x)。 / () ; n n n k n p V x lim 0; lim ; lim 0. n n n nn n k V k n 24 kn-近邻法 例 n 1 k kn
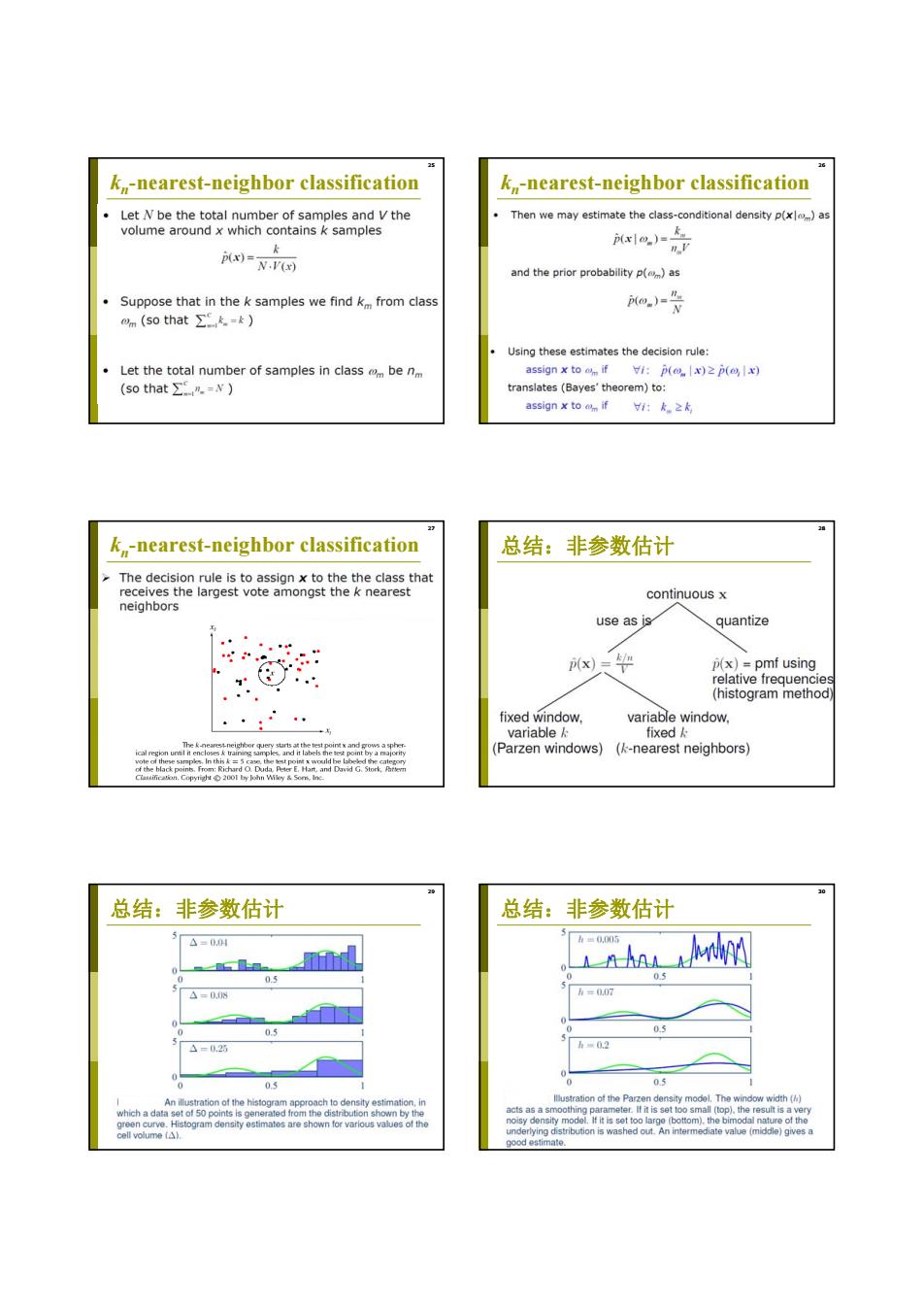
16 k-nearest-neighbor classification k-nearest-neighbor classification Let N be the total number of samples and V the Then we may estimate the class-conditional density p(xl)as volume around x which contains k samples pxlo.)-k p(x)=N.V() and the prior probability p()as Suppose that in the k samples we find k from class -是 omn(so that∑k.=k) Using these estimates the decision rule: Let the total number of samples in classm be nm assign x toom if :p(x)≥(间) (so that∑CR=v) translates (Bayes'theorem)to: assign x tom if:k.≥k k,-nearest-neighbor classification 总结:非参数估计 The decision rule is to assign x to the the class that receives the largest vote amongst the k nearest continuous x neighbors use as is quantize x)天 (x)=pmf using relative frequencie (histogram method fixed window, variable window. variable k: fixed nunhe (Parzen windows)(-nearest neighbors) 总结:非参数估计 总结:非参数估计 △=0.04 nhar nd h■0.005 0.5 0.5 △=0.08 h=0.07 0.5 03 △=0.25 0 0.5 0.5 An illustration of the histogram approach to density estimation.in llustration of the Parzen density model.The window width ( which a data set of 50 points is generated from the distribution shown by the acts as a sm tet,tis set to green curve.Histogram density estimates are shown for various values of the onis washgermediate value (middle/ee de I it is set tog cell volume (A). imate
25 kn-nearest-neighbor classification 26 kn-nearest-neighbor classification 27 kn-nearest-neighbor classification 28 总结:非参数估计 29 总结:非参数估计 30 总结:非参数估计

12 总结:非参数估计 总结:概率密度函数的估计方法 冠 Density Estimation 0.5 Parametric Non-parametric Semi-parametric 03 =0 0.5 ·K- 自 lllustration of the &nearest neighbor density model.The oarameter goverrts the dearee of smcoth A small value of(top)leads to a very density model.A large value (bottom)smoothes out the bimodal nature of the true distributon 讨论 口概率密度函数包含随机变量的全部信息,是导 致估计困难的重要原因。 口高维概率分布的估计无论在理论上还是实际操 作中都是十分困难的问题。 口进行模式识别并不需要利用概率密度的所有信 息,只需要求出分类面。 口先估计概率密度,再进行分类,可能走“弯 路
31 总结:非参数估计 32 总结:概率密度函数的估计方法 33 讨论 概率密度函数包含随机变量的全部信息,是导 致估计困难的重要原因。 高维概率分布的估计无论在理论上还是实际操 作中都是十分困难的问题。 进行模式识别并不需要利用概率密度的所有信 息,只需要求出分类面。 先估计概率密度,再进行分类,可能走“弯 路