北京大学：《模式识别》课程教学资源（课件讲稿）线性判别函数（第四部分）

第四章 线性判别函数 2010-11-8

第四章 线性判别函数 2010-11-8

线性支持向量机 线性SVM

线性支持向量机 线性 SVM

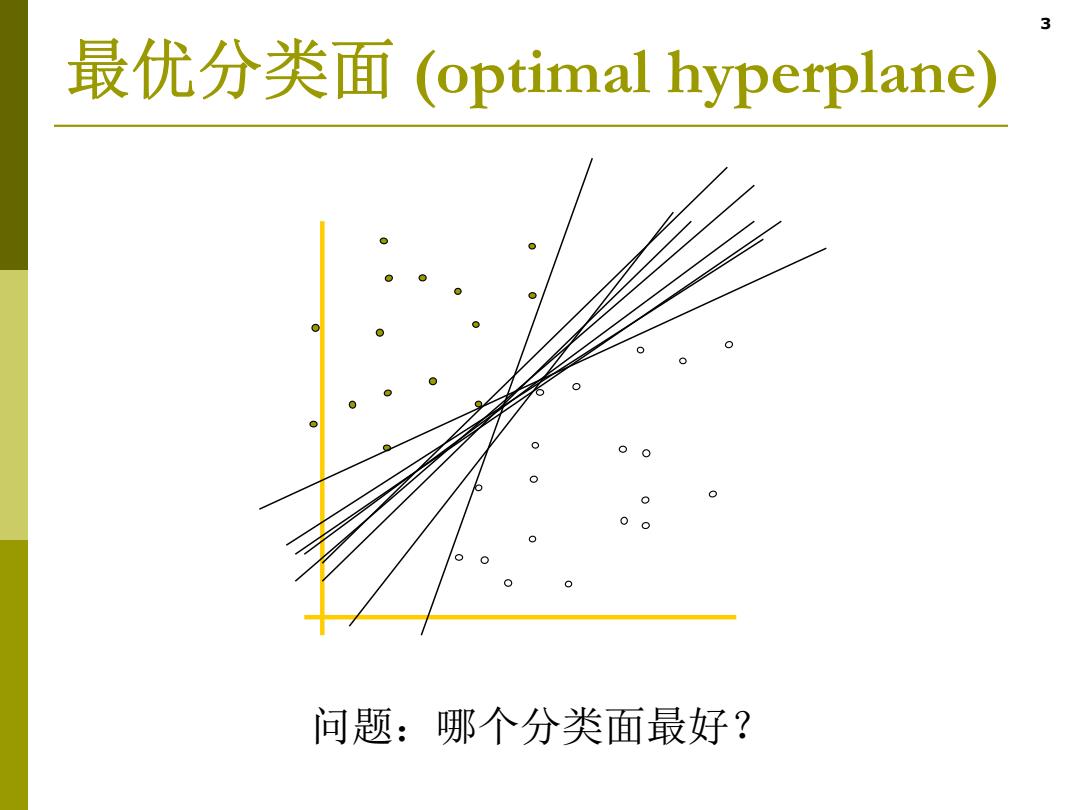
3 最优分类面(optimal hyperplane) 00 0 0 问题：哪个分类面最好？

3 最优分类面 (optimal hyperplane) 问题：哪个分类面最好？

最优分类面(optimal hyperplane) 支持向量 0 0 0 0 0 0 ● 0 边界距离(margin) 最优分类面

4 最优分类面 (optimal hyperplane) 边界距离（margin） 最优分类面 支持向量

5 最优分类面(optimal hyperplane) 口训练数据集合 (X1),(2,y2),…,(XN,yN), ∈，ye11y3 y,=1表示X,∈0 y,=-1表示X,∈02 口分类超平面 g(x)=w'·x+w0=0 wx+0=0; g(x) w 口决策函数 8(x)>0 f(x)=sgn(w2x+a） 8(x)<0

5 最优分类面 (optimal hyperplane)  训练数据集合  分类超平面  决策函数       11 2 2 1 2 , , , , , , , 1 , { 1,1} 1 N N i i d i i i i yy y y y y             xx x x x x  表示 ； 表示 0 0; T w x      0 ( ) sgn . T f x wx  

6 最优分类面(optimal hyperplane) 口样本x:到分类超平面的距离须满足 y8≥b>0; wIl 口问题：分类超平面的参数可增大或缩小任意正的 尺度而不影响分类结果→无数多解。 解决方案：可将距离分类面最近样本的决策函数 值归一化，即 g(x)1(where=)

6 最优分类面 (optimal hyperplane)  样本 xi 到分类超平面的距离须满足  问题：分类超平面的参数可增大或缩小任意正的 尺度而不影响分类结果  无数多解。  解决方案：可将距离分类面最近样本的决策函数 值归一化，即 ( ) 0; || || i i y g   b x w 1 ( ) 1, 1, , (where ). || || i i yg i N b x   w 

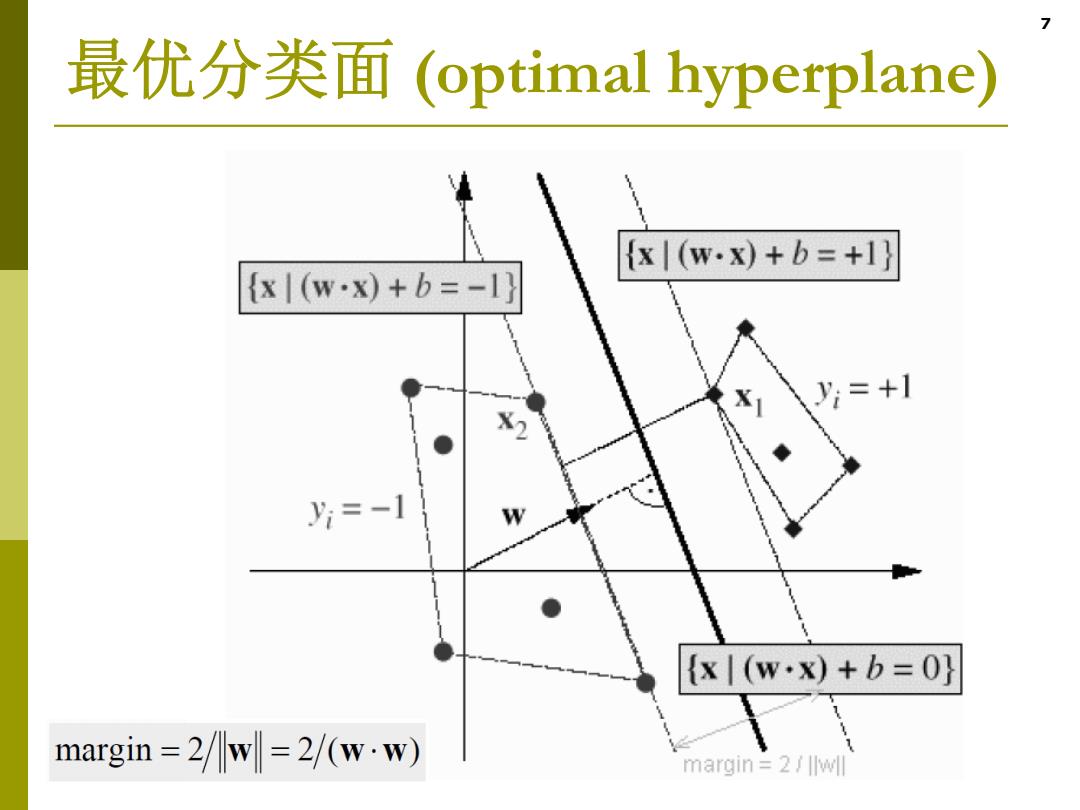
最优分类面(optimal hyperplane) {x|(wx)+b=+1} {x|(wx)+b=-1} y:=+1 片=-1 {x(w·x)+b=0} margin=2/w=2/(w·w) margin 2/wl

7 最优分类面 (optimal hyperplane)

9 线性可分时最优分类面的求解 Primal form: maximize margin → s.t. correct classification → y(wX+0)≥1，i=1,…,N; L(w,0,a）=wP-之a[(wx+o@,)-.a≥0， we seek to minimize L()w.r.t w and @ maximize L()w.r.t.a,;

9 线性可分时最优分类面的求解 2 0 : 1 maximize margin min ; 2 . . correct classificat Primal form ion ( ) 1, 1, , ; T i i s t y iN      w w x  2 0 0 1 0 1 (, ,) || || [ ( ) 1], 0; 2 we seek to minimize () w.r.t and ; maximize () w.r.t. ; N T ii i i i i L y L L               w w wx  w

10 线性可分时最优分类面的求解 ▣KKT条件 w①-w-立ayx=0w-ax Ow" i=l i=l 2. 0(w,-2gy=0, 0@,* i=1 3.y,(w*x,+0)-1≥0，i=1,…,N 4. 0*≥0，i, 5. a(y(wx,+@")-1=0,i

10 线性可分时最优分类面的求解  KKT 条件   0 1 1 0 0 1 0 0 (, ,) 1. 0 ; (, ,) 2. 0; 3. ( ) 1 0, 1, , ; 4. 0, ; 5. ( ) 1 0, . N N i ii i ii i i N i i i T i i i T ii i L y y L y y iN i y i                                                    w w xw x w w w x w x 

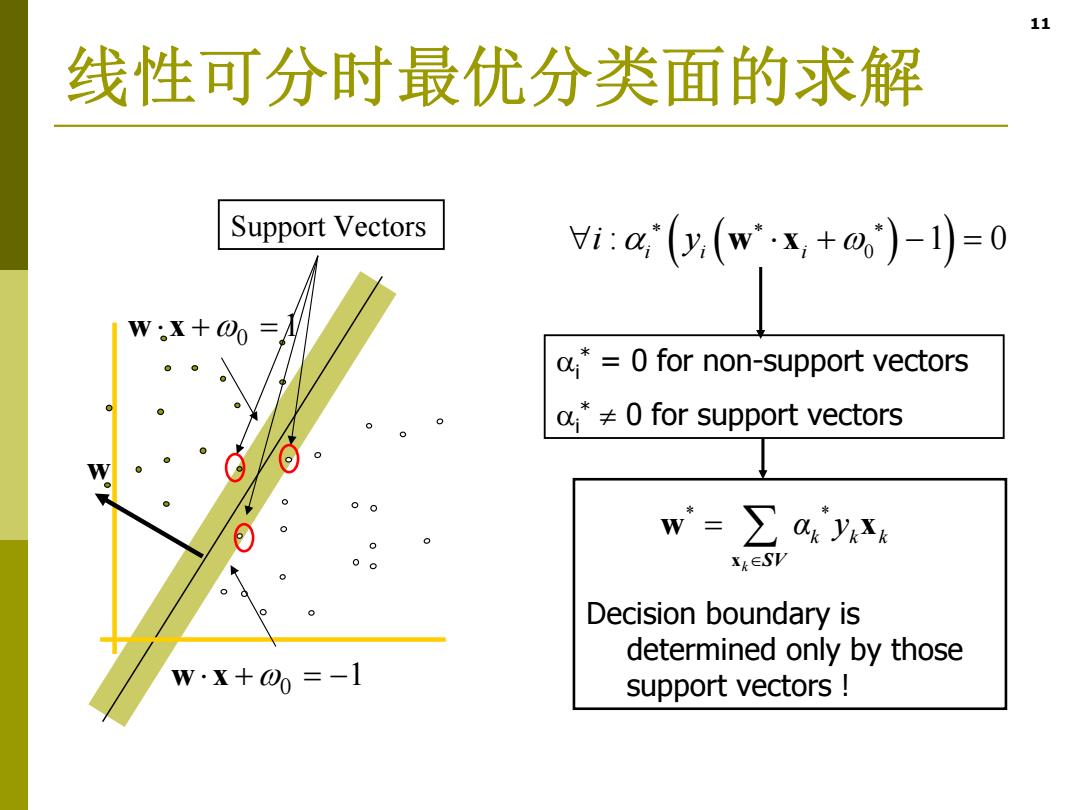
11 线性可分时最优分类面的求解 Support Vectors i:a(y(wx,+®）-1=0 wX+00 a*=0 for non-support vectors 0 for support vectors 0 w=∑aAy 0 Xk∈SV Decision boundary is determined only by those W·X+00=-1 support vectors

11 线性可分时最优分类面的求解 Decision boundary is determined only by those support vectors ! * * k αk kk y    x w x SV : 1   0   0 ii i i y      w x  i* = 0 for non-support vectors i*  0 for support vectors Support Vectors w 0 w x    1 0 w x    1