
数学摸型建立之一 一、 模型的整体设计户 二、合理假设
一、模型的整体设计 二、合理假设 数学模型建立之一

模型建立与建模目的密切相关 讲义3.5建立数学模型 几类常见建模目的: 纲举目张 1.描述或解释现实世界的各类现象。 2.预测感兴趣的事件是否会发生,或预测事物的发 展趋势. 3.优化管理、决策或者控制事物对象
模型建立与建模目的密切相关 几类常见建模目的: 1. 描述 或解释现实世界的各类现象. 2. 预测感兴趣的事件是否会发生,或预测事物的发 展趋势. 3. 优化管理、决策或者控制事物对象 讲义3.5 建立数学模型 纲举目张

模型的整体设计 时刻 建模过程中的几个环节 建斑 合理的假设 目的 建立数学结构 建立数学表达式
建模过程中的几个环节 模型的整体设计 合理的假设 建立数学表达式 建立数学结构 时刻牢记建模目的
一、模型的整体设计 讲义3.5.2模型的整体设计 数学模型的建立需同时描述出有关因素 之间的结构关系和数量关系 应清楚变量、变量之间关系在建模中的地位和作用. 城镇供水系统讲义例3.5.6城镇供水系统 考虑一个简化的城镇供水系统,水是由水库经由管道 流入水箱,再由水箱向各用户供水
数学模型的建立需同时描述出有关因素 之间的结构关系 和数量关系 应清楚变量、变量之间关系在建模中的地位 和作用. 城镇供水系统 考虑一个简化的城镇供水系统, 水是由水库经由管道 流入水箱 ,再由水箱向各用户供水 . 一、模型的整体设计 讲义 3.5.2 模型的整体设计 讲义例 3.5.6 城镇供水系统
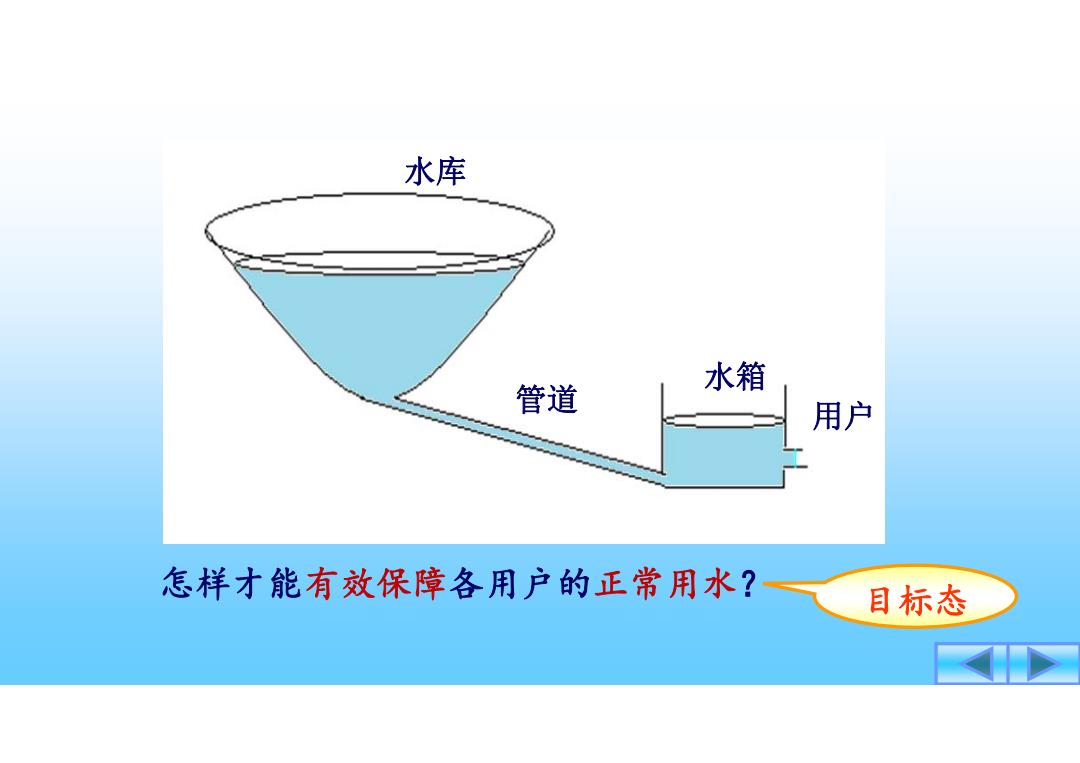
水库 管道 水箱 用户 怎样才能有效保障各用户的正常用水? 目标态
怎样才能有效保障各用户的正常用水? 目标态 水库 管道 水箱 用户
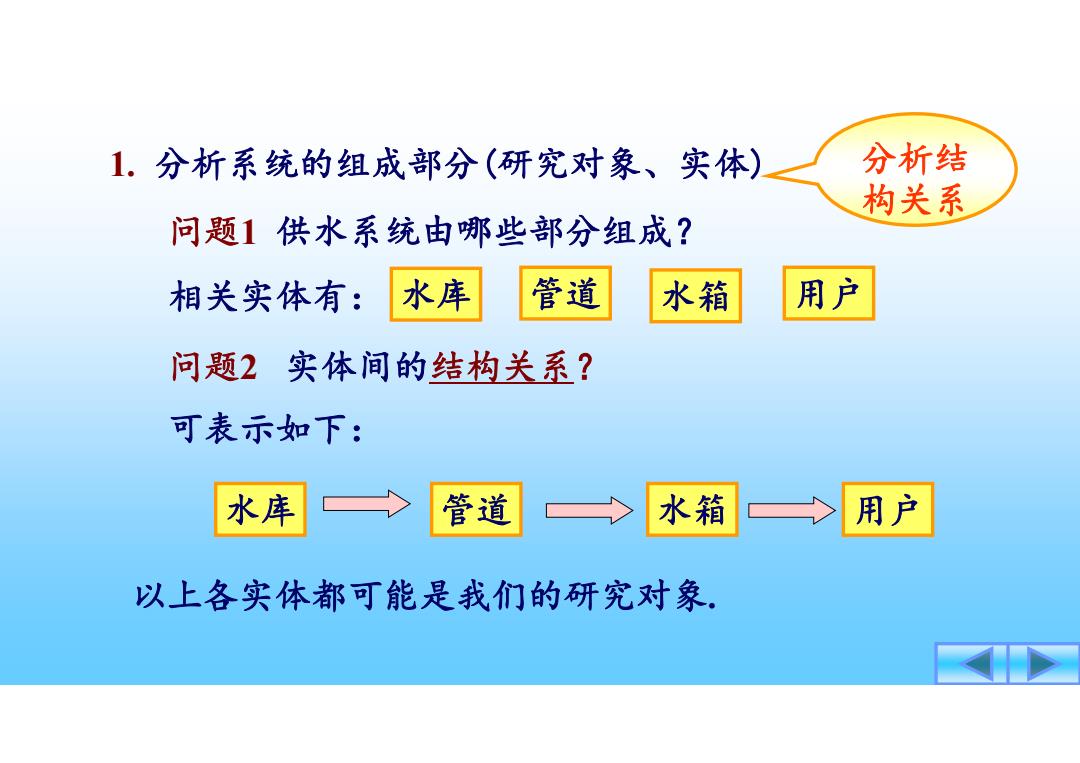
1.分析系统的组成部分(研究对象、实体) 分析结 构关系 问题1供水系统由哪些部分组成? 相关实体有: 水库 管道 水箱 用户 问题2实体间的结构关系? 可表示如下: 水库 管道 水箱 > 用户 以上各实体都可能是我们的研究对象
1. 分析系统的组成部分(研究对象、实体) 分析结 构关系 相关实体有: 问题1 供水系统由哪些部分组成? 可表示如下: 水库 管道 水箱 用户 问题2 实体间的结构关系? 以上各实体都可能是我们的研究对象. 水库 管道 水箱 用户

问题3分析各实体对供水产生影响的相关因素 水库 管道 水箱 用户 形状 直径 容积 用户数 容积 长度 横截面积 用水量 水深 两端高度差 水深 用水高峰 降雨量 水流量 出水管到水箱底的距离 用水低谷 江河注入量 通过出水口的水流量 蒸发和渗透 2.分析各实体间的关联关系,找出各实体的表征变量
问题3 分析各实体对供水产生影响的相关因素. 2. 分析各实体间的关联关系,找出各实体的表征变量. 水库 形状 容积 水深 降雨量 江河注入量 蒸发和渗透 管道 直径 长度 两端高度差 水流量 水箱 容积 横截面积 水深 出水管到水箱底的距离 通过出水口的水流量 用户 用户数 用水量 用水高峰 用水低谷
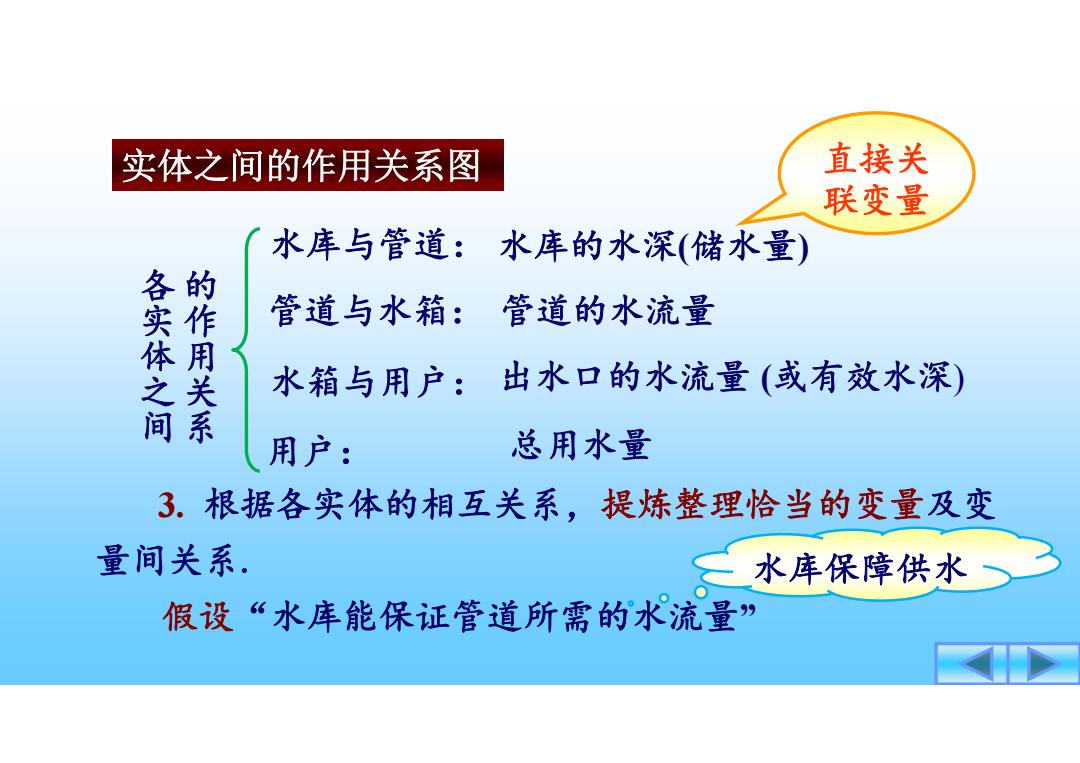
实体之间的作用关系图 直接关 联变量 水库与管道:水库的水深(储水量) 的 各实体之间 管道与水箱:管道的水流量 作用关系 水箱与用户:出水口的水流量(或有效水深) 用户: 总用水量 3。根据各实体的相互关系,提炼整理恰当的变量及变 量间关系, 水库保障供水 假设“水库能保证管道所需的水流量
实体之间的作用关系图 各实体之间 的作用关系 管道与水箱: 水库与管道: 水箱与用户: 水库的水深 (储水量 ) 管道的水流量 出水口的水流量 (或有效水深 ) 总用水量 3. 根据各实体的相互关系,提炼整理恰当的变量及变 量间关系. 假设“水库能保证管道所需的水流量 ” 直接关 联变量 用户: 水库保障供水

问题4需考虑关于各实体的哪些时间变量函数? *总用(需)水量D(): 设置 初态 *水箱的有效储水量Q(t)及2M=M心Q(); *管道能提供的供水量G()及GM=MxG(): 问题5各变量各有什么特征? 具有随机性 *用水量D()不可控,但可以对其记录、描述; *供水函数G(是可控变量. 主动设计描述 *水箱的有效储水量Q()呢? 保障供水的关健变量
设置 初态 * 总用(需)水量D(t); * 水箱的有效储水量Q(t)及 QM =Max Q(t) ; * 管道能提供的供水量G(t)及GM =Max G(t); 问题4 需考虑关于各实体的哪些时间变量函数? 问题5 各变量各有什么特征? * 用水量D(t)不可控,但可以对其记录、描述; * 供水函数G(t)是可控变量. 主动设计描述 具有随机性 * 水箱的有效储水量Q(t)呢? 保障供水的关键变量

明确需解决的问题选择供水函数G()以保证水箱 有效储水量函数Q()满足 2()≥D) 保障供水 问题6选用什么物理指标描述水箱储水量为佳? 估计水塔的水流量(AMCM-91A题):美国某州用 水管理机构要求各社区提供每天的总用水量,但许多社 区没有测量流入和流出水塔的测量仪器,只能代之以每 小时测量的水塔水位高度,一个社区的记录数据如下
明确需解决的问题 选择供水函数G(t)以保证水箱 有效储水量函数Q(t)满足 Q(t) ≥ D(t) 问题6 选用什么物理指标描述水箱储水量为佳? 估计水塔的水流量(AMCM-91A 题):美国某州用 水管理机构要求各社区提供每天的总用水量,但许多社 区没有测量流入和流出水塔的测量仪器,只能代之以每 小时测量的水塔水位高度,一个社区的记录数据如下 保障供水