
P放衣罗 情品课程 LIAOCHENG UNIVERSITY 第五节度量空间中的紧致性 厚德博学笃志精算 由于度量空间满足第一可数性公理,同时也是工空间,所 以一个度量空间是可数紧致空间当且仅当它是列紧空间.但 度量空间不一定是Lindel6f空间,所以从定理7.4.2并不能 断定列紧的度量空间是否一定就是紧致空间,本节研究这个 问题并给予肯定的回答 求实务实 踏实扎实英
第五节 度量空间中的紧致性 由于度量空间满足第一可数性公理,同时也是 T1 空间,所 以一个度量空间是可数紧致空间当且仅当它是列紧空间.但 度量空间不一定是 Lindelöff 空间,所以从定理 7.4.2 并不能 断定列紧的度量空间是否一定就是紧致空间.本节研究这个 问题并给予肯定的回答

P放大学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 定义7.5.1设A是度量空间(X,p)中的一个非空子集 集合A的直径diam(A)定义为 diam(A))= sup{p(x,y)x,y∈A 如果A是有界的 00 如果A是有界的 求实务实 踏实 扎实
定义 7.5.1 设 A是度量空间( , ) X 中的一个非空子集. 集合 A的直径diam A( )定义为 sup{ ( , ) , } A ( ) A x y x y A diam A = 如果 是有界的 如果 是有界的

P成术学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 定义7.5.2设(X,p)是一个度量空间,A是X的一个开覆盖, 实数2>0称为开覆盖A的一个Lebesgue数,如果对于X中的任何 一个子集A,只要diam(A)<入,则A包含于开覆盖A的某一个元 素之中 Lebesgue数不一定存在.例如考虑实数空间R的开覆盖 {o小aa1+aeZ 则任何一个正实数都不是它的Lebesgue数, 求实务实 踏实 扎实
定义 7.5.2 设( , ) X 是一个度量空间, 是 X 的一个开覆盖. 实数 0称为开覆盖 的一个 Lebesgue 数,如果对于 X 中的任何 一个子集 A ,只 要 diam A( ) ,则 A 包含于开覆盖 的某一个元 素之中. Lebesgue 数不一定存在.例如考虑实数空间 R 的开覆盖 1 1 ( ,1) ( , 1 ) | n n n Z n n + − − + + 则任何一个正实数都不是它的 Lebesgue 数

P成名学 情品课程 LIAOCHENG UNIVERSITY 定理7.5.1[Lebe sgue 数定理] 序列紧致的度量空间的每一 厚德博学笃志精算 个开覆盖有一个Lebesgue数, 定理7.5.5每一个序列紧张的度量空间都是紧致空间. 定理7.5.3设X是一个度量空间.则下列条件等价: (1)X是一个紧致空间: (2)X是一个列紧空间; (3)X是一个序列紧致空间: (④)X是一个可数紧致空间, 求实务实 踏实扎实
定理 7.5.5 每一个序列紧张的度量空间都是紧致空间. 定理 7.5.3 设 X 是一个度量空间.则下列条件等价: (1) X 是一个紧致空间; (2) X 是一个列紧空间; (3) X 是一个序列紧致空间; (4) X 是一个可数紧致空间. 定理 7.5.1 [Lebesgue 数定理] 序列紧致的度量空间的每一 个开覆盖有一个 Lebesgue 数
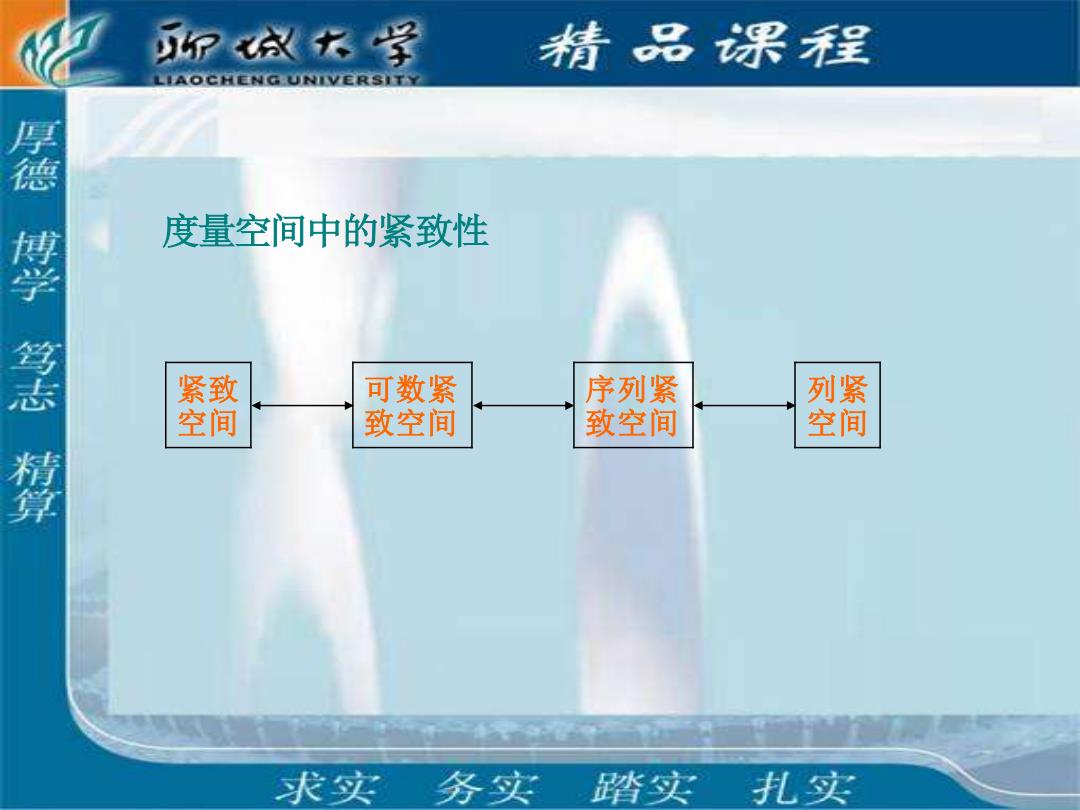
P放衣学 情品课程 LIAOCHENG UNIVERSITY 厚德博学驾志精算 度量空间中的紧致性 紧致 可数紧 序列紧 列紧 空间 致空间 致空间 空间 求实务实 踏实 扎实
度量空间中的紧致性 紧致 空间 可数紧 致空间 序列紧 致空间 列紧 空间