
§6.5分离性公理与子空间, (有限)积空间和商空间 定理6.5.1设X和Y是两个同胚的 拓扑空间.如果X是一个完全正则的 空间,则Y也是一个完全正则的空 间
§6.5 分离性公理与子空间, (有限) 积空间和商空间 定理6.5.1 设X和Y是两个同胚的 拓扑空间.如果X是一个完全正则的 空间,则Y也是一个完全正则的空 间.
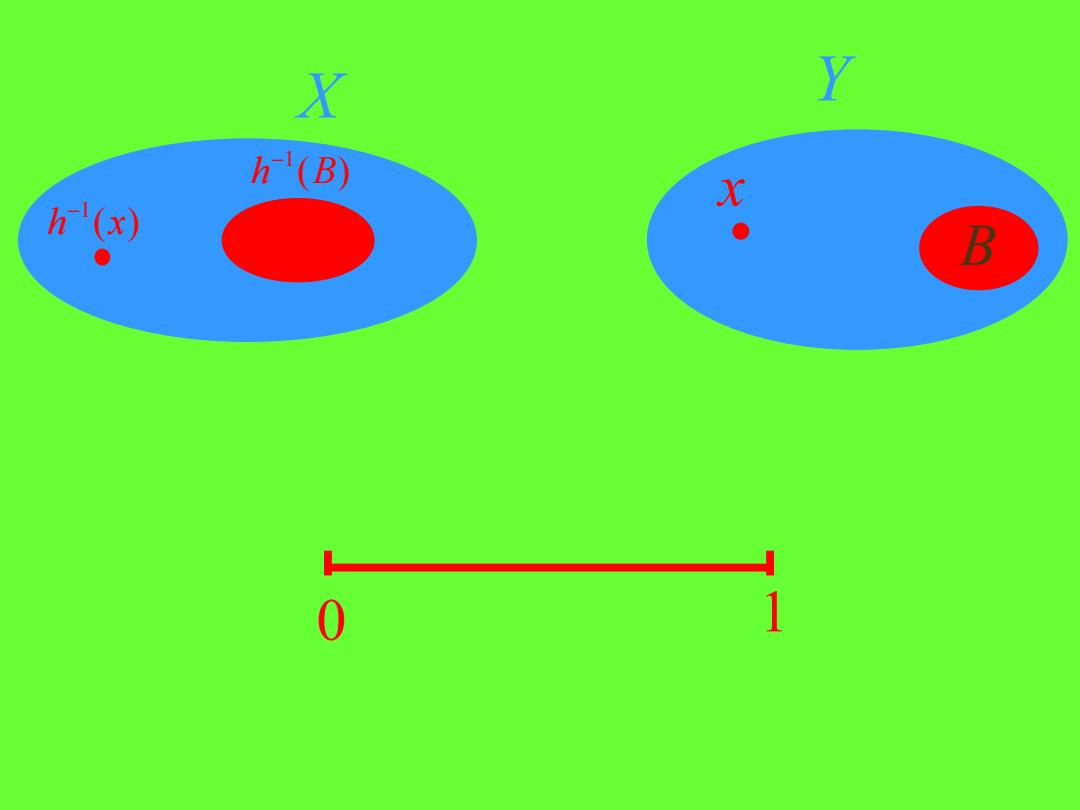
X Y h'(B) X h(x) B 0 1
X Y x B 0 1 1 h x( ) − 1 h B( ) −

证明设h:X→Y是一个同胚对于Y中的任意一个点x 和任何-个不包含点x的闭集B,k(x)和h(B)分别是X中 的-个点和一个不包含点h{x)的闭集由于X是一个完全正 则空间,故存在一个连续映射f:X→[0,1使得fh{x)》=0 和对于任何yE∫'(B)有f(y)=1.于是连续映射g=fch: Y-+[0,1]满足条件:gx)=0和对于任何z∈B有gz=1.1

定理65,2正则空间的每一个子空间都是正则空间 证朋设X是一个正则空间,Y是X的一个子空间.设y Y和B是Y的-个阔集使得y任B首先,在X中有-个闭集B 使得B∩Y=B因此y8.由于X是一个正则空间,所以y和 B分别在X中有开邻域(对于拓扑空间X雨)心和V使得U门 V=令U=U0Y和V=V∩Y,它们分别是y和B在子空 间Y中开邻域,此外易见U∩V=必.☐

引理6.54设肤射n[0,1→0,1定义为:对于任意1= (4,2)长0,12, m0)=max41,2 则m是一个连续映射

1 M(t,t) ●N4,t2) 0 1 {[0,a)a∈(0,1]}U{(b,1]b∈[0,1)} 1 1 a b 0 a b 1
0 1 1 1 2 M t t ( , )1 2 N t t ( , ) 0 a a b b 1 1 1 1

证明对于每-个a(0,1], m-'[0,a)=[0,a2 是[0,1中的-个开集;而对于每-个6E[0,1), m1([0,6])=[0,b12 是[0,1中的-个闭集,因此

第6,1=m[0,1-[0,1=[0,1-m[0,1) 是0,1中的-个开舆由于集族 =0,aa0,1U3,1[0,1明9 是0,1的-个子基放根定理2,65可见加是-个连续陕射
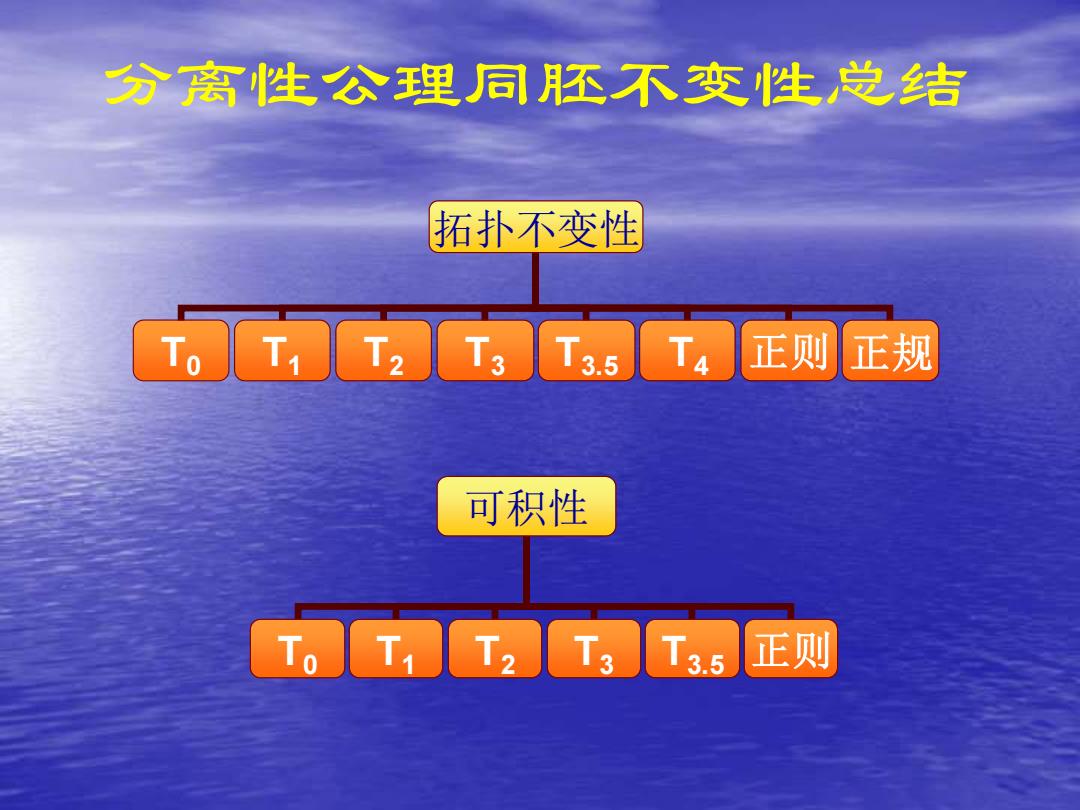
分离性公理同还不变性总结 拓扑不变性 ToT T2 T35 人 正则正规 可积性 To T1T2 T3 T3.5 正则
分离性公理同胚不变性总结 拓扑不变性 T0 T1 T2 T3 T3.5 T4 正则 正规 可积性 T0 T1 T2 T3 T3.5 正则
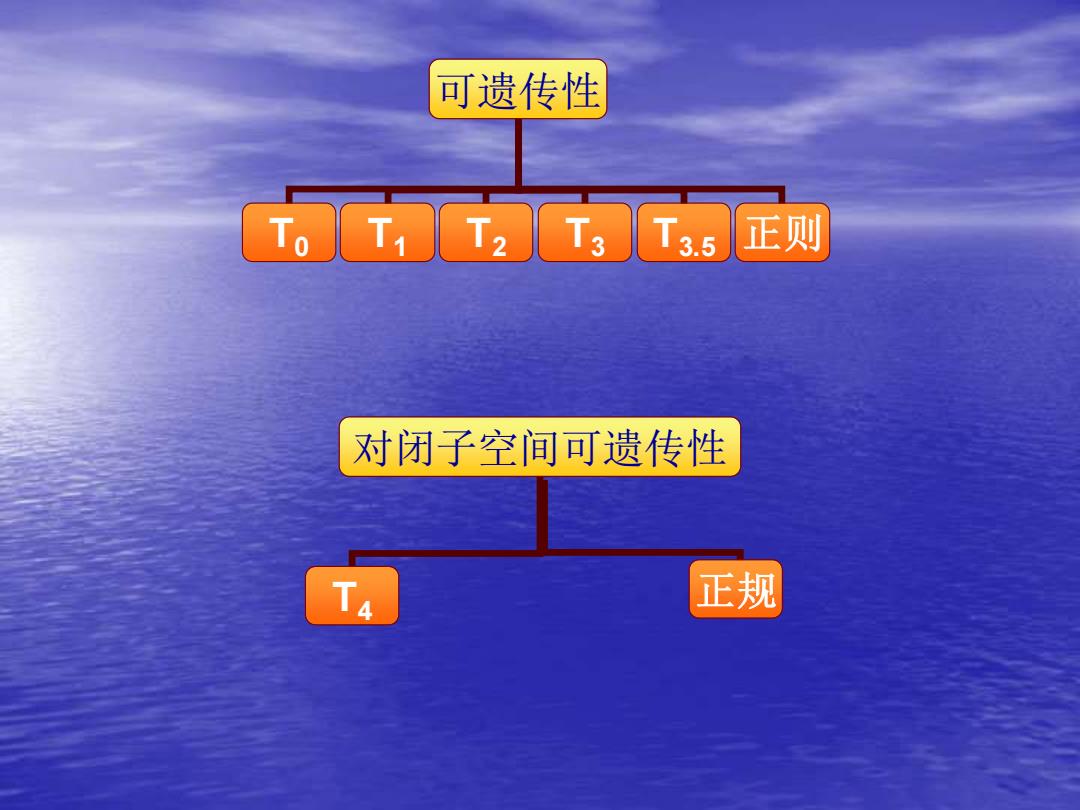
可遗传性 T。T1T2T3T35 正则 对闭子空间可遗传性 正规
可遗传性 T0 T1 T2 T3 T3.5 正则 对闭子空间可遗传性 T4 正规