
§6.3 Urysohn引理和Tietze扩张定理 定理6.3.1设X是一个拓扑空间, 是个闭区间,则X是一个正规空间 当且仅当对于X中的任意两个无交的 闭集A和B,存在一个连续映射 使得当X→[] 和兰f时=a x∈B f(x)=b
§ 6.3 Urysohn引理和Tietze扩张定理 定理6.3.1 设X是一个拓扑空间, 是一个闭区间,则X是一个正规空间 当且仅当对于X中的任意两个无交的 闭集A和B,存在一个连续映射 使得当 时 和当 时 [ , ] a bf X a b : [ , ] → x A x B f x a ( ) = f x b ( ) =

证明:充分性由于[a,b]≥[0,1],因此我 们只要证明[a,b]=[0,1]的情形即可. 必要性 设X是一个正规空间,A和B 是X的两个无交的闭集2,=Q⌒[0,] 2,={r(①),r(2),r(3)}不妨设r(1)=1和 r(2)=0 继续
证明:充分性 由于 ,因此我 们只要证明[a,b]=[0,1]的情形即可. 必要性 设X是一个正规空间,A和B 是X的两个无交的闭集, . 不妨设r(1)=1和 r(2)=0 [ , ] [0,1] a b 见下图 [0,1] Q Q I = { (1), (2), (3) } Q r r r I = 继续

X A B : 0 1 U
A B 0 1 f ] X

下面我们要做的工作是对每一个有理 数r(n)∈Q,对应着A的一个开邻域 U,,使得满足条件: (1)U,0=B; (2)若(n)<(m),则UcU,m. 接下来我就用归纳的方法定义A的 这些开邻域, 见下图
下面我们要做的工作是对每一个有理 数r(n)∈QI ,对应着A的一个开邻域 Ur(n),使得满足条件: (1) ; (2) 若 ,则 . 接下来我就用归纳的方法定义A的 这些开邻域: U B r(1) = r n r m ( ) ( ) U U r n r m ( ) ( ) − 见下图
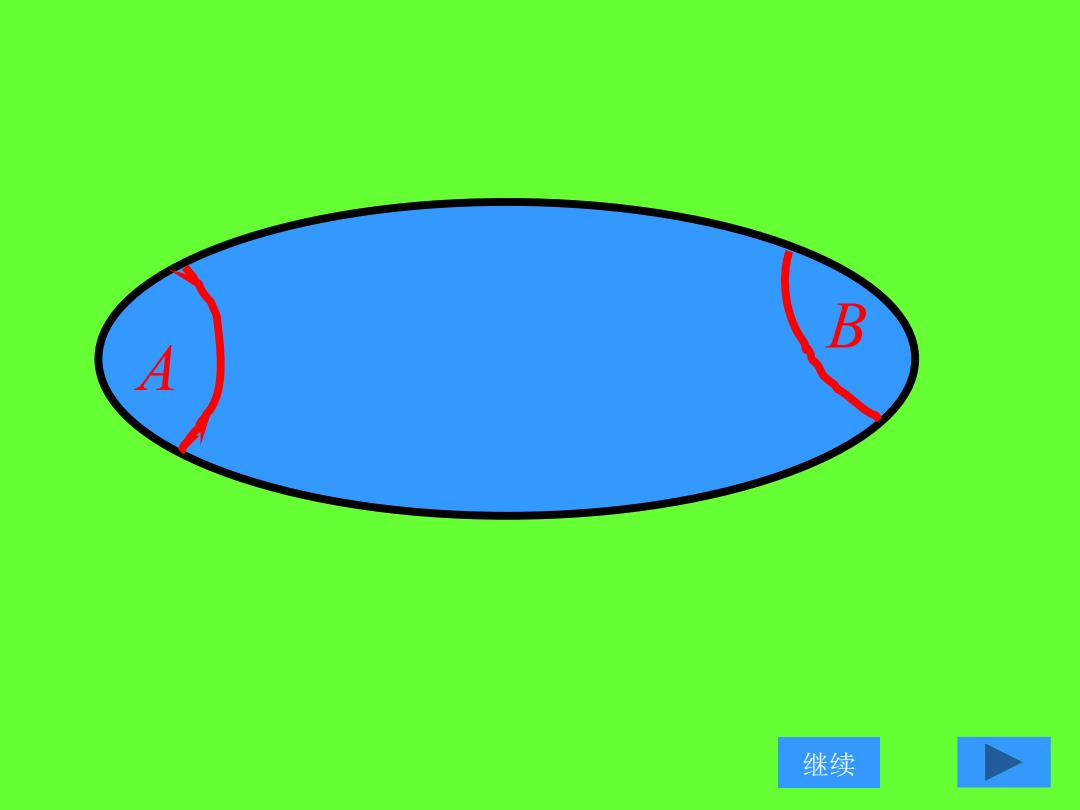
B A 继续
A B U 继续

取U,=B',U,,满足Ure EUro, 则 U,,U,2,满足(1)和(2),设对于n>2,A 的开邻域 乙Ur0,…,乙U,m-) 已经定义 令s=max r(i|r()r(n),i=1,…,n-1 见图
令 s r i r i r n i n = = − max{ ( }| ( ) ( ), 1, , 1} b r i r i r n i n = = − max{ ( }| ( ) ( ), 1, , 1} U B r(1) = U U r r (2) (1) − 取 , , 满足 , 则 满足(1)和(2),设对于n>2,A 的开邻域 已经定义. Ur(2) (1) (2) , U U r r (1) ( 1) , , U U r r n− 见图

由定理6.2.2, 选取Uro为U,的一 个开邻域使得Ur EU,从Uro的 取法可知A的者开邻域仍然满足条件 (1)和(2) 根据归纳原则,A的诸开邻域己经全 部定义,且满足条件(1)和(2) 见图
由定理6.2.2,选取Ur(n)为 的一 个开邻域使得 ,从 Ur(n)的 取法可知A的诸开邻域仍然满足条件 (1)和(2). 根据归纳原则,A的诸开邻域已经全 部定义,且满足条件(1)和(2). U U r n b ( ) − Us − 见图

定义映射:∫:X→[0,1] 使得对任意x∈X Jw=nire0xeC, 如果x廷B 如果x∈B 显然如果x∈A,则x∈U,2,所以 九x)=0;若x∈B,则x)=1
定义映射: 使得对任意 , f X: [0,1] → x X inf{ | } ( ) r r r Q x U x B f x x B = 如果 1 如果 显然如果 ,则 ,所以 f(x)=0 ;若 ,则 f(x)=1 . x A r(2) x U x B

下面证明f的连续性,我们知道 S={(a,+ola∈RU{-o,b)lb∈R 是实数空间R的一个子基,从而[0,1] 的一个子基为S=SIoW 则S=a,1ae0,)U0,b)b∈(0,U0,[0, 事实上S=S-{功,[0,1]还是[0,1]的 个子基
下面证明 f 的连续性,我们知道: 是实数空间R的一个子基,从而[0,1] 的一个子基为 则 事实上 还是[0,1]的一 个子基. S ={( , ) | } { , ) | } a a R b b R + − S S | 1 [0,1] = 1 S = {( ,1] | [0,1)} {[0, ) | (0,1]} { ,[0,1]} a a b b 1 S S= −{ ,[0,1]}

因此我们只需证明S的每一个元素 在f下的原象是开集就可以了. 即证对于任意a∈[0,1),-(a,1]) 是X中的开集: 对于任意b∈(0,1],(0,b]) 是X中的开集
因此我们只需证明 的每一个元素 在 f 下的原象是开集就可以了. •即证对于任意 , 是X中的开集; •对于任意 , 是X中的开集. S a[0,1) 1 f a (( ,1]) − b(0,1] 1 f b ((0, ]) −