
§7.2紧致性与分离性公理 定理7.2.1设X是一个 Hausdorff空间. 如果A是X的 个不包含点x的紧致子集,则点 x和紧致子集A分别有开邻域U 和V使得U∩V=p
§7.2 紧致性与分离性公理 定理7.2.1 设X是一个 Hausdörff空间. 如果A是X的一 个不包含点x的紧致子集,则点 x和紧致子集A分别有开邻域U 和V使得U∩V=
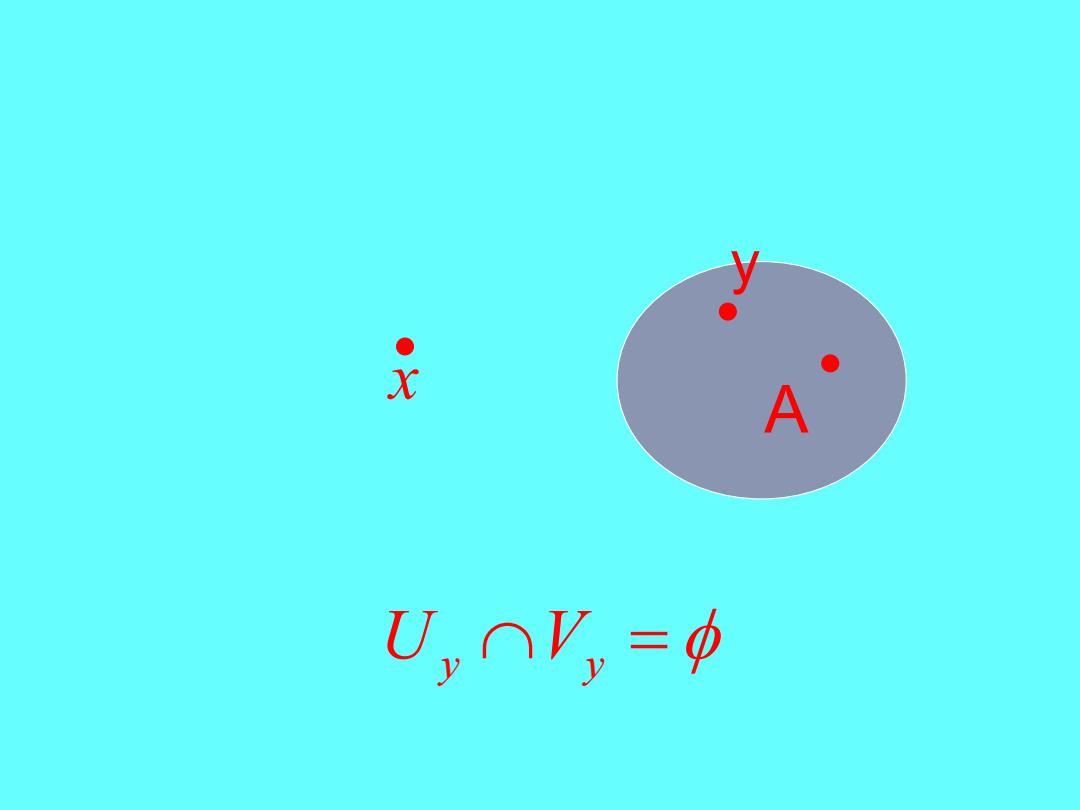
式 ● A U,ny=Φ
A x y U V y y =

证明设A是-个紧致子集EA,时于每-个A,由 于X是-个Hat空间,存在x的-个开域L,y的- 个牙郭浅,恨得,,=集族y湖显是案頸子 集A的-个开覆盖

它有-个有限子族,设为V,V2,,V 覆盖A.令U=∩U,和V=只,它们分别是点 和集合A的开邻域此外,由于对于每一个i=1,2,…,n有: onv,-C.nu.n-nu,nv,=8 所以 Unv-iUnv,)0(Un(

推论1.2,20间中的每-小紧致子美森灵闭美 证明设A是hs空润X的-个紧致子集,对于任有 X,知果xA,测限定理7,21可见z不是的凝豪点 因此凡A的餐案点都在A中,从而A是一个闭美

轮113在-个经效的Hac含间,-A集合是 集奶克处号终46灵-个餐威子集1

紧致子集和闭集的关系 紧致空间: Hausdorff:空间: 紧致Hausdorff空间:
紧致子集和闭集的关系 紧致空间: Hausdörff空间: 紧致Hausdörff空间:

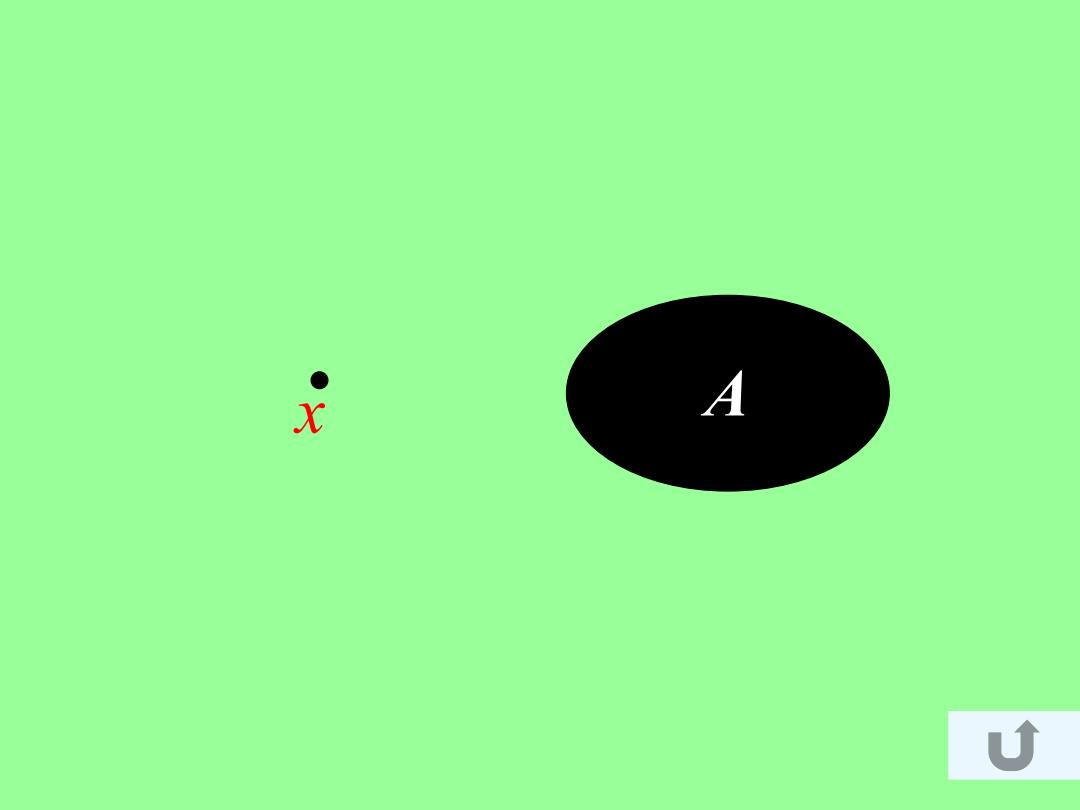
推论7,2,4每一个紧致的Hasdoff空间都是正则空间 证明设A是紧致的Hausdof空间X的个闭子集,x是 X中的-个不属于集合A的点.由于紧致空间中的闭子集是紧致 的(参见定理7,1.5),所以A是一个紧致子集.又根据定理 7,2.1,点x和集合A分别有开邻域U和V使得U门V=必.这 就证明了X是-个正则空间.· 图示
图示
U
x A

定理7.2.5设X是一个 Hausdorff:空间.如果A和B 是的两个无交的紧致子集, 则它们分别有开邻域和V使 得U∩V=
定理7.2.5 设X是一个 Hausdörff空间.如果A和B 是X的两个无交的紧致子集, 则它们分别有开邻域U和V使 得U∩V= .