
应用案例之一 案例一、 人▣变化规律预测 案例二、桌子能放稳吗?
应用案例之一 案例一、人口变化规律预测 案例二、桌子能放稳吗?

案例一人口变化规律预测 据人口学家们上世纪末预测,到2033年世界人口将突破 100亿,每年增加近1亿人口,以后还会迅猛增长.人们开始 考虑我们赖以生存的地球究竟是否能承受如此的增长 且全球各地区人口变化如下: 非洲地区人口将从10.33亿增至19.85亿; 欧洲人口将从7.33亿减至6.91亿. 增幅最大亚洲地区的人口将从41.67亿增至52.32亿;
据人口学家们上世纪末预测, 到2033年世界人口将突破 100 亿, 每年增加近 1亿人口, 以后还会迅猛增长. 人们开始 考虑我们赖以生存的地球究竟是否能承受如此的增长 . 案例一 人口变化规律预测 且全球各地区人口变化如下: 非洲地区人口将从10.33 亿增至19.85 亿 ; 欧洲人口将从7.33 亿减至6.91 亿 . 增幅最大亚洲地区的人口将从41.67 亿增至52.32 亿 ;

预测 地球究竟是香能系受如此的人口增长? 新冠肺病会全球扩散吗? 新冠肺病疫情的拐,点什么时间到来? 关注 中国人口将何变化7 全球疫情将如何变化? 共同特点 根据觉察到的目前情况及采取的调控措 施,预测将来的数量变化及后果
预测 地球究竟是否能承受如此的人口增长? 关注 中国人口将如何变化? 共同特点 新冠肺病会全球扩散吗? 全球疫情将如何变化? 根据觉察到的目前情况及采取的调控措 施,预测将来的数量变化及后果 . 新冠肺病疫情的拐点什么时间到来?

尝试建立数学模型预测中国人口数量变化. 1.问题前期分析 问题1影响t时刻某地区的人口总数变化的最显著因 素应包括哪些? Try! Try! Try! 2007A题:中国人口增长预测
尝试建立数学模型预测中国人口数量变化. 问题1 影响 t 时刻某地区的人口总数变化的最显著因 素应包括哪些? Try ! Try ! Try ! 1.问题前期分析 2007A题:中国人口增长预测
影响因素 个体的出生、 迁入迁出 性别比刚 年擀结构 教育程度 当地经济 生育观念 死七 问题2列举出的因素间有关联关系吗?哪些 因素最重要?
影响因素 个体的出生 、死亡 迁入 迁出 性别 年龄结构 比例 …… 教育程度 当地经济 生育观念 问题2 列举出的因素间有关联关系吗?哪些 因素最重要?

附录1《国家人口发展战略研究报告》 附录2人口数据及其说明(中的部分 数据)《中国人口统计年鉴》 问题3 通过阅读材料,你有什么体会想法? 问题4你们准备考虑哪些因素?将考虑哪些变量? Try Try! Try
问题3 通过阅读材料,你有什么体会想法? 附录1 《国家人口发展战略研究报告》 附录2 人口数据及其说明(中的部分 数据)《中国人口统计年鉴》 Try! Try! Try! 问题4 你们准备考虑哪些因素?将考虑哪些变量?

讨论最简单的情况,仅考虑出生和死亡对人口变化 的影响. 问题5用什么变量描述人口变化情况? 人口密度 人口总数 2.建立数学模型 设t时刻一个地区的人口总数为N() 问题6在时间段6,什△内出生和死亡所致人口数量 变化与哪些变量有关?
问题5 用什么变量描述人口变化情况? 讨论最简单的情况,仅考虑出生和死亡对人口变化 的影响. 人口密度 ? 人口总数 ? 设 t 时刻一个地区的人口总数为N(t) . 问题6 在时间段[t, t+ t] 内出生和死亡所致人口数量 变化与哪些变量有关? 2.建立数学模型

1)出生率和死亡率; 2) 初始时刻t=0时的人口基数; 3) 时间间隔△t的长短, 假设 时间间隔△t内的出生人数=bN(t)△t 时间间隔△t内的死亡人数=dN(t)△t 针对时间区间△t的两种情况进行讨论: (1)△t是一个确定的单位时间(比如△=1年) 令N=N(k)=N(k△),=1,2,3
3)时间间隔t 的长短. 2)初始时刻t = 0时 的人口基数; 1)出生率和死亡率; 假设 时间间隔t内的出生人数= b N(t)t 时间间隔t内的死亡人数=d N(t)t 针对时间区间t的两种情况进行讨论: (1)t是一个确定的单位时间(比如t=1年) 令 Nk= N(k)=N (k t), k=1,2,3,…

假定b>0,d>0,有 Nk1-N=(b-0Nkk=1,2,3.. (1) 人口改变量 得到关于人口序列N,=1,2,3,.的差分方程 Nk+1=(b-+1)Nkk=1,2,3,. (2) 根据上一年的人口数可推算出次年的人口数以及逐年 的人口数列
Nk+1 Nk = (b d) Nk k=1,2,3,… (1) 假定b>0, d > 0 , 有 人口改变量 得到关于人口序列Nk , k=1,2,3, …的差分方程 Nk+1= (bd+1)Nk k=1,2,3,… (2) 根据上一年的人口数可推算出次年的人口数以及逐年 的人口数列
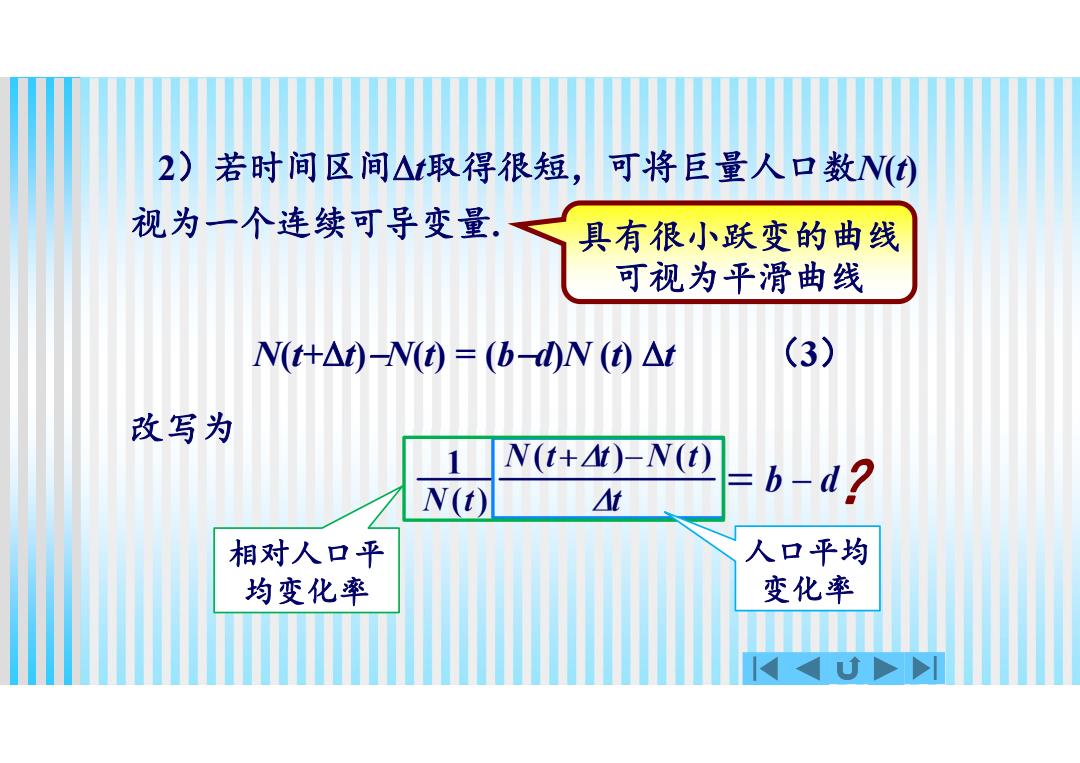
2) 若时间区间△r取得很短,可将巨量人口数N(心 视为一个连续可导变量。 具有很小跃变的曲线 可视为平滑曲线 Nt+△t)-N(t)=(b)N()△t (3) 改写为 N(t+f)-N(t) N(t) △t b-d? 相对人口平 人口平均 均变化率 变化率
2)若时间区间t取得很短,可将巨量人口数N(t) 视为一个连续可导变量. 具有很小跃变的曲线 可视为平滑曲线 N(t+t)N(t) = (bd)N (t) t (3) 改写为 人口平均 变化率 相对人口平 均变化率 ?