
模型的分析与评价 一、 模型及解的分析户 二、 模型误差分析
一、模型及解的分析 二、模型误差分析 模型的分析与评价
x1 实际问题分析 建立数学模型 可以交作 业了吗? 求解数学模型 老师的责 任与义务? 模型与模型解的分析及检验
求解数学模型 实际问题分析 建立数学模型 模型与模型解的分析及检验 可以交作 业了吗? 老师的责 任与义务? x1

一、 模型及解的分析 始于现实世界并终于现实世界 讲义3.7模型的分析和评价 数学建 最终要得到现 模工作 实问题的解签 建模的重要特征: 1)不明确性未设定需解决的具体问题和求解条件; 2)不唯一性方法不唯一,模型不唯一、正确解答不唯一;
始于现实世界并终于现实世界 数学建 模工作 最终要得到现 实问题的解答 一、模型及解的分析 建模的重要特征: 1) 不明确性 未设定需解决的具体问题和求解条件; 2) 不唯一性 方法不唯一,模型不唯一、正确解答不 唯一; 讲义3.7 模型的分析和评价

3)主观性描述实际研究对象其规律性带有较强的主观性; 4)试错性各个环节都是原创性工作,需要不断探索、试 错并纠错。 必需对模型及解 进行分析评价 问题1需要做哪些分析检验?如何做? 体重估算《格列佛游记》中小人国的小人们为估算格列 佛的食量,利用身体的相似性,建立了一个数学模型, W-a H3 W是人的体重,H是人的身高
体重估算《格列佛游记》中小人国的小人们为估算格列 佛的食量,利用身体的相似性,建立了一个数学模型. 3) 主观性 描述实际研究对象其规律性带有较强的主观性; 4) 试错性 各个环节都是原创性工作,需要不断探索、试 错并纠错. 必需对模型及解 进行分析评价 W= a H3 W是人的体重,H 是人的身高. 问题1 需要做哪些分析检验?如何做?

检验先确定参数,新生婴儿身长约50厘米,重约3 千克,代入模型得 a=W1H3=3/0.53=24, 建立模型为 W=24H3 据此可计算得 身高为1.5米的儿童体重为 W1.5)=81(千克); 身高为2米的运动员体重为W(2)=192(千克): 评价是适用于肥胖人群的体重一身高模型! 不适合一 般人群
检验 先确定参数a,新生婴儿身长约50厘米,重约3 千克,代入模型得 建立模型为 W=24H3 据此可计算得 / 3/ 0.5 24, 3 3 a W H 身高为1.5米的儿童体重为 W(1.5)=81(千克); 身高为2米的运动员体重为 W(2)=192(千克). 评价 是适用于肥胖人群的体重-身高模型! 不适合一 般人群

检验模型及其解是数学建模 因建模的主 工作的重要环节 观性,思考 不周的可能 性很大 问题2需要做哪些方面的检验及分析工作? 1)是否达到了建模目的?2)求得的解合乎实际吗? 3)模型的适用范围怎样?4)参数α的确定? 4)假设是否合理? 5)所建模型是否有原理性、知识性、常识性错误?
检验模型及其解是数学建模 工作的重要环节 因建模的主 观性,思考 不周的可能 性很大! 问题 2 需要做哪些方面的检验及分析工作? 2)求得的解合乎实际吗? 3)模型的适用范围怎样? 5)所建模型是否有原理性、知识性、常识性错误?…… 4)参数 a的确定? 4)假设是否合理? …… 1)是否达到了建模目的?

估算洞深(例3.7.2)将一块石头扔进洞中估算洞的深度. 从扔下石头至听到声音的时间t和洞深h的一个关系模型 0=是+-k-是,2 h一洞深,t一听到回声的时间. 用到假设: *1石头下降时所受空气的阻力和速度成正比; *2阻力产生的加速度和速度成正比. 其中比例系数均为k
估算洞深 (例3.7.2) 将一块石头扔进洞中估算洞的深度. 从扔下石头至听到声音的时间 t 和洞深 h 的一个关系模型 exp( )) , 0, 1 ( ) ( 2 t kg kt k t kg h t h — 洞深,t —听到回声的时间. 用到假设: *1 石头下降时所受空气的阻力和速度成正比; *2 阻力产生的加速度和速度成正比. 其中比例系数均为k


系列分析检验: 1.检查模型的量纲是否正确?讲义3.6.2模型求解基础 应用量纲齐次原则对数学模型和模型的解进行量纲 一致性检验. 量纲齐次原则:任一有意义的物理方程必定是量纲一 致的,即有 dim(左边)=dim(右边) 故等式左边和右边的每一项也都必须有相同的量纲,只有量 纲相同的项才可以相比较,相加减.在一个模型中的单位也必 须统一,否则整个建模工作都会失败
系列分析检验 : 1. 检查模型的量纲是否正确? 应用量纲齐次原则对数学模型和模型的解进行量纲 一致性检验. 讲义3.6.2 模型求解基础 量纲齐次原则: 任一有意义的物理方程必定是量纲一 致的, 即有 dim(左边)= dim(右边) 故等式左边和右边的每一项也都必须有相同的量纲,只有量 纲相同的项才可以相比较,相加减. 在一个模型中的单位也必 须统一,否则整个建模工作都会失败
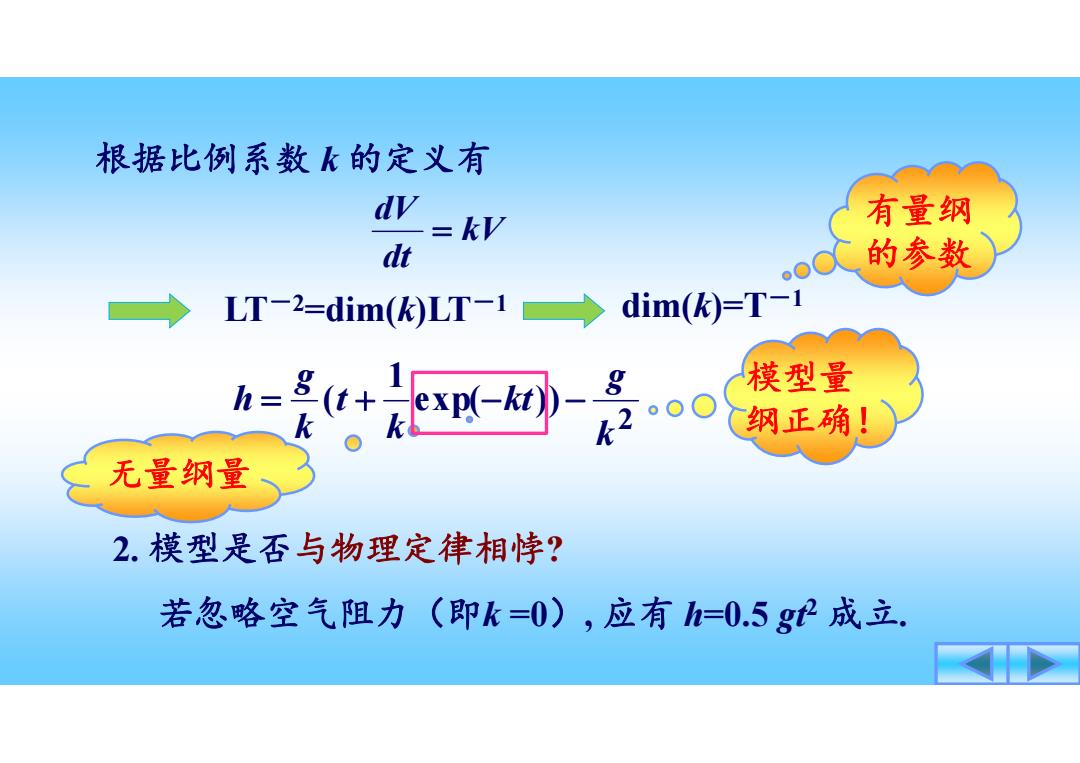
根据比例系数k的定义有 dy .=kV 有量纲 dt 的参数 LT-2=dim(k)LT-1→ dim(k)=T-1 e--是0 模型量 纲正确! 无量纲量 2.模型是否与物理定律相悖? 若忽略空气阻力(即k=0),应有h=0.5g成立
根据比例系数 k 的定义有 LT-2=dim(k)LT-1 dim(k)=T-1 kV dt dV 有量纲 的参数 2 exp( )) 1 ( kg kt k t kg h 无量纲量 模型量 纲正确! 2. 模型是否与物理定律相悖? 若忽略空气阻力(即k =0), 应有 h=0.5 gt2 成立