北京大学：《模式识别》课程教学资源（课件讲稿）特征的选择和提取（第二部分）

第七章 特征的选择与提取 2010-11-29

第七章 特征的选择与提取 2010-11-29

基于概率分布的可分性判据

基于概率分布的可分性判据

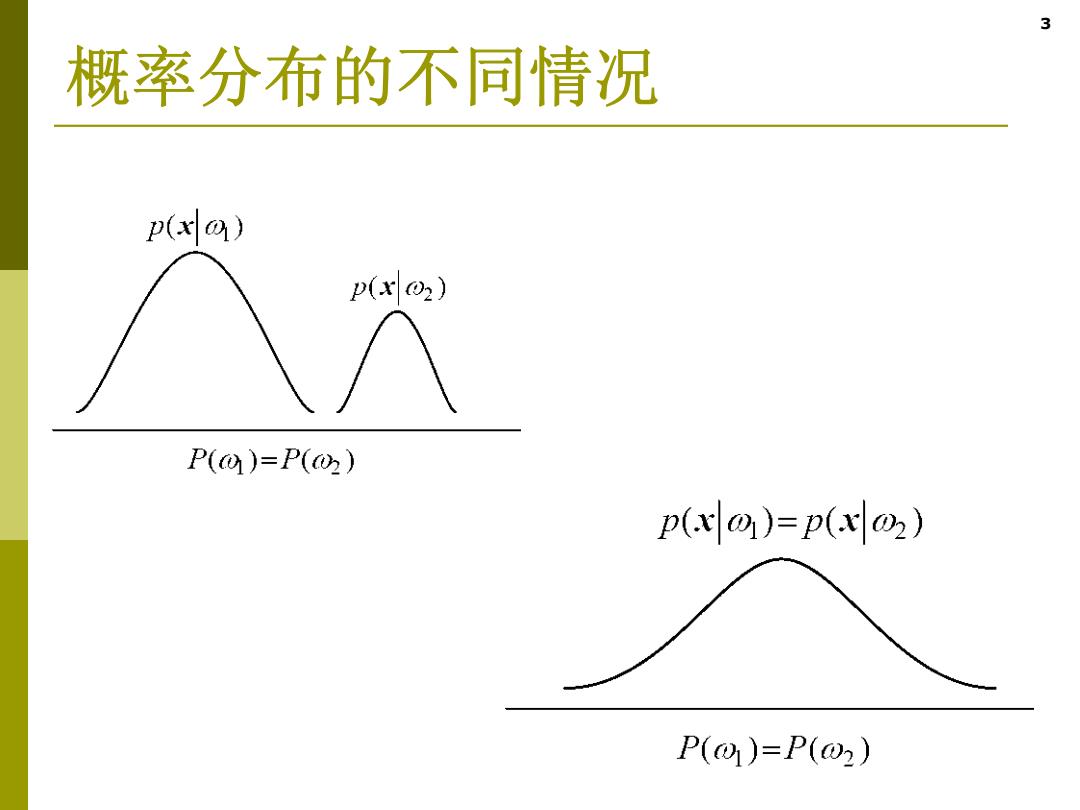
3 概率分布的不同情况 p(xa) p(x⊙2) P(0)=P() p(xo)=p(xo2） P()=P()

3 概率分布的不同情况

4 概率密度的距离 J()=Jg[p(xl@).p(xl@2).R.PJx 须满足的条件 1.,是非负，即J,≥0： 2. 当两类完全不交叠时，J,达到其最大值，即 if p(x)p(xl@2)=0,Vx,then J=J 3. 当两类分布密度相同时，J。=0: if p(xl@)=p(x|@2),Vx,then J=0

4 概率密度的距离 J ( ) ( | ), ( | ), ,   g p p PPd    1 2 12   xx x  须满足的条件 1. Jp 是非负，即 Jp ≥ 0； 2. 当两类完全不交叠时， Jp 达到其最大值，即 3. 当两类分布密度相同时， Jp ＝ 0； 1 2 m a x if ( | ) ( | ) 0, , then ; p p p xx x      J J 1 2 if ( | ) ( | ), , then 0. p pp J x xx     

5 Bhattacharyya距离 J:=-In[Ip(xl@)p(xl@2)]dx 1)两类完全重合时，J3=0; 2)两类完全不交叠时，J=∞； 3)与错误概率的上界有直接关系： 卫≤[P(@,)P(o2exp(-Ja)】

5 Bhattacharyya 距离 1) 两类完全重合时， JB = 0； 2) 两类完全不交叠时， JB =∞； 3) 与错误概率的上界有直接关系： 1/2 1 2 ln [ ( | ) ( | )] B J   pp d    xx x  1 2 1 2 ( ) ( ) exp( ). PP P J e B    

6 Chernoff界限 Jc=-lnp'(x@)p(x@,k,s∈[0,1： 1)for Vs∈[0,1]Jc≥0； Jc=0p(x @)=p(x @)Vx; 2)当x的各分量彼此独立时， Jc(sx,x,…,xn)=∑J(sx方 i= Jc(SX1,X2,…Xk)≤Jc(S,X1,X2,Xk,Xk+1)

6 Chernoff 界限 1 1 2 ln ( | ) ( | ) , [0,1]; s s C J p p ds        x xx 1 2 1 2 1 12 12 1 1) for [0,1] 0; 0 ( | ) ( | ), ; 2) ( ; , , , ) ( ; ); ( ; , , ) ( ; , , , ). C C n C n Ci i C k C kk s J Jp p J sx x x J sx J sx x x J sx x x x             x xx x    当 的各分量彼此独立时

7 散度 口对数似然比：1，(x)=In P(xo): p(x|@,) 口①，类和”，类的平均可分性信息 6=-xah照，1-印o训 口散度：区分“，类和ω，类的总的平均可分信息 Jo=I,+!,=J[p(x1@)-p(x1o P(x@ds: p(x@)

7 散度  对数似然比：  ωi 类和ωj 类的平均可分性信息  散度：区分ωi 类和ωj 类的总的平均可分信息 ( | ) ( ) ln ; ( | )i ij j p l p   x x x (| ) [ ( )] ( | )ln [ ( )]. (| )i ij ij i ji ji X j p I El p d I El p        x xx x x x ， ( | ) [ ( | ) ( | )]ln ; ( | )i D ij ji i j X j p J II p p d p         x xx x x

8 正态分布下的散度 is到a)2产wt---u J。=,2,+y-2川 +②+X,g, 如果两类协方差矩阵相等，则 JD=(,-,)'Σ'(4，-)=JM

8 正态分布下的散度 1 /2 1/2 1 1 ( | ) exp[ ( ) ( )] (2 ) | | 2 T i ii i d i p    x x     μ Σ x μ Σ ； 1 1 1 1 1 [ 2] 2 1 ( ) ( )( ); 2 D i j ji T i j i j i j J tr          ΣΣ ΣΣ I μμ Σ Σ μμ 1 ( )( ) ; T D ij ij M J J     μ μ Σμ μ 如果两类协方差矩阵相等，则

9 正态分布下的Bhattacharyyal距离 -）俱- nl②，+四)/2 2 2,, 如果两类协方差矩阵相等，则有 8JB=(u,-,)）∑(，-)=JD=JM

9 正态分布下的Bhattacharyya距离 1 1/2 1 () () 8 2 1 |( )/2| ln ; 2 | || | T i j B i j i j i j i j J                 Σ Σ μμ μ μ Σ Σ Σ Σ 1 8 ( )( ) . T B ij ij DM J J J     μ μ Σμ μ 如果两类协方差矩阵相等，则有

10 基于概率距离判据的特征提取 两类别问题，正态分布及相同的协方差矩阵 J=(41-2)YΣ'(1-2)=r2'(1-21-2)/ =r[ΣM(其中，M=(-241-2))月 a-z4'Aa→其有非奇#安换不安性 (A)--A(AA)(AMA)(AEA)2MA(AA)-0 aA MA-EA(AEA)(A'MA=0:

10 基于概率距离判据的特征提取  两类别问题，正态分布及相同的协方差矩阵   1 1 1 2 1 2 1 21 2 1 1 21 2 ( ) ( ) ( )( ) ( )( ) T T D T J tr tr                   μ μ Σμ μ Σμ μμ μ Σ M M 其中， ； μμμμ   1 ( ) D D T T J tr J            A A ΣA A MA 具有非奇异变换不变性           1 11 1 ( ) 2 20 0; D T TT T T T J            A ΣA A ΣA A MA A ΣA MA A Σ A A MA ΣA A ΣA A MA