
第六章近邻法 2010-11-15
第六章 近邻法 2010-11-15

最近邻法 Nearest Neighborhood Classifier
最近邻法 Nearest Neighborhood Classifier
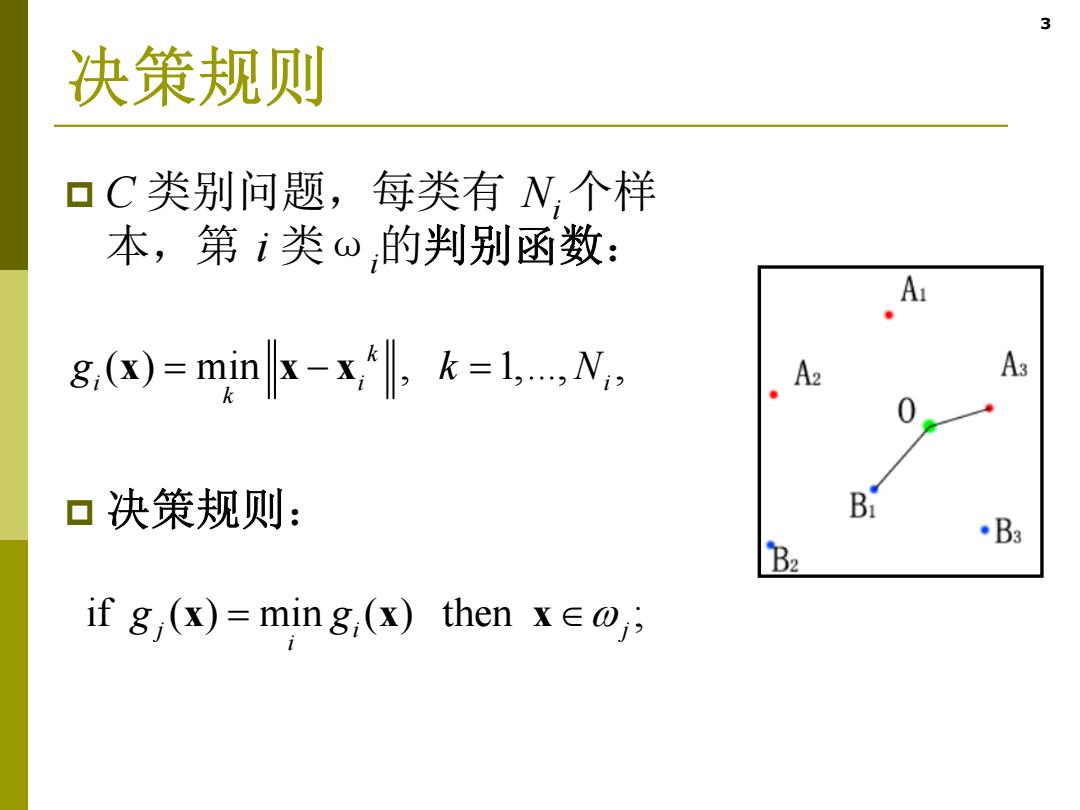
3 决策规则 口C类别问题,每类有N,个样 本,第i类ω的判别函数: A g.(x)=min=1....N. A2 A3 口决策规则: B ·B3 B2 if g (x)=ming,(x)then xe
3 决策规则 C 类别问题,每类有 Ni 个样 本,第 i 类ωi 的判别函数: 决策规则: ( ) min , 1,..., , k i ii k g k x xx N if ( ) min ( ) then ; j i j i g g x xx
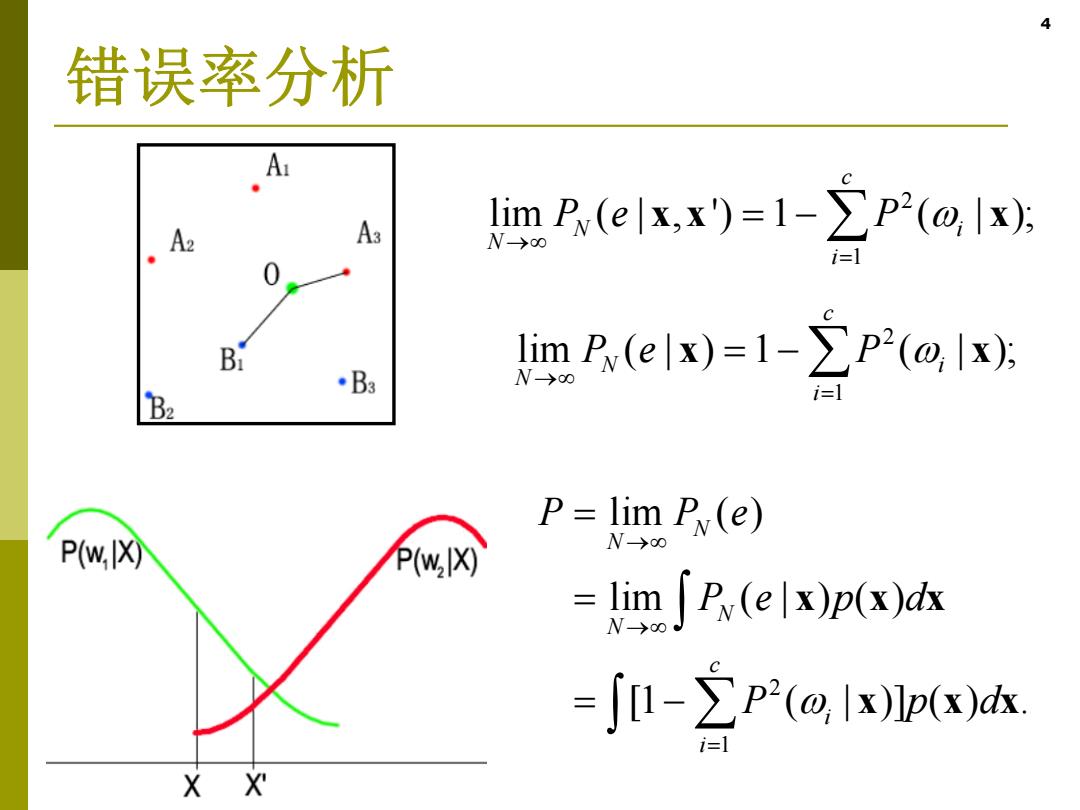
4 错误率分析 A2 A3 lim Py(elx,x)=1->P2(@.lx) N。 Bi lim Py(elx)=1->P-(@.lx) ·B3 B2 P=lim Py(e) P(w,lX) N->oo Pw,X闪 =lim∫P,(ex)p(x)dk =J[1-∑p2(@,xp(x)k. X X
4 错误率分析 2 1 lim ( | )1 ( | ); c N i N i Pe P x x 2 1 lim ( | , ') 1 ( | ); c N i N i P e P x x x 2 1 lim ( ) lim ( | ) ( ) [1 ( | )] ( ) . N N N N c i i P Pe Pe p d P pd x xx x xx
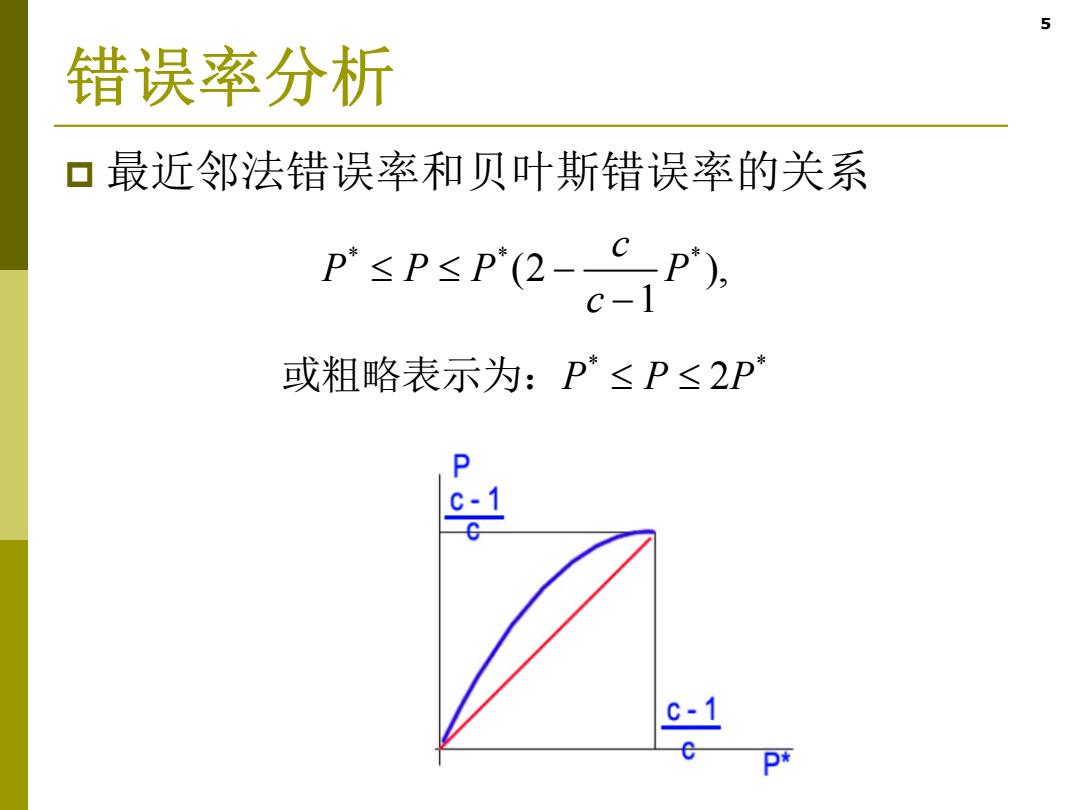
5 错误率分析 口最近邻法错误率和贝叶斯错误率的关系 PspsPQ-eP) 或粗略表示为:P*≤P≤2P c-1
5 错误率分析 最近邻法错误率和贝叶斯错误率的关系 ** * * * (2 ), 1 2 c P PP P c PPP 或粗略表示为:

k-近邻法
k-近邻法
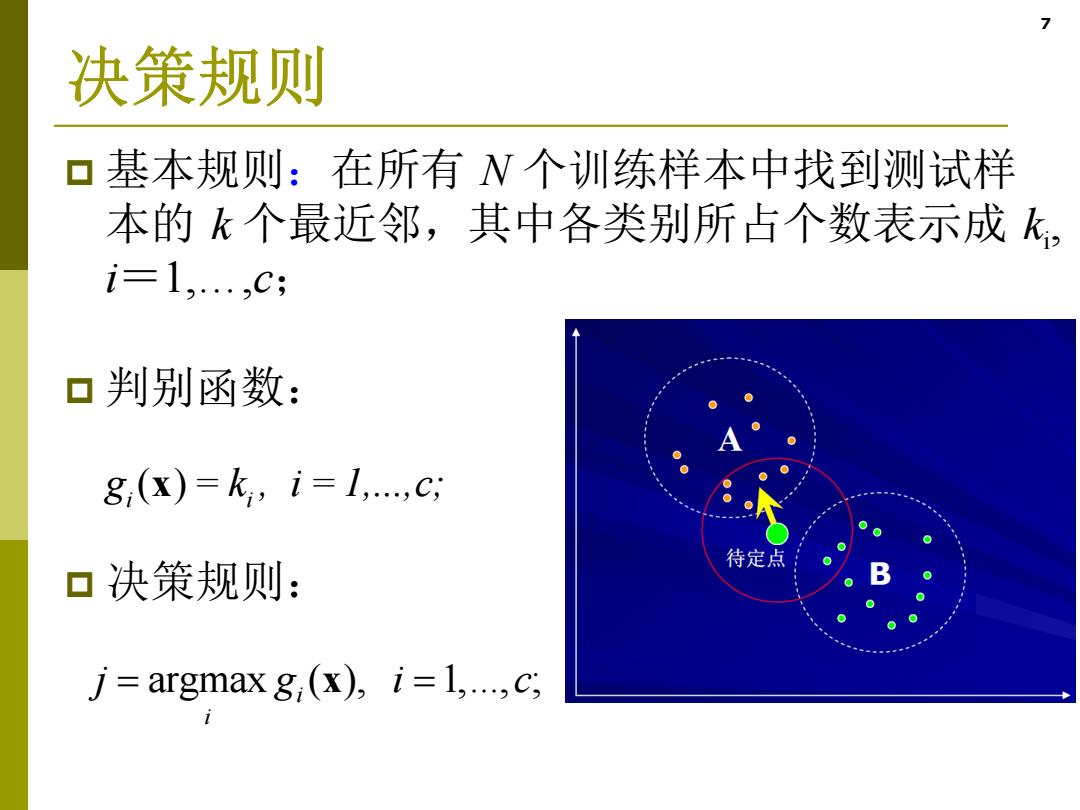
7 决策规则 基本规则:在所有N个训练样本中找到测试样 本的k个最近邻,其中各类别所占个数表示成k, i=1,…,C 口判别函数: 8(X)=k,i=1,,C, 待定点 口决策规则: j=argmax g(x),i=1,...,c;
7 决策规则 基本规则:在所有 N 个训练样本中找到测试样 本的 k 个最近邻,其中各类别所占个数表示成 ki , i=1,…,c; 判别函数: 决策规则: argmax ( ), 1,..., ; i i j gi c x ( ) i i g x = k , i = 1,...,c;
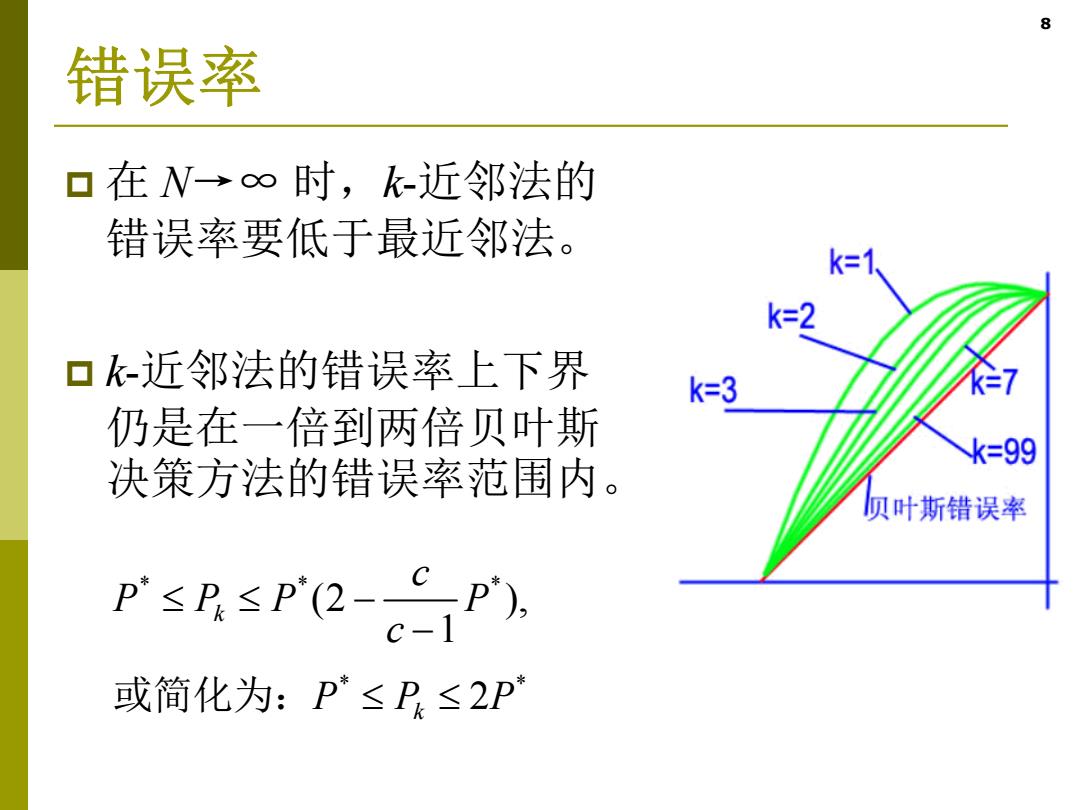
8 错误率 口在N→∞时,k-近邻法的 错误率要低于最近邻法。 k=1 k=2 口k-近邻法的错误率上下界 k=3 7 仍是在一倍到两倍贝叶斯 k=99 决策方法的错误率范围内。 贝叶斯错误率 P≤月≤P2-cP 或简化为:P*≤P≤2P
8 错误率 在 N→∞ 时,k-近邻法的 错误率要低于最近邻法。 k-近邻法的错误率上下界 仍是在一倍到两倍贝叶斯 决策方法的错误率范围内。 ** * * * (2 ), 1 2 k k c P PP P c PP P 或简化为:

改进的近邻法
改进的近邻法

10 快速搜索近邻法 口基本思想:将样本集按邻近关系分组,求出每组 的质心,以及组内样本到该质心的最大距离;这 些组又可形成层次结构,即将组又分子组;因而 待识别样本可将搜索近邻的范围从某一大组,逐 渐深入到其中的子组,直至树的叶结点所代表的 组,确定其相邻关系。 口算法过程 ■训练样本集的分级分解; ■搜索
10 快速搜索近邻法 基本思想:将样本集按邻近关系分组,求出每组 的质心,以及组内样本到该质心的最大距离;这 些组又可形成层次结构,即将组又分子组;因而 待识别样本可将搜索近邻的范围从某一大组,逐 渐深入到其中的子组,直至树的叶结点所代表的 组,确定其相邻关系。 算法过程 训练样本集的分级分解; 搜索