
第八章 非监督学习方法 2010.12.20
第八章 非监督学习方法 2010.12.20

2 近邻函数准则算法 近邻函数:如y:是y的第I个近邻,则y:对y 的近邻系数为I;如y是y:的第K个近邻,则y 对y的近邻系数为K;y,和y;之间的近邻函数: a=I+K-2,i≠;&m=2N; 口连接:如y,和y,被分到同一类,则相互连接; 连接损失:两点之间的近邻函数a 如两点不 同类,则损失为0: NN 总类内损失:Lmn=∑∑a, i=1 i=l
2 近邻函数准则算法 近邻函数:如 yi是 yj的第 I 个近邻,则 yi对 yj 的近邻系数为 I;如 yj 是 yi 的第 K 个近邻,则 yj 对 yi 的近邻系数为 K;yi和 yj之间的近邻函数: 连接:如 yi 和 yj 被分到同一类,则相互连接; 连接损失:两点之间的近邻函数αij ;如两点不 同类,则损失为 0; 2, ; 2 ; ij ii I K i j N 1 1 . N N within ij i j L 总类内损失:
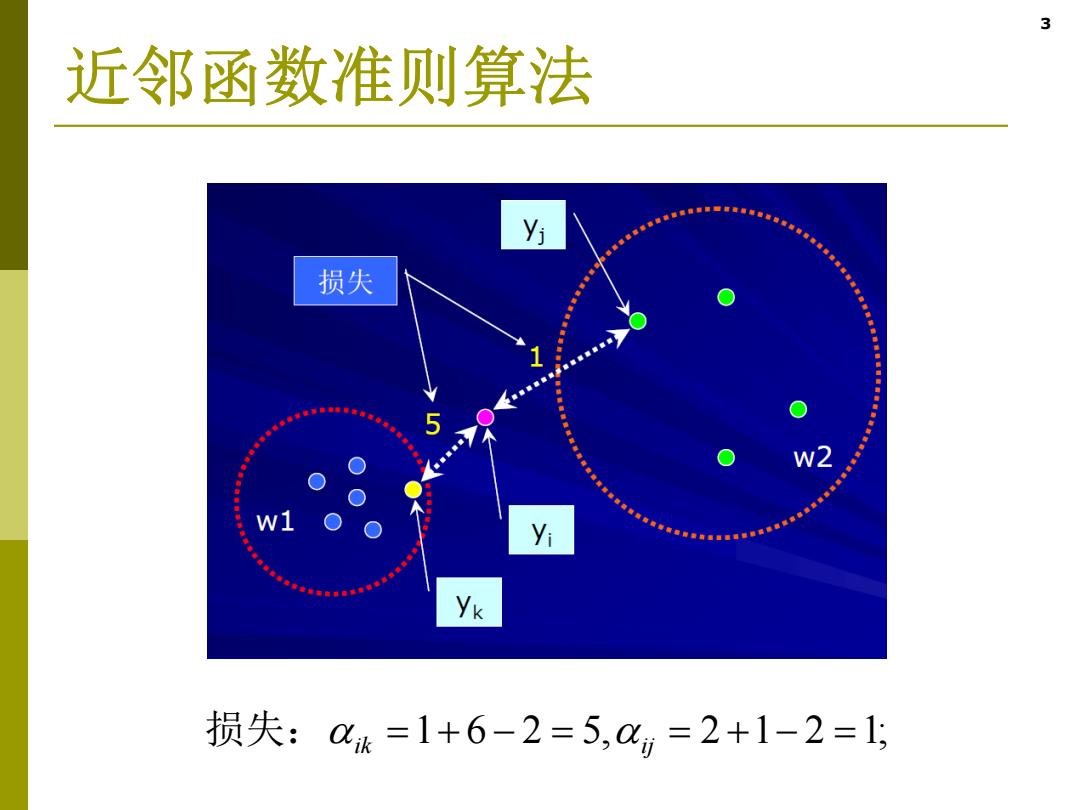
3 近邻函数准则算法 y为 损失 `w"W w2 w1 Vi yk 损失:0k=1+6-2=5,0x=2+1-2=1
3 近邻函数准则算法 损失: ik ij ;1212,5261

4 近邻函数准则算法 两类间的最小近邻函数:方m (a)月 口w与其余各类的最小近邻函数:=in': j≠1 ▣类间损失 -[(y:-aims)-(:-agmas)if 总类间损失: Yi>akimax if Y,≤1max,Y>Ck ma Yi+akmax ifY,>C1max,Y,≤k max =∑A; Yi+aimax +ak max ifY≤amax,Y1≤0 max i=1 其中Cmax、Ckmax是同一类中样本间的最大连接损失
4 近邻函数准则算法 两类间的最小近邻函数: ωi 与其余各类的最小近邻函数: 类间损失 , min ; k il j ij ij y y 1, , min ; i ij j c j i =1 ; c between i i L 总类间损失:

5 近邻函数准则算法 口算法步骤 1.计算距离矩阵△,其元素△=△(yy,)月 2.用距离矩阵计算近邻矩阵M,M表示y:是y的 第几个近邻; 3计算近邻函数矩阵L,L,M,+M-2L,L2N: 4.搜索L,连接每个点与其最近邻形成初始划分; 5.对每两个类计算Y和imax? jmax' 只要Y,小 于imax' a: imax 中的任何一个,就合并两类(建 立连接)。重复至没有新的连接为止
5 近邻函数准则算法 算法步骤 1. 计算距离矩阵 ∆,其元素 2. 用距离矩阵计算近邻矩阵 M , Mij 表示 yi 是 yj 的 第几个近邻; 3. 计算近邻函数矩阵 L , Lij = Mij + Mji –2 I , Lii =2 N; 4. 搜索 L,连接每个点与其最近邻形成初始划分; 5. 对每两个类计算γij 和αimax,αjmax,只要γij 小 于αimax,αjmax中的任何一个,就合并两类(建 立连接)。重复至没有新的连接为止。 );,( ij yy ji

分级聚类方法
分级聚类方法

7 两种策略 y2 Ya y1 yo ys ya 1-水平- 100 2-水平- 3-水平- 90 4-水平- 80 5-水平- 70 性 y1,y2,y3,y4y5 6-水平 y1,y2,y3 y4,y5 y1,y2 ys y
7 两种策略

8 类间相似性度量 口最近距离(single--link): A(T,「y)=min8(x,y), yerj 口最远距离(complete--link): A(rir)=max6(x,y), yerj 口均值距离(average-link): △(T,Tj)=6(m,mj)
8 类间相似性度量 最近距离(single-link): 最远距离(complete-link): 均值距离(average-link): ( , ) min ( , ), i j i j x y x y ( , ) max ( , ), i j i j x y x y ( , ) ( , ). ij i j m m

9 类间相似性度量对结果的影响 Single-Link Single-Link Method ab C d Euclidean Distance (1) (2) (3) b d b d d d a 2 6 5 6 a,bi 3) a,b,c 4 3 b 4 c 4 c Distance Matrix Complete-Link Method Complete-Link Euclidean Distance ab ca (1) (2) (3) b d b d C d c.d 3 5 654 a 53 65 a,b 56 a,b6 4 4 c y Distance Matrix
9 类间相似性度量对结果的影响

10 类间相似性度量对结果的影响 0 0 0 0 0 0 00 0 (a) 。0 0 0 00 0 0 0 0 0 00 0 0 (b) (6) 0 0 0 000 0 (c) (c) (c) 三种数据分布的例子 采用最近距离作为相似性度量 采用最远距离作为相似性度量
10 类间相似性度量对结果的影响