
第五章 非线性判别函数 2010-11-10
第五章 非线性判别函数 2010-11-10

分段线性判别函数
分段线性判别函数
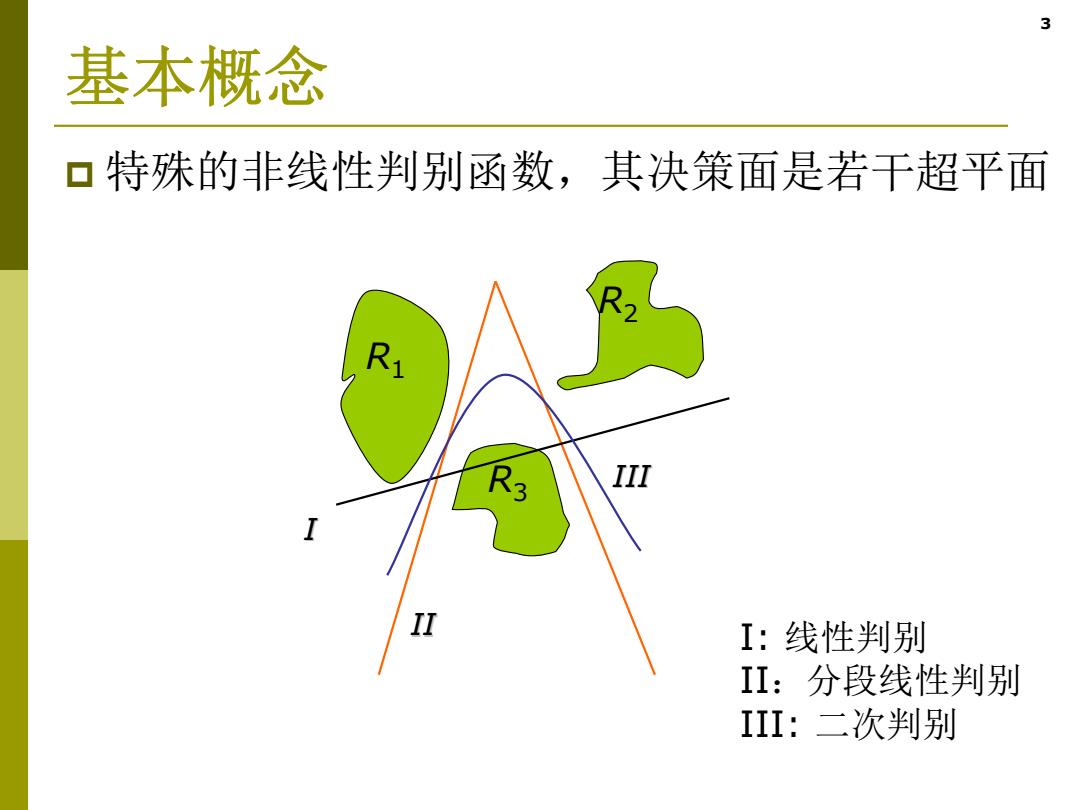
3 基本概念 口特殊的非线性判别函数,其决策面是若干超平面 I:线性判别 II:分段线性判别 III:二次判别
3 基本概念 特殊的非线性判别函数,其决策面是若干超平面 I: 线性判别 II:分段线性判别 III: 二次判别 R1 R3 R2 II I III

4 形式定义 口每个类由若干个子类组成,即0,={,,0} 口子类的线性判别函数: g(x)=wx+0,1=1,,l,i=1,,c 口o,类的判别函数:g,(x)=maxg(x), 1=1,2,,1 口决策规则: 8,()=max8,(x),则x∈0, i=1.2 口决策面方程: 8”(x)=8"(x)
4 形式定义 每个类由若干个子类组成,即 子类的线性判别函数: ωi 类的判别函数: 决策规则: 决策面方程: 0 ( ) , 1,..., , 1,..., ; T l ll i ii i g ll x wx i c 1,, ; il ii i 1,2,..., ( ) max ( ), i l i i l l g g x x 1,2,..., ( ) max ( ), ; j ij i c g g x xx 则 ( ) ( ). n m i j g g x x

基于距离的 分段线性判别函数
基于距离的 分段线性判别函数
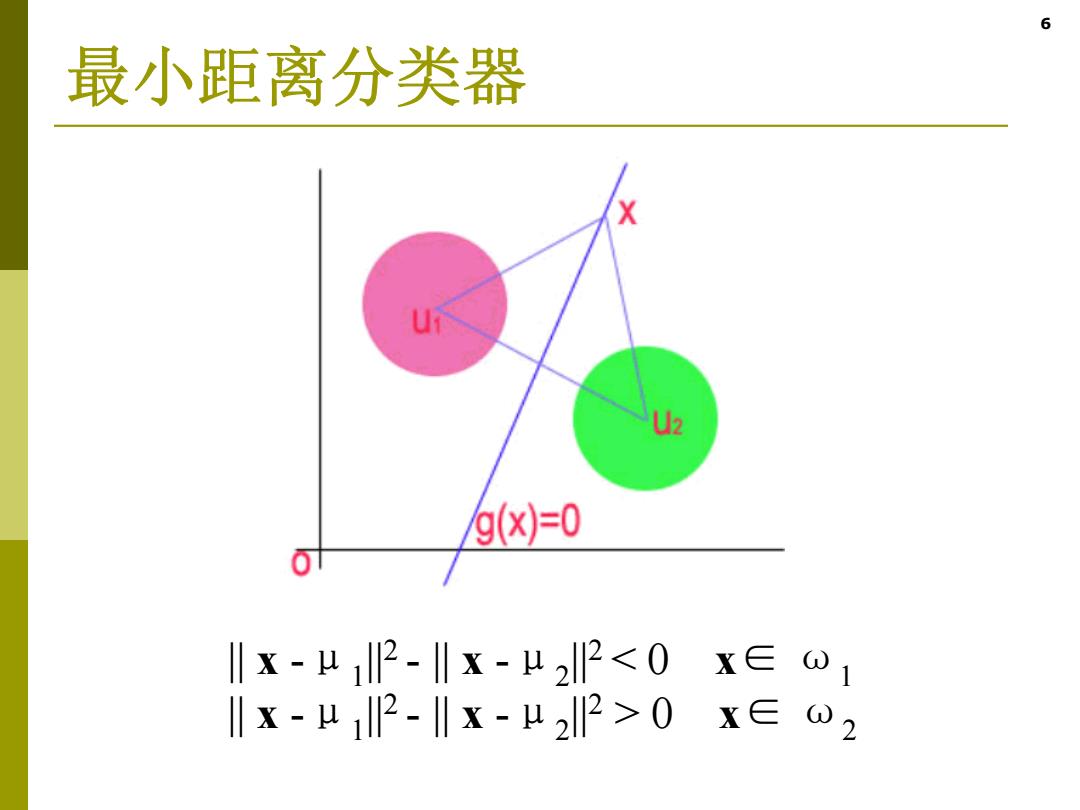
6 最小距离分类器 X 2 9(x)=0 x-μ2-‖x-μ220X∈w2
6 最小距离分类器 || x - μ1 ||2 - || x - μ2 ||2 0 x∈ ω 2
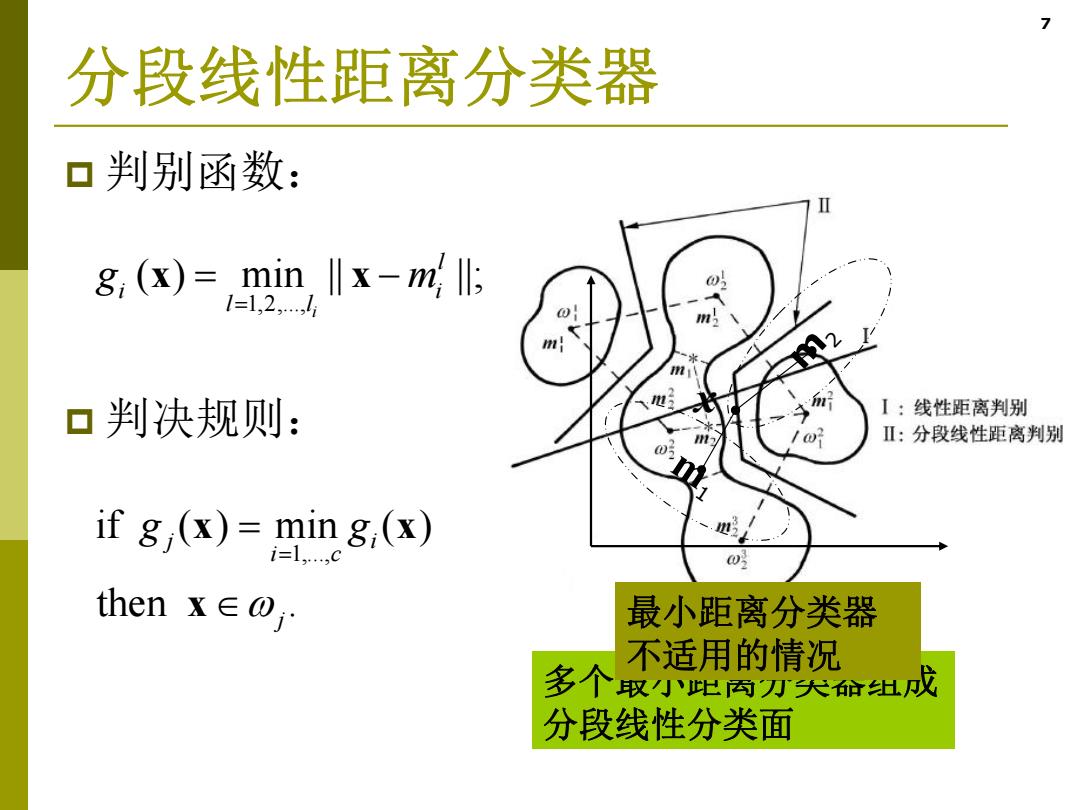
7 分段线性距离分类器 口判别函数: 8,()=mnX-m店 口判决规则: I:线性距离判别 Ⅱ:分段线性距离判别 if g (x)=ming.(x) then x∈0jr 最小距离分类器 不适用的情况 多个取小距肉引尖位丝成 分段线性分类面
7 分段线性距离分类器 判别函数: 判决规则: 1,2,..., ( ) min || ||; i l i i l l g m x x 1,..., if ( ) min ( ) then . j i i c j g g x x x 多个最小距离分类器组成 分段线性分类面 最小距离分类器 不适用的情况 m1 m2 x

错误修正算法
错误修正算法

9 简介 算法原理:ay是增广权向量a与规范化的增广 样本向量y的内积,其值描述两个向量在方向上 的一致性; 算法条件:已知每类的子类数日↓,但未知子 类划分的情况; 算法思路:先假设初始的权向量;后由训练样本 提供的错误信息进行迭代修正,直至收敛
9 简介 算法原理:aiTy 是增广权向量 ai 与规范化的增广 样本向量 y 的内积,其值描述两个向量在方向上 的一致性; 算法条件:已知每类的子类数目 li ,但未知子 类划分的情况; 算法思路:先假设初始的权向量;后由训练样本 提供的错误信息进行迭代修正,直至收敛

10 算法步骤 1. 初始化:任意给定各子类的权向量 a(0),i=1,2,…,C,1=1,2,…,l 2.检测: a"()'ymax'y, ifa(k)y,>a(k)y,i≠j,1=1,…, →y被正确分类,无需修正: 臼子类o"(i≠j)s.ta(k)'y,≤a(k)y →y,被错分,需修正;
10 算法步骤 1. 初始化:任意给定各子类的权向量 ail(0), i=1,2,…,c, l=1,2,…,li ; 2. 检测: )( ,)(max,,2,1 j Tlj ll j Tmj k k j ya ya if ( ) ( ) , , 1, , mT lT j j i j i j k ki j l l a ya y y 被正确分类,无需修正; ( ) . . ( ) ( ) n m T n T i j j i j j i j st k k a y a y y 子类 被错分,需修正;