
第八章 非监督学习方法 2010.12.13
第八章 非监督学习方法 2010.12.13

引言
引言
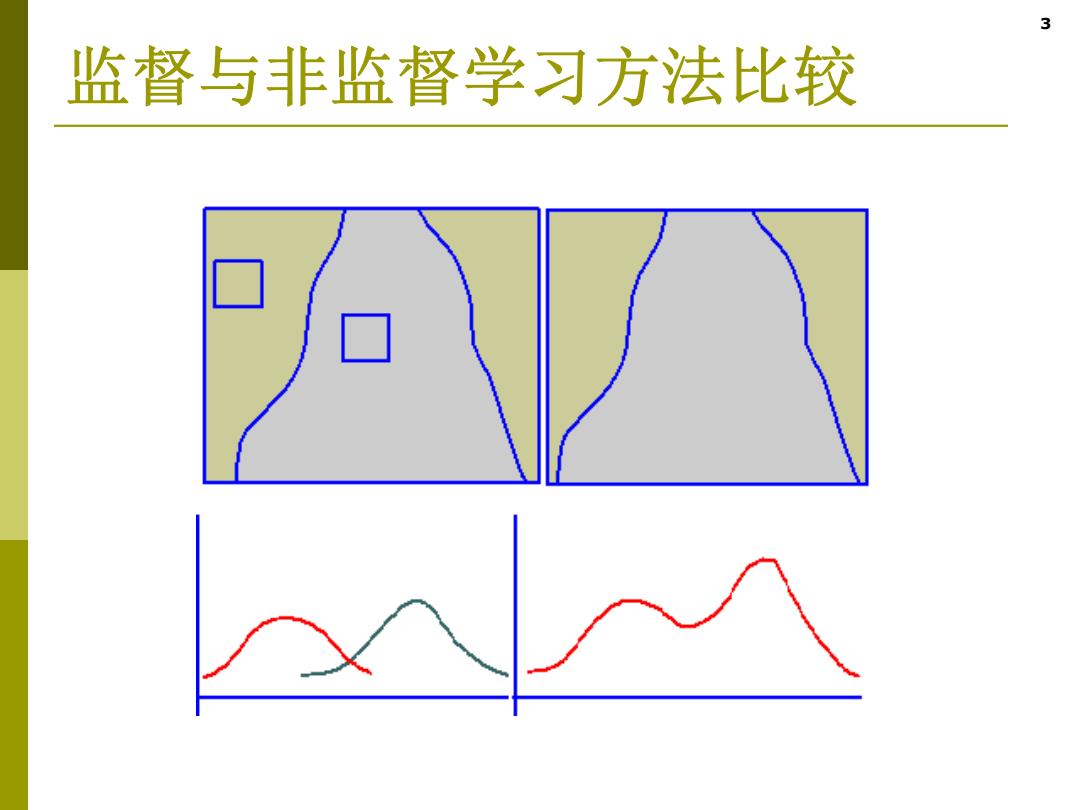
3 监督与非监督学习方法比较 口
3 监督与非监督学习方法比较

4 两大类非监督学习方法 1.基于概率密度函数估计的直接方法:设法找到 各类别在特征空间的分布参数再进行分类。比 如直方图方法。 2. 基于样本间相似性度量的间接聚类方法:设法 定出不同类别的核心或初始类核,然后依据样 本与各核心之间的相似性度量将样本聚集成不 同类别
4 两大类非监督学习方法 1. 基于概率密度函数估计的直接方法:设法找到 各类别在特征空间的分布参数再进行分类。比 如直方图方法。 2. 基于样本间相似性度量的间接聚类方法:设法 定出不同类别的核心或初始类核,然后依据样 本与各核心之间的相似性度量将样本聚集成不 同类别
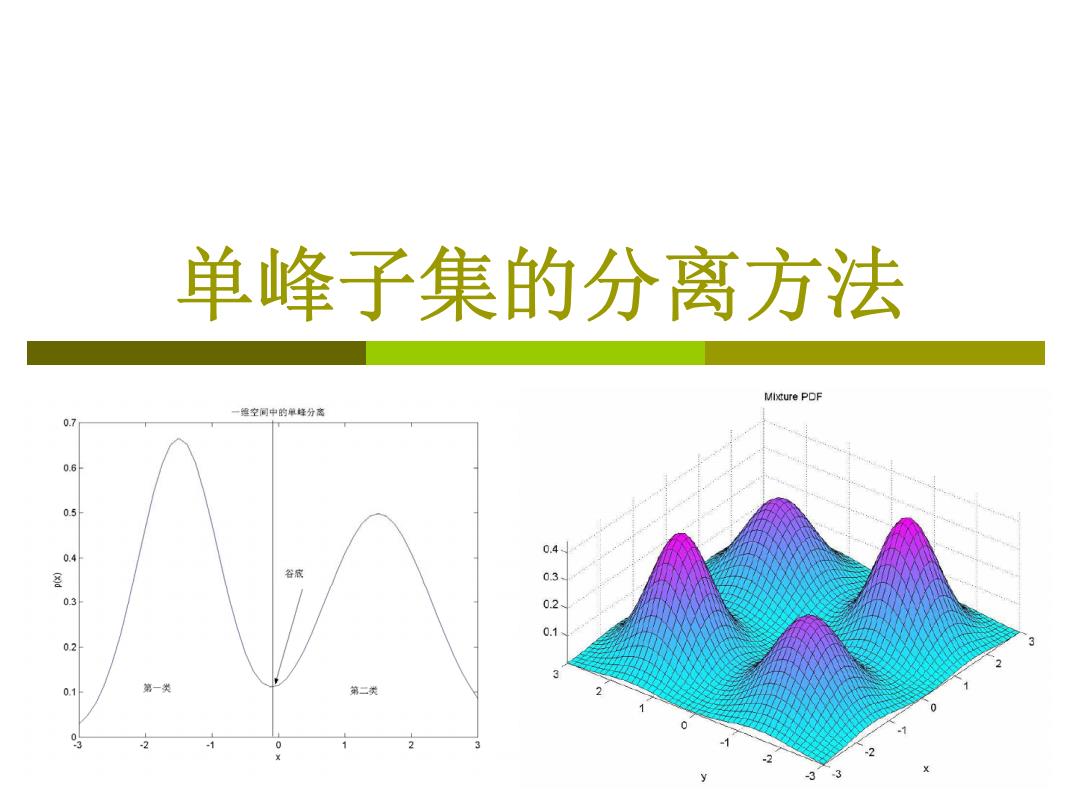
单峰子集的分离方法 Mixture PDF 一维空同中的佩峰分离 0.7 0.6 05 0.4 0.4 容成 0.3 0.3 0.2 0.1 02 0.1 第一类 第二类 1 0 -2 3
单峰子集的分离方法
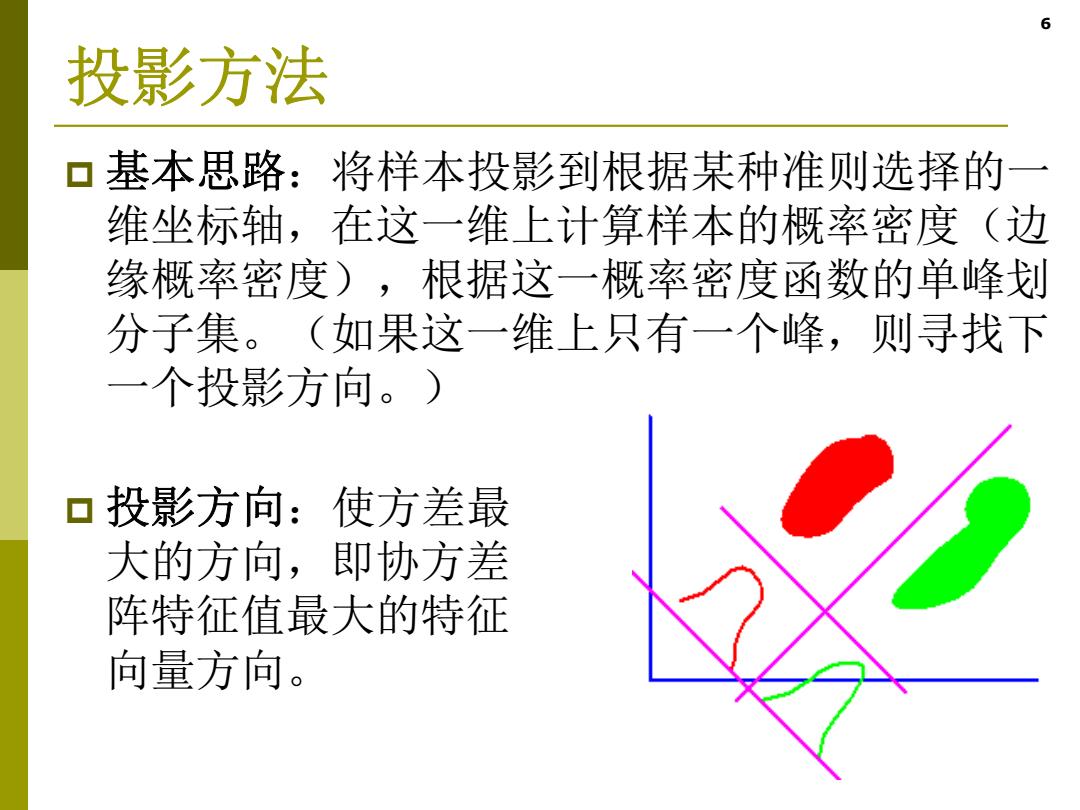
6 投影方法 基本思路:将样本投影到根据某种准则选择的一 维坐标轴,在这一维上计算样本的概率密度(边 缘概率密度),根据这一概率密度函数的单峰划 分子集。(如果这一维上只有一个峰,则寻找下 一个投影方向。) 口投影方向:使方差最 大的方向,即协方差 阵特征值最大的特征 向量方向
6 投影方法 基本思路:将样本投影到根据某种准则选择的一 维坐标轴,在这一维上计算样本的概率密度(边 缘概率密度),根据这一概率密度函数的单峰划 分子集。(如果这一维上只有一个峰,则寻找下 一个投影方向。) 投影方向:使方差最 大的方向,即协方差 阵特征值最大的特征 向量方向

7 投影方法 口算法步骤 1.计算样本的混合协方差矩阵的最大特征值对应的 特征向量u,将样本投影到u上(K-L变换); 2.对投影后的数据,估计概率密度函数; 3.找到边缘概率密度函数的各谷点,在这些谷点上 作垂直于Ⅱ的超平面得到子集的划分; 4.如果没有谷点,则用下一个最大的特征值代替, 重复步骤2~3; 5.对所得到的各个子集进行同样的过程,直至每个 子集都是单峰为止
7 投影方法 算法步骤 1. 计算样本的混合协方差矩阵的最大特征值对应的 特征向量 u,将样本投影到 u 上 (K-L变换); 2. 对投影后的数据,估计概率密度函数; 3. 找到边缘概率密度函数的各谷点,在这些谷点上 作垂直于 u 的超平面得到子集的划分; 4. 如果没有谷点,则用下一个最大的特征值代替, 重复步骤 2~3; 5. 对所得到的各个子集进行同样的过程,直至每个 子集都是单峰为止
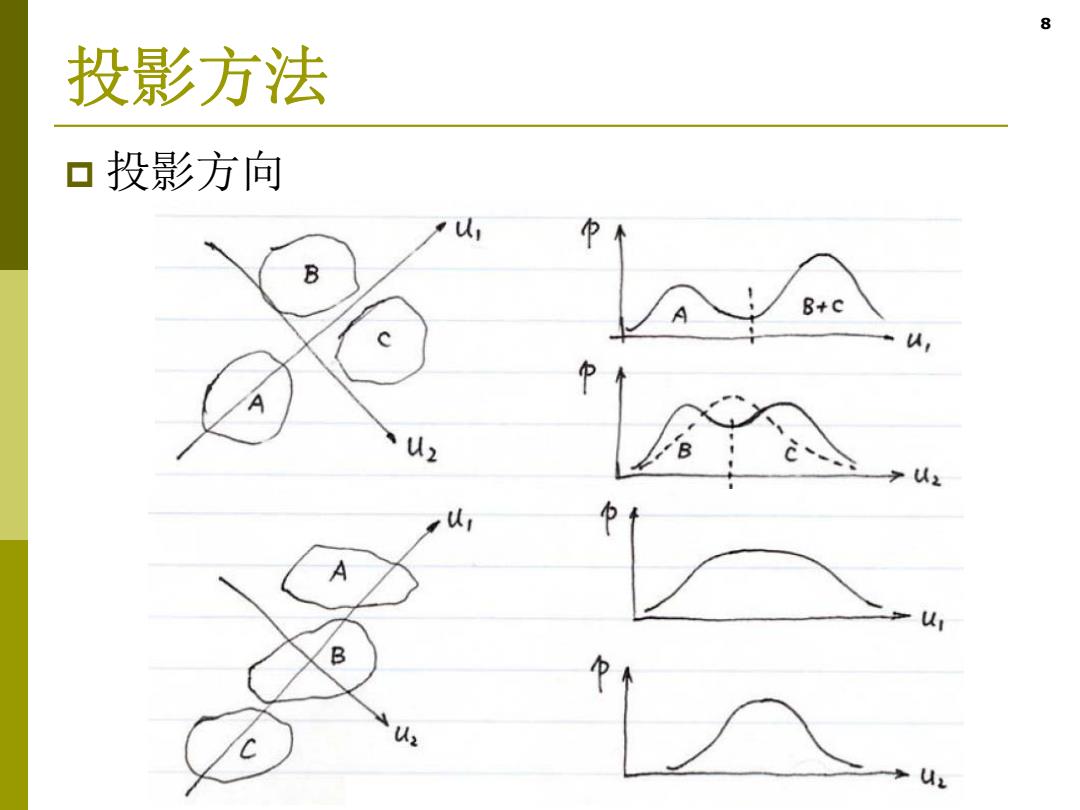
8 投影方法 口投影方向 B A B+c ur u2 , A B 42
8 投影方法 投影方向

9 单峰子集分离的迭代算法 口聚类准则函数 J=∫∑∑fw1r,)-fwIr,川, i=1 j=1 where S=Ur,,I ,∩r,=0(i=j), i=1 r=N,∑N,=N=lSg f() f(川2)
9 单峰子集分离的迭代算法 聚类准则函数 2 1 1 1 1 [ ( | ) ( | )] ( ) , 2 where , ( ), , ; c c i j i j c iij i ii i i J ff p d S ij N NNS y y yy

10 单峰子集分离的迭代算法 口迭代算法求解极值 ■ 考查某个样本yk从「;移入T: f(y|i)≥f(yIr;,f(yI,)≤f(y|r,) adA=-y,=K.y方 AJ =[[2eA,]p(y)dy +2cf(yIr,)-f(yr)fp(y)dy
10 单峰子集分离的迭代算法 迭代算法求解极值 考查某个样本 yk 从Γ j 移入Γ i: ( | ) ( | ), ( | ) ( | ), 1 and ( , ); i i j j ij k ff f f ffK N yy y y y y 2 2 () 2 ( | ) ( | ) () , i i ji J cf p d c fff p d y y y y yy