
2010/10/11 第三章 概率密度函数的估计 引言 2010-10-11 基于样本的两步Bayes决策 类的先验概率的估计 样本分布的 决策规则: 口依靠经验: 训练样本集 统计特征: 判别函致 概率密度函数 决策面方程 口用训练数据中各类出现的频率估计: 1.根据样本估计 Po,)和xo,): 口用频率估计概率的优点: 2.用估计的概率密度设计贝叶斯分类器。 ·无偏性: 希望:当样本数N一o时,得到的分类器收敛 于理论上的最优解。则需要 ■相合性: xo,)→p(xa,) ■收敛速度快。 Pa)v→Po,) 类条件概率密度的估计 概率密度函数的估计方法 口概率密度函数可是满足下面条件的任何函数: 样本所 总体概率密度推断 解决方法 p(x)≥0, ∫p(x)dk=l 属类别 函数的形式 监督参 己知 已知 参数 最大似然估计 口两种主要的估计思路: 数估计 贝叶斯估计 非监督 未知 已知 ■参数估计:概率密度函数的形式已知,而表征函 参数估 数的参数未知,通过训练数据来估计: ■非参数估计:密度函数的形式未知,也不作假设, 非参数 已知 未知 率 Parzen窗法 利用训练数据直接对概率密度进行估计。 估计 密度 近邻法 最 1
2010/10/11 1 第三章 概率密度函数的估计 2010-10-11 引言 3 1. 根据样本估计 和 ; 2. 用估计的概率密度设计贝叶斯分类器。 希望:当样本数N→∞时,得到的分类器收敛 于理论上的最优解。则需要 基于样本的两步Bayes决策 ( ) ˆ P i ˆ(| )i p x 训练样本集 样本分布的 统计特征: 概率密度函数 决策规则: 判别函数 决策面方程 4 类的先验概率的估计 依靠经验; 用训练数据中各类出现的频率估计; 用频率估计概率的优点: 无偏性; 相合性; 收敛速度快。 5 类条件概率密度的估计 概率密度函数可是满足下面条件的任何函数: 两种主要的估计思路: 参数估计:概率密度函数的形式已知,而表征函 数的参数未知,通过训练数据来估计; 非参数估计:密度函数的形式未知,也不作假设, 利用训练数据直接对概率密度进行估计。 6 概率密度函数的估计方法 样本所 属类别 总体概率密度 函数的形式 推断 解决方法 监督参 数估计 已知 已知 参数 最大似然估计, 贝叶斯估计 非监督 参数估 计 未知 已知 非参数 估计 已知 未知 概率 密度 函数 Parzen窗法、 kN近邻法

2010/10/11 参数估计的基本概念 估计量的评价 口统计量:样本集的某种函数 口无偏性(数学期望):E(⊙)=0 ),K={x,x2,,xw: 口参数空间:总体分布的未知参数日所有可能取 口有效性(风险小):va(⊙越小,越有效: 值组成的集合(⊙): 口点估计的估计量和估计值: ■日的估计量合=dx,x2,,xw)是样本集的函数: 口相合性(一致性):样本数趋于无穷时,日依概 率趋于0,即 。估计量对样本集的一次实现称为估计值。 po=-0. 假设条件 口参数日是确定而未知的量(非随机量): 最大似然估计 口样本集按类别分开,样本集K中样本都是从概 率密度为px)的总体中独立抽取出来(独立 同分布,ii.d.): 口概率密度函数的形式已知,参数未知,用 paw)表示,对于同类别可简化为px): 口K中的样本不包括日()中的信息,即不同 类别的参数在函数上是独立的。 似然函数 最大似然估计 口只考虑一类样本:独立地按概率密度px0抽 口目标:根据已抽取的N个样本x,2,,xw,估 取样本集K=x,x2,,Xw,用样本集K估计未 计这组样本“最可能”来自哪个密度函数: 知参数0: 口基本思路:如果在0=日下,《0最大,则日 口似然函数:在参数日下观测到样本集K的概率 应是“最可能”的参数值。 (联合分布)密度,是0的函数: 。是样本集的函数,记作6=d(x,2,,xw), 1O=PK18=p,sIo=直pKO 是日的最大似然估计量: 口对数化似然函数: =arg max()=arg max H0) H(0)-In/(0)-p(x.10) =gmn立n4|9 2
2010/10/11 2 7 参数估计的基本概念 统计量:样本集的某种函数 f(K),K={x1, x2 ,…, xN}; 参数空间:总体分布的未知参数 θ 所有可能取 值组成的集合(Θ); 点估计的估计量和估计值: Θ 的估计量 = d(x1, x2 ,…, xN) 是样本集的函数; 估计量对样本集的一次实现称为估计值。 ˆ 8 估计量的评价 无偏性(数学期望): 有效性(风险小): 越小,越有效; 相合性(一致性):样本数趋于无穷时, 依概 率趋于θ,即 ˆ E ; ˆ var ˆ n 0. n lim P 最大似然估计 10 假设条件 参数 θ 是确定而未知的量(非随机量); 样本集按类别分开,样本集 Kj 中样本都是从概 率密度为 p(x|ωj) 的总体中独立抽取出来(独立 同分布,i.i.d.); 概率密度函数的形式已知,参数未知,用 p(x|ωi,θ) 表示,对于同类别可简化为 p(x|θ); Kj 中的样本不包括 θj (j≠i)中的信息,即不同 类别的参数在函数上是独立的。 11 似然函数 只考虑一类样本:独立地按概率密度 p(x|θ) 抽 取样本集 K={x1, x2 ,…, xN},用样本集 K 估计未 知参数 θ; 似然函数:在参数 θ 下观测到样本集 K 的概率 (联合分布)密度,是 θ 的函数: 对数化似然函数: 1 2 1 ( ) ( | ) ( , ,..., | ) ( | ); N N k k lp p p K xx x x 1 ( ) ln ( ) ln ( | ). N k k Hl p x 12 目标:根据已抽取的 N 个样本 x1, x2 ,…, xN,估 计这组样本“最可能”来自哪个密度函数; 基本思路:如果在 下,l(θ) 最大,则 应是“最可能”的参数值。 是样本集的函数,记作 , 是θ 的最大似然估计量: 最大似然估计 ˆ ˆ ˆ 1 2 ˆ ( , ,..., ) N d xx x argmax ln ( | ). argmax ( ) argmax ( ) ˆ 1 N k k ML p l H x

2010/10/11 14 最大似然估计 参数求解 口图解 口必要条件:函数梯度(导数)为0 ■如0是标量,且(0连续可微,则最大似然估计量 即满足方程: 4 0=0或0=0, 12x0 do de 8x0 407 ■如未知参数有S个分量,即0=[0,,…,]了,则最 大似然估计量满足S个方程: 2 54 V.H(0)-V,Inp(x.I0)=0. 其中, 。= 表示梯度算子。 参数求解 参数求解 口当必要条件有多个解时,使得似然函数为最大的 口讨论 解才是最大似然估计值。 p武,2xy1,82)= 1 10)=pK10)= (0,-4)产: 口如不满足连续可微,则无一般性方法,需用其他 0 方法求解。 H(0)=-NInl(0-0). 口例:随机变量x服从均匀分布,参数0,,未知 OH=N-1 -=0 a002- 0<x<0 w1 aH p(x0)- 90 0 other 最大似然估计量为0=xmim,h=xmax. 单变量正态分布的最大似然估计 单变量正态分布的最大似然估计 口未知参数:0=[0,0,],8=4,02=o VH0)=∑7。Inp(x0)=0; k 口样本集:K={x,x2,,xw}: V.In p(x 0)= 口总体分布: 2g2@-8 1 1 p(x10)=- 店… peo0=-h2a-2a低-8 1 3
2010/10/11 3 13 最大似然估计 图解 14 参数求解 必要条件:函数梯度(导数)为 0 如θ是标量,且 l(θ) 连续可微,则最大似然估计量 即满足方程: 如未知参数有 S 个分量,即θ=[θ1,θ2,…,θS]T,则最 大似然估计量满足 S 个方程: ( ) H( ) 0 0. dl d d d 或 1 1 ( ) ln ( | ) 0; N k k S H px 其中, , , 表示梯度算子。 15 参数求解 当必要条件有多个解时,使得似然函数为最大的 解才是最大似然估计值。 如不满足连续可微,则无一般性方法,需用其他 方法求解。 例:随机变量x服从均匀分布,参数θ1,θ2未知 1 2 2 1 1 (|) 0 other x p x 16 参数求解 讨论 12 12 2 1 2 1 1 21 2 21 1 ( , ,... | , ) () ( | ) ; ( ) 0 ( ) ln ( ); 1 0; 1 0; N N px x x l p H Nl H N H N K 最大似然估计量为θ1=xmin, θ2=xmax。 17 单变量正态分布的最大似然估计 未知参数: 样本集:K={x1, x2 ,…, xN}; 总体分布: 18 单变量正态分布的最大似然估计 1 ( ) ln ( | ) 0; N k k H px
2010/10/11 单变量正态分布的最大似然估计 单变量正态分布的最大似然估计 解得 加成-2 口均值的最大似然估计量是无偏的 -很容小 口方差的最大似然估计量不是无偏的 口多元正态分布 2- 立容加 ■方差的无偏估计为样本方差 2-时 单变量正态分布的最大似然估计 Goodness-of-fit(拟合优度) 口可用Kolmogorov-Smirnov(K-S)拟合优度检验法 来度量样本观察值的分布和特定的理论分布间的 Gaussian, The 吻合程度。 data is generated,and the three red curves na5a时0g时 口K-S检查样本观察值的累积概率分布函数和特定 and (1.56).Averaged across the three data 的累积概率分布函数之间的最大绝对偏差。 sets,the mean is correct.but the variance 6 口对一个概率模型未知的样本集,可假设不同的理 论分布且估计参数,后用K-S拟合优度检验法 (c) 选择和样本观察值分布的吻合程度最好的分布。 最大似然估计图例 贝叶斯估计 (a)True pdf is N(10,4).Estimated pdt is b)Tpdfs05N(10,0.1o)+0.5N(11,a2 ed pel is N(10.5,0.5) (c)True pdt is Gamma(4,4).Estimated pdls (d)Cumulative distribution functions for the ex reN(15.8,621)and Gamma(40,3.9 ample in(c以. ×
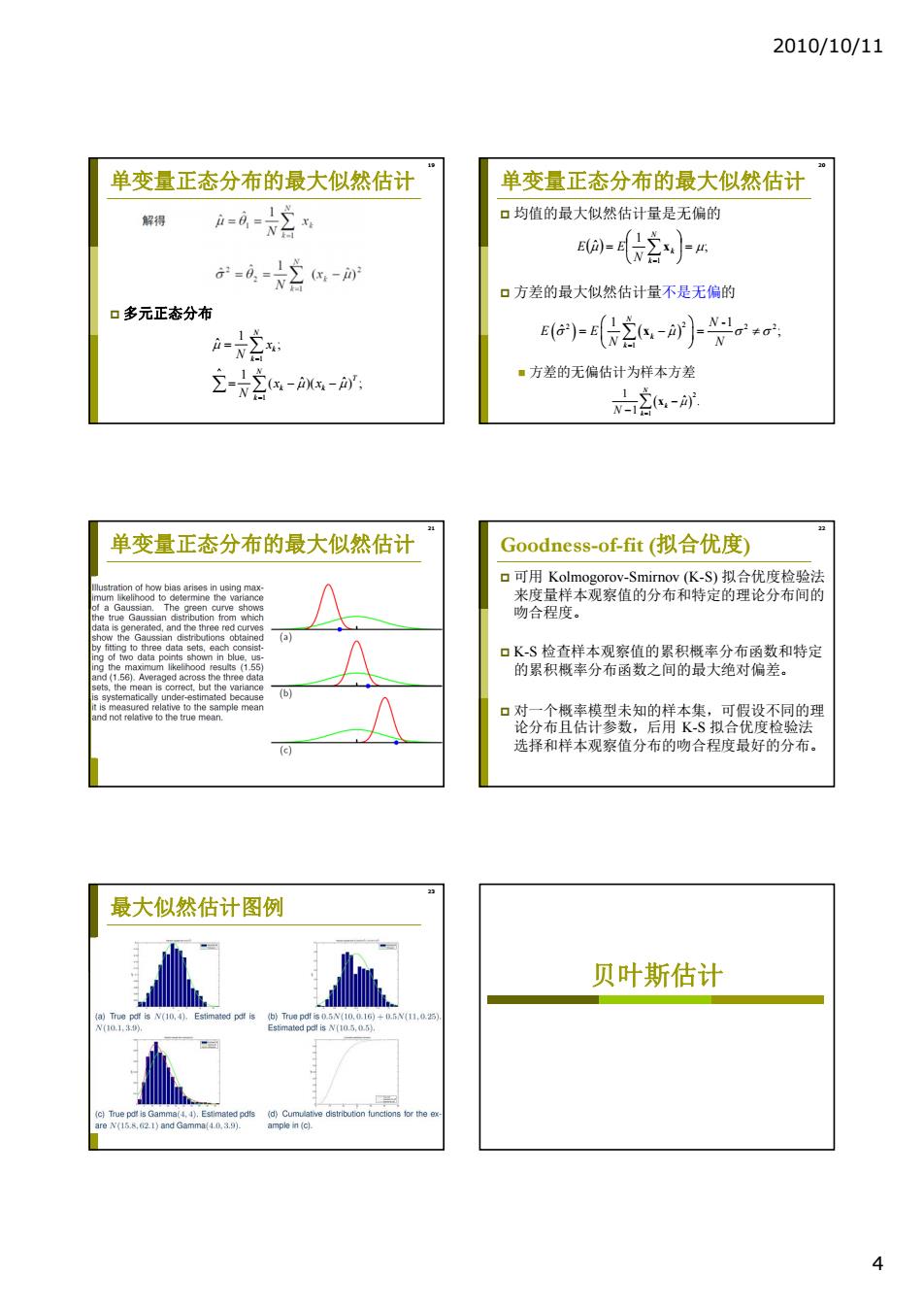
2010/10/11 4 19 单变量正态分布的最大似然估计 多元正态分布 1 ^ 1 1 ˆ ; 1 ( )( ) ; ˆ ˆ N k k N T k k k x N x x N 20 单变量正态分布的最大似然估计 均值的最大似然估计量是无偏的 方差的最大似然估计量不是无偏的 方差的无偏估计为样本方差 ; 1 ˆ 1 N k k N E E x 2 2 22 1 1 -1 ˆ ˆ ; N k k N E E N N x 2 1 1 ˆ . 1 N k N k x 单变量正态分布的最大似然估计 21 22 Goodness-of-fit (拟合优度) 可用 Kolmogorov-Smirnov (K-S) 拟合优度检验法 来度量样本观察值的分布和特定的理论分布间的 吻合程度。 K-S 检查样本观察值的累积概率分布函数和特定 的累积概率分布函数之间的最大绝对偏差。 对一个概率模型未知的样本集,可假设不同的理 论分布且估计参数,后用 K-S 拟合优度检验法 选择和样本观察值分布的吻合程度最好的分布。 23 最大似然估计图例 贝叶斯估计

2010/10/11 26 贝叶斯估计 最大后验概率估计 口思略:类似于贝叶斯决策,只是将离散的决策状 口基本思想:用样本集K={x,x2,,xw估计未知 态变成了连续的参数估计。 参数0:将待估计的参数看成随机变量,其先验 分布为p(:目标是使得后验概率p©K)最大。 决策问愿 估计问愿 样本x 样本集K rm p(1K)arg m )p() p(K) 决策a 估计量8 真实状态山 真实参数0 -arg mgx p(10)p(0)=arg max(1)+In p() 状态空间A是离散空间 参数空间日是连续空间 先验概率P(w) 参数的先验分布p0 最大后验概率估计 口和最大似然估计的关系 ■当样本数趋于无穷时,最大后验概率估计一般趋 向于最大似然估计。 ■最大似然估计也可看作参数的先验概率密度函数 服从均匀分布(相当于没有先验知识)的最大后 验概率估计。 ■当参数的先验概率密度函数比较准确时,最大后 验概率估计的小样本性质大大优于最大似然估计。 5
2010/10/11 5 25 贝叶斯估计 思路:类似于贝叶斯决策,只是将离散的决策状 态变成了连续的参数估计。 决策问题 估计问题 样本 x 决策αi 真实状态ωi 状态空间A是离散空间 先验概率 P(ωi) 样本集 K 估计量 真实参数θ 参数空间Θ 是连续空间 参数的先验分布 p(θ) ˆ 26 最大后验概率估计 基本思想:用样本集 K={x1, x2 ,…, xN} 估计未知 参数θ;将待估计的参数θ看成随机变量,其先验 分布为p(θ);目标是使得后验概率 p(θ| K) 最大。 MAP 1 ( | )() ˆ arg max ( | ) arg max ( ) arg max ( | ) ( ) arg max ln ( | ) ln ( ); N k k p p p p pp p p x K K K K ln ( | ) ln ( ) 0. 1 N k k p x p 27 最大后验概率估计 和最大似然估计的关系 当样本数趋于无穷时,最大后验概率估计一般趋 向于最大似然估计。 最大似然估计也可看作参数的先验概率密度函数 服从均匀分布(相当于没有先验知识)的最大后 验概率估计。 当参数的先验概率密度函数比较准确时,最大后 验概率估计的小样本性质大大优于最大似然估计