
命议六学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 第二节集合的基本运算 在这一节中,我们主要介绍集合的并、交、差三种 基本运算,这三种运算的基本规律,以及它们与集合的 包含关系之间的基本关联 求实务实 踏实扎实
第二节 集合的基本运算 在这一节中,我们主要介绍集合的并、交、差三种 基本运算,这三种运算的基本规律,以及它们与集合的 包含关系之间的基本关联

P议衣学 情品课程 LIAOCHENG UNIVERSITY 定义121设A与B是两个集合。集合{xx∈域者x∈B} 称为集 厚德博学笃志精算 合A与集合B的并集或并,记作AUB,读为A并B。集合 {xx∈A饼且x∈B}称为集合A与集合B的交集或交,记作A∩B,读 为A交B。 若A∩B=☑,则称集合A与集合B无交或不相交;反之,若 A∩B≠☑,则称集合A与集合B有(非空的)交。集合{xx∈A并且x生B} 则称集合A与集合B的差集,记作A\B或A-B,读为A差B,或A减B。 求实务实 踏实扎实
定义 1.2.1 设 A 与 B 是两个集合。集合x x A x B 或者 称为集 合 A 与 集 合 B 的 并 集 或 并 , 记 作 A B ,读为 A 并 B 。 集 合 x x A x B 并且 称为集合 A 与集合 B 的交集或交,记作 A B , 读 为 A 交 B 。 若 A B = ,则称集合 A 与集合 B 无交或不相交;反之,若 A B ,则称集合 A 与集合 B 有(非空的)交。集合x x A x B 并且 则称集合 A 与集合 B 的差集,记作 A B\ 或 A B− ,读为 A 差 B ,或 A 减 B
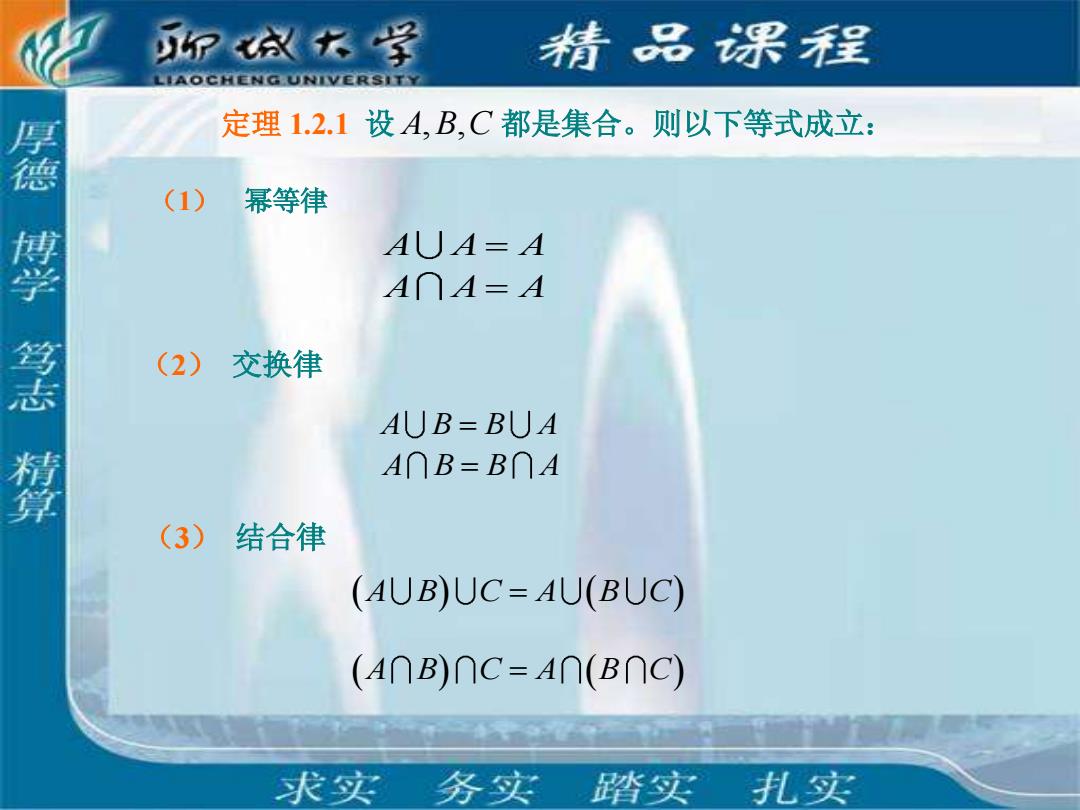
P放学 精品课程 LIAOCHENG UNIVERSITY 定理1.2.1设A,B,C都是集合。则以下等式成立: 厚德博学笃志精算 (1) 幂等律 AUA-A A∩A=A (2) 交换律 AUB=BUA A∩B=B∩A (3)结合律 (AUB)UC=AU(BUC) (A∩B)∩C=A∩(B∩C) 求实务实 踏实 扎实
( A B C A B C ) = ( ) ( A B C A B C ) = ( ) (1) 幂等律 A A A = A A A = 定理 1.2.1 设 A B C , , 都是集合。则以下等式成立: (2) 交换律 A B B A = A B B A = (3) 结合律

印放衣学精品课程 LIAOCHENG UNIVERSITY 厚德博学驾志精算 (④)分配律 (A∩B)UC=(AUC)∩(BUC) (AUB)∩C=(A∩C)U(B∩C) (5) De Morgan律 A-(BUC)=(A-B)∩(A-C) A-(B∩C)=(A-B)U(A-C) 求实务实 踏实扎实
(5) De Morgan 律 (4) 分配律 ( A B C A C B C ) = ( ) ( ) ( A B C A C B C ) = ( ) ( ) A B C A B A C − = − − ( ) ( ) ( ) A B C A B A C − = − − ( ) ( ) ( )

P放衣学 精品课程 LIAOCHENG UNIVERSITY 定理1.2.2设A,B是两个集合。下列三个条件等价: 厚德博学笃志精算 (1)ACB; (2) A∩B=A: (3) AUB=B。 定义1.2.2设X是一个基础集。对于X的任何一个子集A,我们称 X-A为A的补集或余集,并且记作CA,为了方便起见有时也记作A'。 定理1.2.3 设X是一个基础集。若AB为X的子集,则 AU☑=A; A∩☑=Q AUX=X; A∩X=6 AUA'=Y; A∩A=☑ (AUB)=A∩B; (A∩B=U A”=A 求实务实 踏实扎实
定理 1.2.3 设 X 是一个基础集。若 A B, 为 X 的子集,则 A A = ; A = A X X = ; A X A = A A X = ; A A = ( A B A B ) = ; ( A B A B ) = A A = 定理 1.2.2 设 A B, 是两个集合。下列三个条件等价: (1) A B ; (2) A B A = ; (3) A B B = 。 定义 1.2.2 设 X 是一个基础集。对于 X 的任何一个子集 A ,我们称 X A − 为 A 的补集或余集,并且记作CA,为了方便起见有时也记作 A

P放衣学 情品课程 LIAOCHENG UNIVERSITY 厚德博学驾志 小结 本节主要介绍了集合的并、交、差三种基本运算,验证了其基本运 算规律及它们与集合的包含关系之间的基本关联 有时我们会用到“有限个集合的并(或交)”这样一个说法,这样说 精算 时总是指“某个集合的并(或交)”这里注意,我们迄今并未定义过 C 0 个集合的并(或交),尽管我们将来还会以某种方式定义“0个集合的 并”,但我们永远不用“0个集合的交”这种说法 求实务实 踏实扎实
小结 n + n + n + nx x A x B + 并且 本节主要介绍了集合的并、交、差三种基本运算,验证了其基本运 算规律及它们与集合的包含关系之间的基本关联. 有时我们会用到“有限个集合的并(或交)”这样一个说法,这样说 时总是指“某个集合的并(或交)”.这里注意,我们迄今并未定义过 0 个 集 合 的 并 ( 或 交 ), 尽 管 我 们 将 来 还 会 以 某 种 方 式 定 义“0 个集合的 并”,但我们永远不用“0 个集合的交”这种说法