
§4.4局部连通空间
§4.4局部连通空间
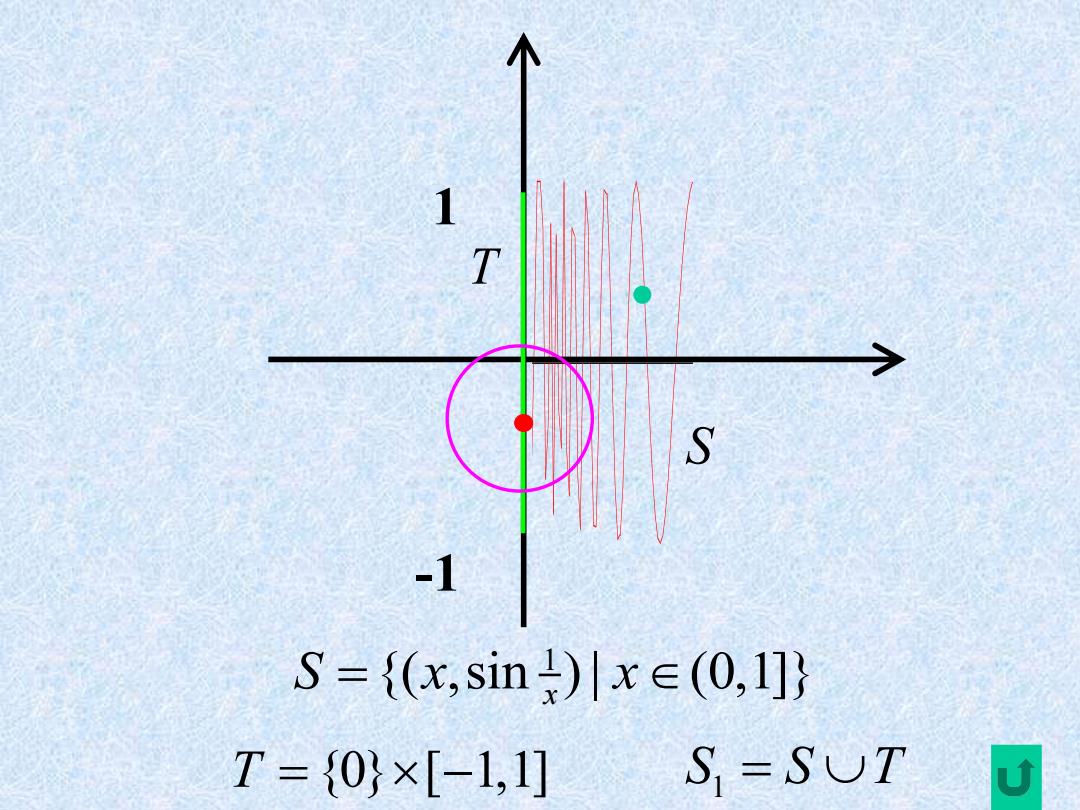
1 T S -1 S={(x,sin)川x∈(0,l]} T=0}×[-1,1] S=SUT U
0 0.5 1 2 2 sin 1 x B xA -1 1 1 {( ,sin ) | (0,1]} x S x x = T = − {0} [ 1,1] 1 S S T = S T

定义4.1.1设X是一个拓扑空 间,x∈X.如果x的每一个邻域U中 都包含着x的某一个连通邻域V, 则称拓扑空间X在点x处是局部连 通的. 如果拓扑空间X在它的每一个 点处都是局部连通的,则称X是一 个局部连通空间
定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间. 定义4.1.1 设 X 是一个拓扑空 间,x∈X. 如果 x 的每一个邻域 U 中 都包含着 x 的某一个连通邻域 V , 则称拓扑空间 X 在点 x 处是局部连 通的. 如果拓扑空间 X 在它的每一个 点处都是局部连通的,则称 X 是一 个局部连通空间

注 意 连通性和局部连通性没有必然 的蕴含关系 在刚才的例子中S,是连通空间,但 不是局部连通空间. 见图 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间
注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S 见图 注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S 注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S 注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S 注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S 注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S 注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S 注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S 注 意 连通性和局部连通性没有必然 的蕴含关系. 在刚才的例子中 是连通空间,但 不是局部连通空间. 每一个离散空间都是局部连通空 间,而多于两个点的离散空间都不 是连通空间. 1 S

拓扑空间X在点x∈X处是局部连 通的充要条件是x的所有连通邻域 构成点x处的一个邻域基
拓扑空间 X 在点 x∈ X 处是局部连 通的充要条件是 x 的所有连通邻域 构成点 x 处的一个邻域基. 拓扑空间 X 在点 x∈ X 处是局部连 通的充要条件是 x 的所有连通邻域 构成点 x 处的一个邻域基. 拓扑空间 X 在点 x∈ X 处是局部连 通的充要条件是 x 的所有连通邻域 构成点 x 处的一个邻域基

定理4.4.1设X是一个拓扑空 间.则下列条件等价: ()X是一个局部连通空间; (2)X的任何一个开集的任何一个 连通分支都是开集; (3)X有一个基,它的每一个元素 都是连通的
定理4.4.1 设 X 是一个拓扑空 间. 则下列条件等价: (1) X 是一个局部连通空间; (2) X 的任何一个开集的任何一个 连通分支都是开集; (3) X 有一个基,它的每一个元素 都是连通的. 定理4.4.1 设 X 是一个拓扑空 间. 则下列条件等价: (1) X 是一个局部连通空间; (2) X 的任何一个开集的任何一个 连通分支都是开集; (3) X 有一个基,它的每一个元素 都是连通的. 定理4.4.1 设 X 是一个拓扑空 间. 则下列条件等价: (1) X 是一个局部连通空间; (2) X 的任何一个开集的任何一个 连通分支都是开集; (3) X 有一个基,它的每一个元素 都是连通的. 定理4.4.1 设 X 是一个拓扑空 间. 则下列条件等价: (1) X 是一个局部连通空间; (2) X 的任何一个开集的任何一个 连通分支都是开集; (3) X 有一个基,它的每一个元素 都是连通的. 定理4.4.1 设 X 是一个拓扑空 间. 则下列条件等价: (1) X 是一个局部连通空间; (2) X 的任何一个开集的任何一个 连通分支都是开集; (3) X 有一个基,它的每一个元素 都是连通的. 定理4.4.1 设 X 是一个拓扑空 间. 则下列条件等价: (1) X 是一个局部连通空间; (2) X 的任何一个开集的任何一个 连通分支都是开集; (3) X 有一个基,它的每一个元素 都是连通的. 定理4.4.1 设 X 是一个拓扑空 间. 则下列条件等价: (1) X 是一个局部连通空间; (2) X 的任何一个开集的任何一个 连通分支都是开集; (3) X 有一个基,它的每一个元素 都是连通的

证明:()→(2)设C是X的一个开集 U的一个连通分支.若x∈C,则U 是x的一个邻域,由于X是一个局部 连通空间,从而x有一个连通邻域V 包含于U,因为V⌒C不是空集, 所以VcC,因此C是x的邻域, 故C是开集
证明: 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C 证明: (1) (2) 设 C 是 X 的一个开集 U 的一个连通分支. 若 x∈C ,则 U 是 x 的一个邻域,由于X 是一个局部 连通空间,从而 x 有一个连通邻域 V 包含于U ,因为 不是空集, 所以 ,因此 C 是 x 的邻域, 故 C 是开集. V C V C (1) (2)

(2)→(3)若(2)成立,则X的所 有开集的所有连通分支构成的集族 B恰是X的一个基. (3)→(1)显然. 注:在局部连通空间中,连通分支 即开又闭
若(2)成立,则X 的所 有开集的所有连通分支构成的集族 B 恰是X 的一个基. 显然. 注: 在局部连通空间中,连通分支 即开又闭. (2) (3) (3) (1) 若(2)成立,则X 的所 有开集的所有连通分支构成的集族 B 恰是X 的一个基. 显然. 注: 在局部连通空间中,连通分支 即开又闭. (2) (3) (3) (1) 若(2)成立,则X 的所 有开集的所有连通分支构成的集族 B 恰是X 的一个基. 显然. 注: 在局部连通空间中,连通分支 即开又闭. (2) (3) (3) (1) 若(2)成立,则X 的所 有开集的所有连通分支构成的集族 B 恰是X 的一个基. 显然. 注: 在局部连通空间中,连通分支 即开又闭. (2) (3) (3) (1) 若(2)成立,则X 的所 有开集的所有连通分支构成的集族 B 恰是X 的一个基. 显然. 注: 在局部连通空间中,连通分支 即开又闭. (2) (3) (3) (1) 若(2)成立,则X 的所 有开集的所有连通分支构成的集族 B 恰是X 的一个基. 显然. 注: 在局部连通空间中,连通分支 即开又闭. (2) (3) (3) (1) 若(2)成立,则X 的所 有开集的所有连通分支构成的集族 B 恰是X 的一个基. 显然. 注: 在局部连通空间中,连通分支 即开又闭. (2) (3) (3) (1)

定理4.4.2设X和Y都是拓扑 空间,其中X是局部连通空间, f:X>Y是一个连续开映射. 则∫()是一个局部连通空间. 证明:由于X是局部连通空间, 由th4,.2.1知X有一个基B,其中的 每一个成员都是连通的
定理4.4.2 设 X 和 Y 都是拓扑 空 间, 其 中 X 是局部连通空间, 是 一 个 连 续 开 映 射 . 则 f (X)是一个局部连通空间. 证明: 由于X 是局部连通空间, 由th4,.2.1知X 有一个基B ,其中的 每一个成员都是连通的. f X Y : → 定理4.4.2 设 X 和 Y 都是拓扑 空间, 其中 X 是局部连通空间, 是 一 个 连 续 开 映 射 . 则 f (X)是一个局部连通空间. 证明: 由于X 是局部连通空间, 由th4,.2.1知X 有一个基B ,其中的 每一个成员都是连通的. f X Y : → 定理4.4.2 设 X 和 Y 都是拓扑 空 间, 其 中 X 是局部连通空间, 是 一 个 连 续 开 映 射 . 则 f (X)是一个局部连通空间. 证明: 由于X 是局部连通空间, 由th4,.2.1知X 有一个基B ,其中的 每一个成员都是连通的. f X Y : → 定理4.4.2 设 X 和 Y 都是拓扑 空 间, 其 中 X 是局部连通空间, 是 一 个 连 续 开 映 射 . 则 f (X)是一个局部连通空间. 证明: 由于X 是局部连通空间, 由th4,.2.1知X 有一个基B ,其中的 每一个成员都是连通的. f X Y : → 定理4.4.2 设 X 和 Y 都是拓扑 空 间, 其 中 X 是局部连通空间, 是 一 个 连 续 开 映 射 . 则 f (X)是一个局部连通空间. 证明: 由于X 是局部连通空间, 由th4,.2.1知X 有一个基B ,其中的 每一个成员都是连通的. f X Y : → 定理4.4.2 设 X 和 Y 都是拓扑 空 间, 其 中 X 是局部连通空间, 是 一 个 连 续 开 映 射 . 则 f (X)是一个局部连通空间. 证明: 由于X 是局部连通空间, 由th4,.2.1知X 有一个基B ,其中的 每一个成员都是连通的. f X Y : → 定理4.4.2 设 X 和 Y 都是拓扑 空 间, 其 中 X 是局部连通空间, 是 一 个 连 续 开 映 射 . 则 f (X)是一个局部连通空间. 证明: 由于X 是局部连通空间, 由th4,.2.1知X 有一个基B ,其中的 每一个成员都是连通的. f X Y : → 定理4.4.2 设 X 和 Y 都是拓扑 空 间, 其 中 X 是局部连通空间, 是 一 个 连 续 开 映 射 . 则 f (X)是一个局部连通空间. 证明: 由于X 是局部连通空间, 由th4,.2.1知X 有一个基B ,其中的 每一个成员都是连通的. f X Y : →

由于f是一个连续的开映射,从而 易知B={f(B)川B∈B}是由fX) 的连通开集构成的集族。 下面我们证明B是f(仪)的一个基, 设U是fX)的任意开集,则f(U) 是X中的一个开集,从而存在 B1CB,使得(U)=UBBB
由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 f (U ) 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 由于 f 是一个连续的开映射,从而 易知 是由 f (X ) 的连通开集构成的集族. 下面我们证明 是 f (X ) 的一个基. 设U 是 f (X ) 的任意开集,则 是 X 中的一个开集,从而存在 ,使得 B B = { ( ) | } f B B B B B 1 1 1 ( ) B B f U B − = 1 f U( ) −