
聊城大学数学科学学院 点来拓扑学 山东省精品果程 2008
1 点 集 拓 扑 学 山东省精品课程 (XYZ) (XYZ) (XYZ) ➢聊城大学数学科学学院 2008

拓扑学导论 •拓扑学是几何学的分支,且是与欧氏几何 不同的几何学分支 。研究对象:一般的几何图形(拓扑空间) ·中心任务:研究几何图形的一类性质即所 谓的拓扑性质,但这类性质与我们在欧氏 几何中研究的长度、角度、面积等不同。 2
2 拓 扑 学 导 论 ●拓扑学是几何学的分支,且是与欧氏几何 不同的几何学分支 ●研究对象:一般的几何图形(拓扑空间) ●中心任务:研究几何图形的一类性质即所 谓的拓扑性质,但这类性质与我们在欧氏 几何中研究的长度、角度、面积等不同

平面欧氏几何的研究对象与内容 ●研究对象:直线和圆构成的图形 ●研究内容:长度、角度、面积、全等: 两图形全等即经过平移、旋转、对称两 图形重合;而长度、角度、面积经过上 述正交变换保持不变。 ●结论:欧氏几何研究图形在正交变换 下的不变性和不变量。 3
3 平面欧氏几何的研究对象与内容 ●研究对象:直线和圆构成的图形 ●研究内容:长度、角度、面积、全等; 两图形全等即经过平移、旋转、对称两 图形重合;而长度、角度、面积经过上 述正交变换保持不变。 ●结论:欧氏几何研究图形在正交变换 下的不变性和不变量

与石扑性质相关的几个例子 >一笔画问题 >哥尼斯堡七桥问题 >四色问题 4
4 与拓扑性质相关的几个例子 ➢一笔画问题 ➢哥尼斯堡七桥问题 ➢四色问题

一笔画问题 平面上由曲线段构成的一个图 形能不能一笔画成,使得在每条线 段上不重复? 例如:日,中可以一笔画出 田,目不能一笔画出 5
5 一笔画问题 平面上由曲线段构成的一个图 形能不能一笔画成,使得在每条线 段上不重复? 例如:日 ,中 可以一笔画出 田 ,目 不能一笔画出

日字的变形 田字的变形 6
6 日 字的变形 田 字的变形

欧拉的结论 欧拉考察了一笔画图形的结构特征。发现, 凡是能用一笔画成的图形,都有这样一个 特点:每当你用笔画一条线进入中间的 个点时,你还必须画一条线离开这个点。 否则,整个图形就不可能用一笔画出。也 就是说,单独考察图中的任何一个点(除 起点和终点外),它都应该与偶数条线相 连;如果起点与终点重合,那么,连这个 点也应该与偶数条线相连
7 欧拉的结论 欧拉考察了一笔画图形的结构特征。发现, 凡是能用一笔画成的图形,都有这样一个 特点:每当你用笔画一条线进入中间的一 个点时,你还必须画一条线离开这个点。 否则,整个图形就不可能用一笔画出。也 就是说,单独考察图中的任何一个点(除 起点和终点外),它都应该与偶数条线相 连;如果起点与终点重合,那么,连这个 点也应该与偶数条线相连

一笔画问题的特点 该问题与线段的长短曲直、交点的准 确方位、面积、体积无关。重要的是 图形中点线之间的相关位置,或相互 连结的情况不能变。 8
8 一笔画问题的特点 该问题与线段的长短曲直、交点的准 确方位、面积、体积无关。重要的是 图形中点线之间的相关位置,或相互 连结的情况不能变

哥尼斯堡七桥问题 到得秀晶系婆罗德鑫鲜金克着资蚊人爽 海。河心有一个小岛。河水把城市分成了4块,于是,人 们建造了7座各具特色的桥,艳哥尼斯堡连成一体。 天又一天,7座桥上走过了无数的行人。不知从什 么时候起,脚下的桥梁触发了人们的灵感,一个有趣的问 题在居苠中传开了:,谁能够二次走遍所有的7座桥,而且 每座标都只通过一次? 这个问题似乎不难,谁都乐意用它来测试一下自己的 幫大兰致鬓谁出遥有投 可是,谁也没有找到一条这样的路线。以博学著称 筹莫展。七桥问题"难往了哥尼 斯堡的所有居民。哥尼斯堡也因"七桥问题"而出了名。 9
9 哥尼斯堡七桥问题 哥尼斯堡是位于波罗的海东岸一座古老而美丽的城市,布 勒格尔河的两条支流在这里汇合,然后横贯全城,流入大 海。河心有一个小岛。河水把城市分成了4块,于是,人 们建造了7座各具特色的桥,把哥尼斯堡连成一体。 一天又一天,7座桥上走过了无数的行人。不知从什 么时候起,脚下的桥梁触发了人们的灵感,一个有趣的问 题在居民中传开了:谁能够一次走遍所有的7座桥,而且 每座桥都只通过一次? 这个问题似乎不难,谁都乐意用它来测试一下自己的 智力。可是,谁也没有找到一条这样的路线。以博学著称 的大学教授们,也感到一筹莫展。"七桥问题"难住了哥尼 斯堡的所有居民。哥尼斯堡也因"七桥问题"而出了名
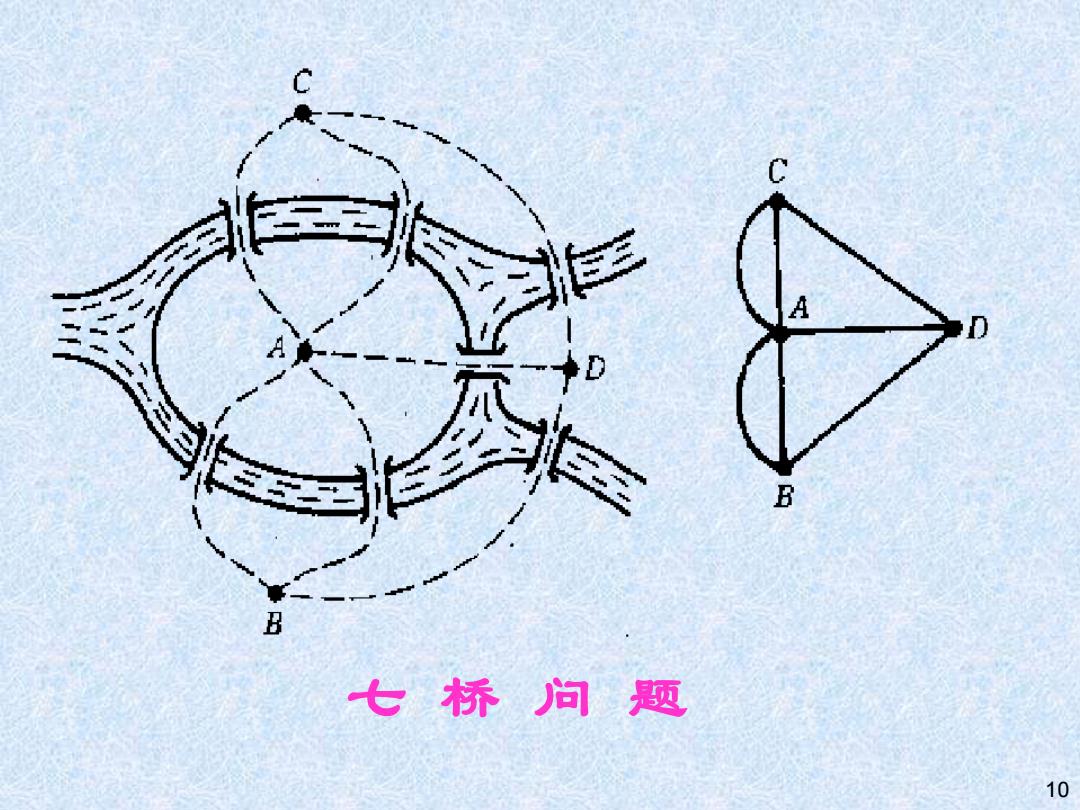
C 三非安三 B B 七桥问题 10
10 七 桥 问 题