
一、指数函数 定义2.5对于复数z=+y,称 w=e:=extis 为指数函数 对于任意实数y, e=cos y+isiny 称为欧拉公式
一、指数函数 cos y sin y y e i i = + 对于任意实数 y , 为指数函数 对于复数 称 z x i y w e e z x iy + = = 定义2.5 = + , 称为欧拉公式

指数函数的性质 1、指数函数=e在整个复平面有定义 在整个复平面是解析且有:(e)'=e 2、当y=0时,e=e,所以w=e是实 变指数函数在复平面上的解析拓广; 3、由定义可知 le-=e* Arge=y+2kr,k=0,±1,±2,. 4、e≠0
变指数函数在复平面上的解析拓广; 2、当y = 0时,e z = e x ,所以w = e z 是实 指数函数的性质 在整个复平面是解析,且有: 1、指数函数w = e z 在整个复平面有定义, z z (e )'= e y k k , , , | | z z x Arge 2 0 1 2 e e = + = = , 3、由定义可知. z 4、e 0

5、若1三x+iy32三2+y一则 e1·e2=e1+2 但e=e的,未必成立,如e月e子 即e无乘幂的意义.与实指数函数的区别之一。 6、w=e是以2kπi为周期的周期函数: et2kri =e.e2kxi =e (cos 2kn+isin2kn)=e. 与实指数函数的区别之二 7、z→o时,w=e无极限, 事实上:lime2=lime=+oo,lime2=limex=0 二->00 X>+00 Z→00 1X>-00 2=x>0 2=x<0
6、w = e z 是以2ki为周期的周期函数: 5、若z1 = x1 + iy1 ,z2 = x2 + iy2 ,则 . z z z 2 1 2 e e + = 1 z e 7、z → 时,w = e z 无极限,(cos k sin k ) . z 2kπ z k z z e e e e 2 i 2 e i 2 i = = + = 即 + lim lim , x x z x z = = + →+ = → e e z 0 事实上: lime lim 0 z 0 = = →− = → x x z x z e 1 2 1 2 1 2 2 ( ) ( ) i z z z z i e e e e − − 但 = ,未必成立,如 z 即 无乘幂的意义.与实指数函数的区别之一。 e 与实指数函数的区别之二

二、对数函数 定义2.6把满足e”=z(z≠0)的函数w=f(z) 称为对数函数,记作w=Lnz. 令w=u+iy,z=re,那么e+iw=re. →u=1nr,y=0+2kπ(k=0,±1,±2,) Lnz In+iArgz In+i(arg=+2k). (k=0,±1,±2,…)
二、对数函数 定义2.6 , . ( ) ( ) w z z z w f z w Ln e 0 = = = 称为对数函数 记作 把满足 的函数 l n , ( 0 1 2 ) , , . , , , 令 那么 = = + = = + = = + u r v k k w u iv z r e e r e i u i v i 2 ( 0 1 2 ) Ln ln i ln i(arg 2 ) k , , , z z z z z k . = = + Arg = + +

由定义可知:w=Lnz是z的无穷多值函数 当Argz取主值argz时,称为Lnz的主值, 记作lnz=lnz+iarg, 这是Lnz的一个单值分支 其余各个分支为: Lnz=lnz+i2kr(k=0,±1,±2,…)
w = Lnz 当Argz取主值argz时,称为Lnz的主值, Ln ln i2 ( 0,1, 2,) 其余各个分支为: z = z + k k = 这是 的一个单值分支 记作 , z z z z Ln ln = ln + iarg 由定义可知: w= Lnz 是 z 的无穷多值函数 的无穷多值函数 的无穷多值函数

例如当z=a>0,na的主值lna(arg=0) Lna=lna+2πik (k=0,±1,±2,…) 当z=-a(a>0)Ln(-a的主值ln(-a)=lna+πi Ln(-a)=lna+(2k+l)元i 特别a=-11n(-1)=1n1+a=ad Ln(-1)=(2k+1)a 注:w=Lnz不仅对正数有意义,对一切非零 复数都有意义.(负数也有对数) 注:在实变函数中,负数无对数,此例说明在复数范 围内不再成立.而且正实数的对数也是无穷多值的.因 此,复变数对数函数是实变数对数函数的拓广
Ln ln 2 i ( 0 1 2 ) 0 Ln ln (arg 0) a a k k , , , z a , a a z = + = 例如 当 = 的主值 = ( a ) a ( k ) i z a( a ) ( a ) ( a ) a i − = + + = − − − = + Ln ln 2 1 当 0 Ln 的主值ln ln Ln k i a i i ( 1) (2 1) 1 ln( 1) l n1 − = + 特别 = − − = + = .(负数也有对数 ) Lnz , 复数都有意义 注:w = 不仅对正数有意义 对一切非零 注:在实变函数中, 负数无对数, 此例说明在复数范 围内不再成立. 而且正实数的对数也是无穷多值的. 因 此, 复变数对数函数是实变数对数函数的拓广

对数函数的性质: (Ln()=Lnz+Lnz,Ln=Lnz-Lnz 22 注:这两个式子两端 都表示集合 等式L=nLnz,Ln√E=Lne.n>l)不成立. n (2)连续性: lnz在除去原点与负实轴外处处连续 因此Lnz的各个分支在复平面上除原点及 负实轴外处处连续
对数函数的性质: 注:这两个式子两端 都表示集合 1 2 2 1 (1) Ln( 1 2 ) Ln 1 Ln 2 Ln Lnz Lnz z z z z = z + z , = − ln . (2) : 在除去原点与负实轴外处处连续 连续性 z . z 负实轴外处处连续 因此Ln 的各个分支在复平面上除原点及 z. ( n ) . n z n z, z n n Ln 1 不成立 1 等式 Ln = Ln Ln =

(3)解析性 lnz在除去原点与负实轴 的平面内解析,且 dw dz dz 7 即- dw 由Lnz=lnz+i2km(k=0,±1,±2,…) 故Lnz的每个分支nz除了原点和负实轴外 均是解析的,且心人=】 今后我们应用对数函数Lnz时,指的都是它在除去原点及 负实轴的平面内的某一单值分支
e z dw dz dz dw w 1 1 1 = = = z z 1 即 (ln )'= 在除去原点与负实轴 的平面内解析 且 解析性 lnz , (3) . z ( z ) ' z ( z ) k k 1 ln Ln ln 均是解析的,且 = 故 的每个分支 除了原点和负实轴外 由Lnz = lnz +i2k ( k = 0,1, 2,) 今后我们应用对数函数Ln z时, 指的都是它在除去原点及 负实轴的平面内的某一单值分支

例1求下列各式的值: (1)Ln(-2+3i);(2)Ln(3-√3i);(3)Ln(-3). 解()Ln(-2+3i) =ln-2+3i+iArg(-2+3i) t3arctanj rk) (k=0,±1,±2,) 9
9 例 1 (1)Ln( 2 3 ); (2)Ln(3 3 ); (3)Ln( 3). : − + i − i − 求下列各式的值 解 (1)Ln ( − 2 + 3 i ) = ln − 2 + 3i + iArg(−2 + 3i)2 . 23 ln13 arctan 21 = + i − + k (k = 0, 1, 2,)
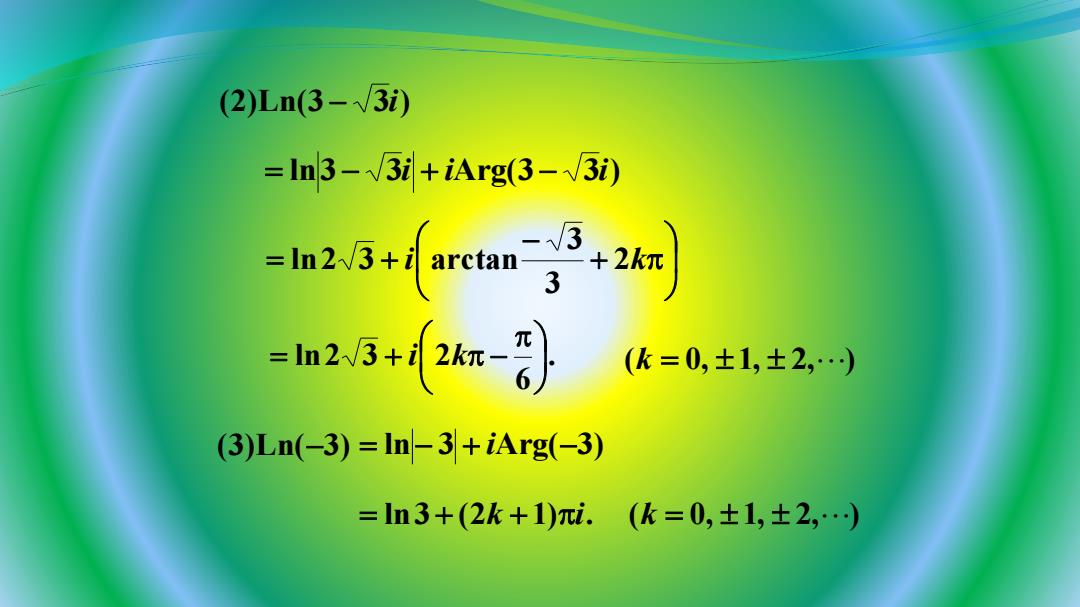
(2)Ln(3-√3) =ln3-√3i+iArg(3-√3动) =h2+arng,2r) =n23+-8 (k=0,±1,士2, 3)Ln(-3)=ln-3+iArg(-3) =ln3+(2k+1)i.(k=0,±1,±2,…)
. 6 ln2 3 2 = + i k − (k = 0, 1, 2, ) (3)Ln(−3) = ln − 3 + iArg(−3) = ln3 + (2k + 1)i. (k = 0, 1, 2, ) (2)Ln(3 − 3i) = ln3 − 3i + iArg(3 − 3i) + − = + i 2k 3 3 ln2 3 arctan