聊城大学：《拓扑学 Topology》课程教学资源（授课教案，孟晗）

点集拓扑学教案 为聊城大学数学科学学院数学与应用数学专业三年级本科生开设《点集拓扑》 课程。 按熊金城《点集拓扑讲义》（第三版，北京：高等教育出版社，2003）第一至七 章编写的教案。 本科生授课64学时，教学内容与进度安排如下： 章 本科生授课主要内容 课时数 备注 节 拓扑学的起源 1 朴素集合论 集合、映射与关系 .1 1 无限集 1 2 拓扑空间与连续映射 21 习题课时2 2 度量空间与连续映射 不讲附录 .1 2 拓扑空间与连续映射 3 .2 2 邻域与邻域系 2 3 不讲定理2.3.3 导集、闭集、闭包内部、边界 % 4 不讲例2.4.4，定理2.4.8 2 内部、边界 3 .5 2 部分证明定理2.6.3，临域基 基与子基 2 6 及相关内容在5.1中介绍 2 拓扑空间中的序列 2 .7 国 子空间、有限积空间、商空间 6 习题课时1 3 子空间 2 .1 3 积空间 2 .2 1

1 点集拓扑学教案 为聊城大学数学科学学院数学与应用数学专业三年级本科生开设《点集拓扑》 课程。 按熊金城《点集拓扑讲义》(第三版, 北京: 高等教育出版社, 2003)第一至七 章编写的教案。 本科生授课 64学时，教学内容与进度安排如下： 章 节 本科生授课主要内容 课时数 备注 拓扑学的起源 1 一 朴素集合论 2 1 .1 集合、映射与关系 1 1 .2 无限集 1 二 拓扑空间与连续映射 21 习题课时 2 2 .1 度量空间与连续映射 3 不讲附录 2 .2 拓扑空间与连续映射 3 2 .3 邻域与邻域系 2 不讲定理 2.3.3 2 .4 导集、闭集、闭包内部、边界 3 不讲例 2.4.4, 定理 2.4.8 2 .5 内部、边界 2 2 .6 基与子基 2 部分证明定理2.6.3，临域基 及相关内容在5.1中介绍 2 .7 拓扑空间中的序列 2 三 子空间、有限积空间、商空间 6 习题课时1 3 .1 子空间 2 3 .2 积空间 2

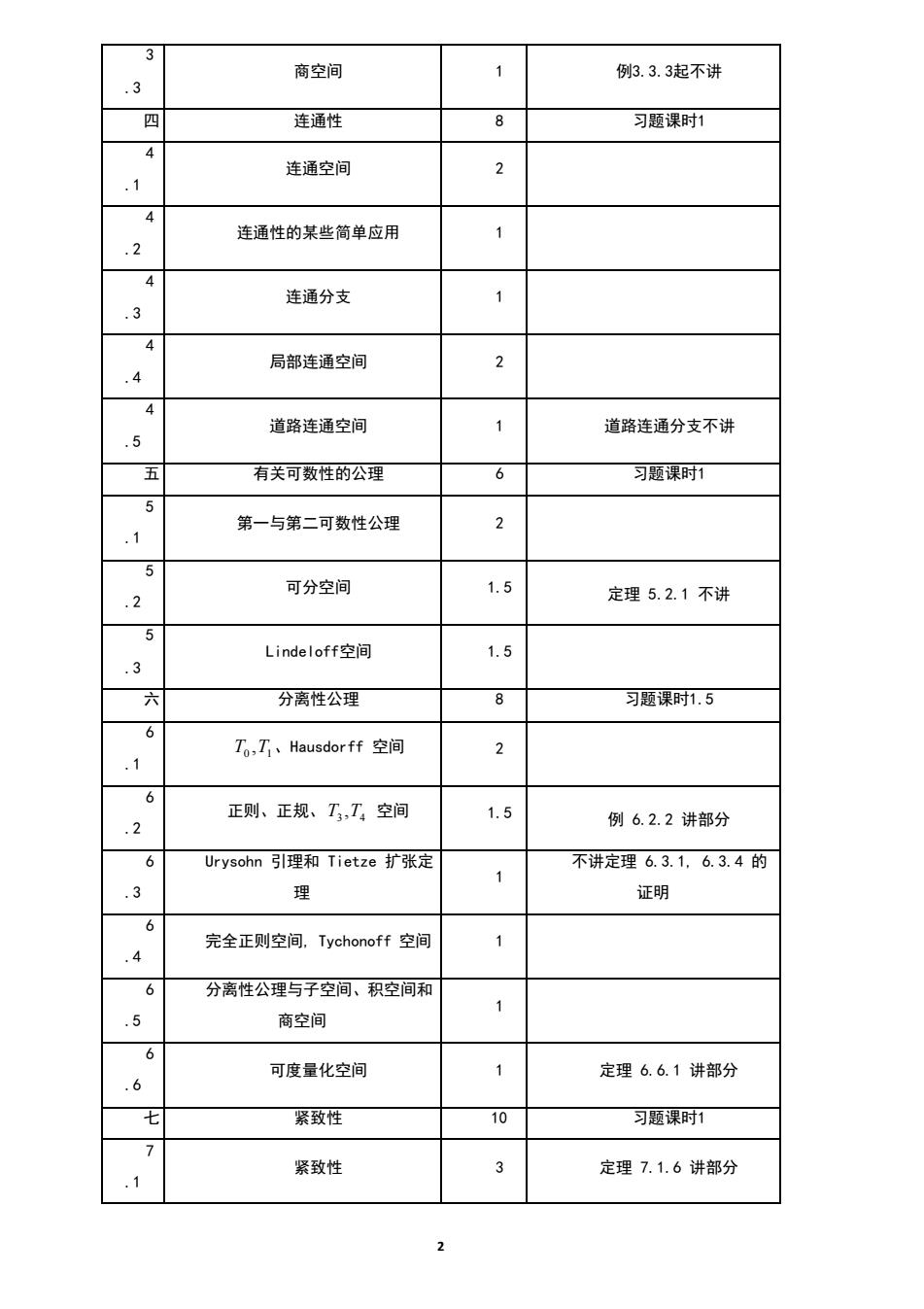
3 商空间 例3.3.3起不讲 3 四 连通性 习题课时1 连通空间 2 .1 4 连通性的某些简单应用 1 .2 4 连通分支 .3 4 局部连通空间 .4 道路连通空间 道路连通分支不讲 .5 7 五 有关可数性的公理 6 习题课时1 5 第一与第二可数性公理 2 .1 5 可分空间 1.5 .2 定理5.2.1不讲 5 Lindeloff空间 1.5 .3 六 分离性公理 8 习题课时1.5 6 T,I、Hausdorff空间 2 .1 正则、正规、T,工4空间 1.5 .2 例6.2.2讲部分 Urysohn引理和Tietze扩张定 不讲定理6.3.1,6.3.4的 1 3 理 证明 完全正则空间，Tychonoff空间 .4 6 分离性公理与子空间、积空间和 1 .5 商空间 6 可度量化空间 定理6.6.1讲部分 .6 七 紧致性 10 习题课时1 7 紧致性 3 定理7.1.6讲部分 .1 2

2 3 .3 商空间 1 例3.3.3起不讲 四 连通性 8 习题课时1 4 .1 连通空间 2 4 .2 连通性的某些简单应用 1 4 .3 连通分支 1 4 .4 局部连通空间 2 4 .5 道路连通空间 1 道路连通分支不讲 五 有关可数性的公理 6 习题课时1 5 .1 第一与第二可数性公理 2 5 .2 可分空间 1.5 定理 5.2.1 不讲 5 .3 Lindeloff空间 1.5 六 分离性公理 8 习题课时1.5 6 .1 0 1 T ,T 、Hausdorff 空间 2 6 .2 正则、正规、 3 4 T ,T 空间 1.5 例 6.2.2 讲部分 6 .3 Urysohn 引理和 Tietze 扩张定 理 1 不讲定理 6.3.1, 6.3.4 的 证明 6 .4 完全正则空间, Tychonoff 空间 1 6 .5 分离性公理与子空间、积空间和 商空间 1 6 .6 可度量化空间 1 定理 6.6.1 讲部分 七 紧致性 10 习题课时1 7 .1 紧致性 3 定理 7.1.6 讲部分

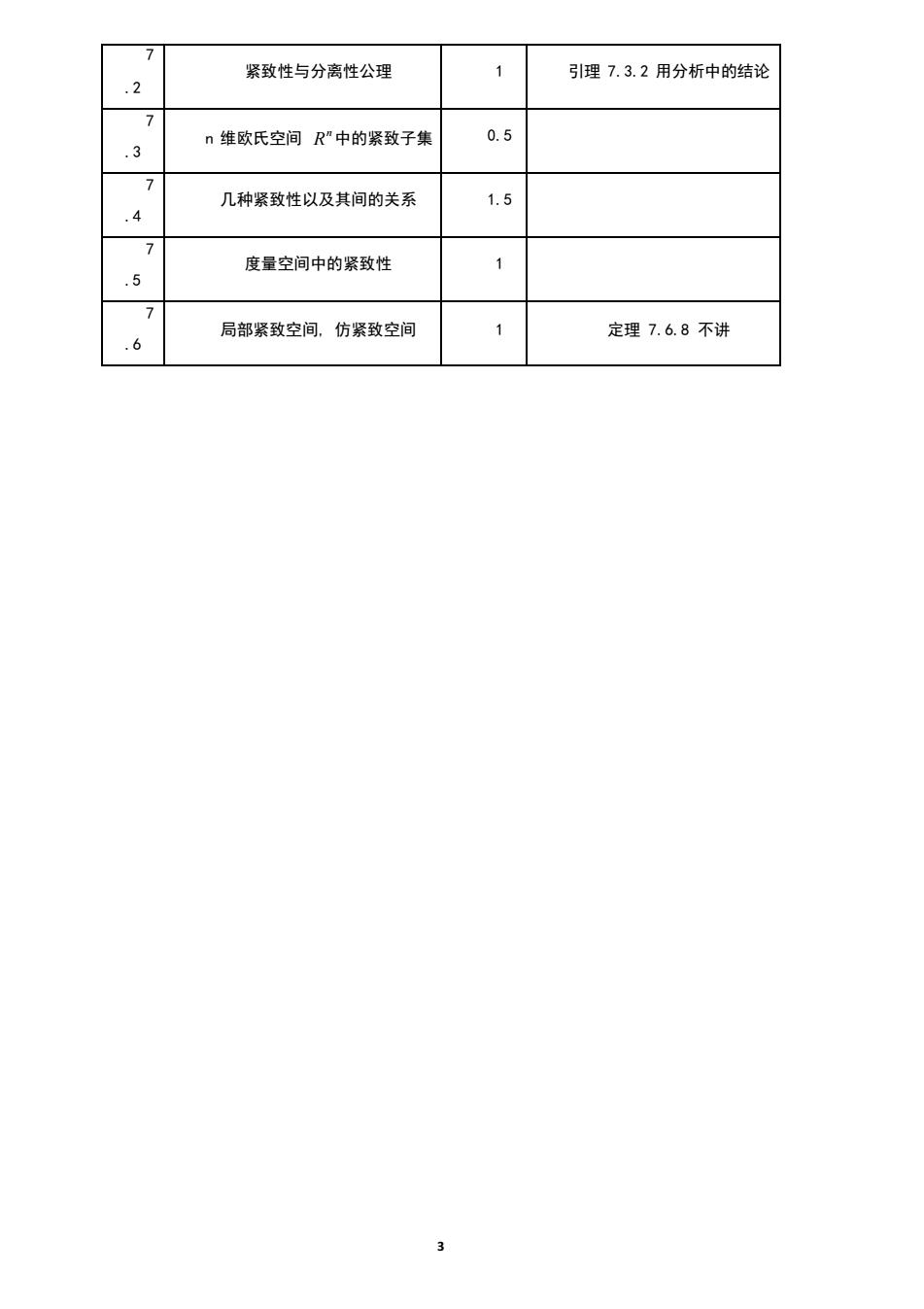
紧致性与分离性公理 引理7.3.2用分析中的结论 .2 n维欧氏空间R”中的紧致子集 0.5 .3 几种紧致性以及其间的关系 1.5 7 度量空间中的紧致性 .5 局部紧致空间，仿紧致空间 1 定理7.6.8不讲 .6

3 7 .2 紧致性与分离性公理 1 引理 7.3.2 用分析中的结论 7 .3 n 维欧氏空间 n R 中的紧致子集 0.5 7 .4 几种紧致性以及其间的关系 1.5 7 .5 度量空间中的紧致性 1 7 .6 局部紧致空间, 仿紧致空间 1 定理 7.6.8 不讲

第一章朴素集合论 点集拓扑学(Point-set Topology)现称一般拓扑学General Topology),它的起源与出发点都 是集合论.作为基本的点集拓扑学知识，所需的只是一些朴素集合论的预备知识.本章介绍本 书中要用到的一些集合论内容，主要涉及集合及集族的运算、等价关系、映射、可数集、选 择公理等.作为一教材，讲义对各部分内容均有较系统的论述，作为授课，我们只强调一些基 本内容，而对已有过了解的知识不提或少提 记号：乙，Z+,R,Q分别表示整数集，正整数集，实数集和有理数集 教学重点：集合的基本概念、运算，映射的概念；教学难点：选择公理 一.集合的运算 幂集P(X),交n、并U、差-（补，余A,A) 运算律：De Morgan律：(I)A-(BUC)=(A-B)⌒(A-C) (2)A-(BC)=(A-B)(A-C)A-(Bn C)=(A-B)U(A-C) 利用集合的包含关系证明(1) 类似可定义任意有限个集的交或并，如记 AUA,U.UA=(4UUA)UA。=UA,=U4A.规定0个集之并是 中，不用0个集之交 二关系 R是集合X的一个关系，即RCX×X,(x,y)∈R记为xRy,称x与y是R相关的 R称为自反的，若X∈X,xRx R称为对称的，若xRy,则yRx R称为传递的，若xRy,yRz,则xRz 等价关系：自反、对称、传递的关系」 如，△(X={(Xx)x∈X,恒同关系，它是等价关系，{Xy)川xy∈R,x<y},小于关系， 它是传递的，但不是对称的、不是自反的 设R是X上等价关系，X∈X,x的R等价类或等价类[x內R或x为y∈X|xRy}, [☒R的元称为[內R的代表元；商集XR={[R|x∈X 定理1.4.1设R是非空集合X的等价关系，则

4 第一章 朴素集合论 点集拓扑学(Point-set Topology)现称一般拓扑学(General Topology), 它的起源与出发点都 是 集合论. 作为基本的点集拓扑学知识, 所需的只是一些朴素集合论的预备知识. 本章介绍本 书中 要用到的一些集合论内容, 主要涉及集合及集族的运算、等价关系、映射、可数集、选 择公理等. 作为一教材, 讲义对各部分内容均有较系统的论述 , 作为授课, 我们只强调一些基 本内容, 而对 已有过了解的知识不提或少提. 记号: Z, Z+, R, Q 分别表示整数集, 正整数集, 实数集和有理数集. 教学重点：集合的基本概念、运算，映射的概念；教学难点：选择公理 一. 集合的运算 幂集 P (X ), 交∩ 、并∪、差－(补, 余 / A , A c ). 运算律: De Morgan 律: (1) A -(B  C) = (A - B)  (A -C). (2) A -(B  C) = (A - B)  (A -C) A-(B∩ C)=(A-B)∪(A-C) 利用集合的包含关系证明(1). 类似可定义任意有限个集的交或并, 如记 i n  n i A A An A An An Ai Ai  =    =   −  = = 1 1 2 1 1 ... ( ... ) Ai. 规定 0 个集之并是  , 不用 0 个集之交. 二. 关系 R 是集合 X 的一个关系, 即 R  X  X ,(x, y)  R 记为 xRy , 称 x 与 y 是 R 相关的. R 称为自反的, 若 x  X , xRx; R 称为对称的, 若 xRy, 则 yRx; R 称为传递的, 若 xRy, yRz, 则 xRz. 等价关系: 自反、对称、传递的关系. 如, Δ(X)={(x, x )|x  X}, 恒同关系, 它是等价关系; {(x, y) | x, y  R, x  y}，小于关系, 它是传递 的, 但不是对称的、不是自反的. 设 R 是 X 上等价关系, x  X , x 的 R 等价类或等价类 R [x] 或[x]为 {y  X| xRy} , R [x] 的元称为 R [x] 的代表元; 商集 X/R = {[x]R | x  X} . 定理 1.4.1 设 R 是非空集合 X 的等价关系, 则

(I)x∈XX∈[☒R; (2)Xy∈X,或者xR=y]R,或者[內R∩yR=中 证(2).设z∈內R∩)R,则ZR,z乃，于是[NRC]R且內R一R,于是 [☒R=yR 三.映射 函数：f:X→Y 像：AcX,f(A)={f(x)川x∈A: 原像：HBcY,f(B)={x∈Xf(x)∈B) 满射、单射、一一映射（双射）、可逆映射、常值映射、恒同映射ix、限制4、扩张、内 射iy4A→X 集合X,i≤n,笛卡儿积 X×X2×.×Xn=∏snX,=X,={《x,x2xnx∈X,i≤m到第i个坐标集X, 的投射p,:X→X,定义为p(x)=x,其中x=(x1,,xn) 对等价关系R,集合X到商集XIR的自然投射p:X→X/R定义为p(x)=[x]R 四.集族 数列xn}={xn}n2,有标集族{A,}yer,指标集「，与{A,y∈t}不同，可记有标集族 A={A,}A;类似地，定义其并U,A:(或UA)、交∩e,A:(或nA,不定义0个集的交.与 有限集族有相同的运算律，如De Morgan律 A-U4,=∩(4-A,)bA-∩e,4=U,eA, 映射对应的集族性质：fU,A,)=UE,f(A,)bf(∩e,A,)=∩e,f(4,), f-UB,)=U,-(B,bf-(∩B,)=∩ef-(B,) 五.无限集 通过一一映射来确定两集合的个数的多少 有限集(p或与某{1,2，…，}有一一映射)，无限集，可数集（φ或存在X到Z+的单射），不可 数集 易验证：有限集是可数集，可数集的子集是可数集，可数集的映像是可数集， 定理1.7.3X是可数集台X是Z+的映像 5

5 (1) R x X, x [x] ; (2) x, y  X ，或者[x]R =[y]R , 或者 [x]R [y]R =  证(2). 设 R R z[x] [y] , 则 ZRx,zRy , 于是 R R [x]  [y] 且 R R [x]  [y] , 于是 R R [x] = [y] . 三. 映射 函数： f : X → Y . 像： A  X, f (A) = { f (x) | x  A} ； 原像： , ( ) { | ( ) } B  Y f −1 B = x X f x B 满射、单射、一一映射(双射)、可逆映射、常值映射、恒同映射 X i 、限制 A f | 、扩张、内 射 iX |A:A → X 集合 Xi ,i  n , 笛卡儿积   =    = = =   n i i n i i i n X X Xn Xi X x x x x X i n 1 1 2 1 1 2 ... {( , ... ) , } 到第 i 个坐标集 Xi 的投射 pi X → Xi : 定义为 i p(x) =x , 其中 ( ,.., ) 1 n x = x x . 对等价关系 R, 集合 X 到商集 X / R 的自然投射 p : X → X / R 定义为 R p(x) = [x] . 四. 集族 数列  + n = n n Z {x } {x } , 有标集族   {A } , 指标集 Γ, 与 {  } A  不同, 可记有标集族 A = A A { } ; 类似地, 定义其并   A (或∪A)、交   A (或∩ A), 不定义 0 个集的交. 与 有限集族有相同的运 算律, 如 De Morgan 律                   A − A = (A − A ), A − A = A , 映射对应的集族性质:                   f ( A ) = f (A ), f ( A ) = f (A ) ,                 −   − −  − ( ) = ( ), ( ) = ( ) 1 1 1 1 f B f B f B f B 五. 无限集 通过一一映射来确定两集合的个数的多少. 有限集(  或与某{1, 2, … , n}有一一映射), 无限集, 可数集(  或存在 X 到 Z+的单射),不可 数集. 易验证: 有限集是可数集, 可数集的子集是可数集, 可数集的映像是可数集. 定理 1.7.3 X 是可数集  X 是 Z+的映像

由此，Q是可数集，两可数集的笛卡儿积集是可数集，可数个可数集之并集是可数集 定理1.7.8R是不可数集 利用Cantor对角线法证明开区间(0,1)中的实数不可数 直观上，集合A中元素的个数称为该集合的基数，记为card A或A.亿+=a,RFc.若存 在从集合A到集合B的单射，则定义A≤B, 连续统假设：不存在基数，使得aB 6

6 由此, Q 是可数集, 两可数集的笛卡儿积集是可数集, 可数个可数集之并集是可数集. 定理 1.7.8 R 是不可数集. 利用 Cantor 对角线法证明开区间(0, 1)中的实数不可数 . 直观上, 集合 A中元素的个数称为该集合的基数, 记为card A, 或|A|. |Z+|= a , |R|= c . 若存 在 从集合 A 到集合 B 的单射, 则定义|A|≤ |B|. 连续统假设: 不存在基数  , 使得 a   c . 选择公理: 若 A 是由非空集构成的集族, 则 A A, 可取定  (A)  A. . 由选择公理可证明, 若 , 是基数, 则下述三式中有且仅有一成立:   , = ,  

第二章拓扑空间与连续映射 本章是点集拓扑学基础中之基础，从度量空间及其连续映射导入一般拓扑学中最基本的 两个概念：拓扑空间、连续映射，分析了拓扑空间中的开集、邻域、聚点、闭集、闭包、内 部、边界、基与子基的性质，各几种不同的角度生成拓扑空间，及刻画拓扑空间上的连续性 教学重点：拓扑空间与连续映射，邻域与邻域系； 教学难点：基与子基；可度量化空间 2.1度量空间与连续映射 在R上，xy表示点x与y之间的距离.绝对值是一非负函数，具有三条重要性质 定义2.11设X是一集合，p:X×X→R.如果满足正定性、对称性和三角不等 式，则称p是X的一个度量.(X,p)称为度量空间，p(Xy)表示两点xy之间的距离. 例2.1.1实数空间R (Xy)k-y儿，R的通常度量. 例2.1.2n维欧氏空间R”=R×R×.×R 对于x∈R”,记x=(x;)1sism定义P(x,y x-y)2 为Rm的通常度量，n维欧 氏空间.R2称为欧氏平面或平面. 例2.1.3 Hilbert空间H. H={x=(x,x2x x20,使得不存在X中的点y≠x,满足 p(x,y)<6如对集合X,按如下方式定义p:X×X→R是X上的离散度量： 0,x=y p(x,y)= 1,x≠y 定义2.1.2设(X,P)是度量空间Bx,)=y∈XP(x,)<称为以x为心，E为半径

7 第二章 拓扑空间与连续映射 本章是点集拓扑学基础中之基础, 从度量空间及其连续映射导入一般拓扑学中最基本的 两 个概念: 拓扑空间、连续映射, 分析了拓扑空间中的开集、邻域、聚点、闭集、闭包、内 部、边 界、基与子基的性质，各几种不同的角度生成拓扑空间，及刻画拓扑空间上的连续性. 教学重点：拓扑空间与连续映射,邻域与邻域系； 教学难点：基与子基；可度量化空间 2.1 度量空间与连续映射 在 R 上, |x-y|表示点 x 与 y 之间的距离. 绝对值是一非负函数, 具有三条重要性质. 定义 2.1.1 设 X 是一集合 ,  : X  X → R . 如果 满足正定性、对称性和三角不等 式, 则称  是 X 的一个度量. (X , ) 称为度量空间, (x, y) 表示两点 x, y 之间的距离. 例 2.1.1 实数空间 R. (x,y)=|x -y|, R 的通常度量. 例 2.1.2 n 维欧氏空间 R R R R n =  ... . 对于 n x  R , 记 i i n x x = 1  ( ) 定义 = = − n i i i x y x y 1 2 ( , ) ( ) 为 Rn 的通常度量, n 维欧 氏空间. R2 称为欧氏平面或平面. 例 2.1.3 Hilbert 空间 H. { ( , ,.. ...) }, 1 2 1 2   = = =   i n i H x x x x x   = → = −  → 1 2 ( , ) ( , ) ( ) : i i i x y x y x y H H R  定义 , 易证  为度量 则度量空间 (H, ) 称为 Hilbert 空 间. 例 2.1.4 离散度量空间. 度量空间 (X , ) 称为离散的, 若 x  X, x  0 , 使得不存在 X 中的点 y  x , 满足 x (x, y)   如对集合 X , 按如 下方式定 义  : X  X → R 是 X 上的离散度 量:     = = x y x y x y 1, 0, ( , ) 定义2.1.2 设 (X , ) 是度量空间 B(x, ) ={y  X (x, y)  } 称为以x为心, 为半径

的球形邻域或ε邻域，或球形邻域.对R,),B(XE)=(X-6,x+). 定理2.1.1度量空间(X,P)的球形邻域具有性质： (1)x∈X,&>0,x∈B(xE) (2) x∈X,61,62>0,则归63>0，满足x∈B(x,6)CBx,6)nB(x,82,): (3)若y∈B(x,6,36>0使B(,)CB(x,): 证(2)00,使B(x,8)CA.每一球 形邻域是开集. 例2.1.5R中的开区间是开集 x∈(a,b)让￡=min{x-a,b-x}则B(x,)s(a,b)同样可证，无限开区也是开集. 闭区间[a,b)不是开集. 定理2.1.2度量空间的开集具有以下性质： (1)X,中是开集；(2)两开集的交是开集；(3)任意开集族之并是开集 证(1)由定理2.1.1(1)(2)，(3)由定理2.1.1(2). 定义2.1.4设X是度量空间，x∈X,U三X,U称为x的邻域，若有开集V,使 x∈VsU. 定理2.1.3U是X中点x的邻域存在ε>0，使B(x,c)cU. 定义2.1.5设X,Y是两度量空间.f:X→Y,x。∈X,称f在x。连续，若f(xo) 的球形邻域B(f(x,),),(&>O) 存在x。的球形邻域B(xo,δ)，使f(B(xo,δ)CB(f(x),), 称∫在X连续，若f在X的每一点连续。 定理2.1.4设X,Y是两度量空间.f:X→Y,x。∈X,那么 (I)f在x。连续若U是f(x)的邻域，则∫-(U)是x。的邻域： (2)∫在X连续若U是Y的开集，则f-(U)是X的开集

8 的球形邻域或  邻域, 或球形邻域. 对(R, |.|), B(x,  ) = (x -  , x +  ). 定理 2.1.1 度量空间 (X , ) 的球形邻域具有性质: (1) x  X,  0, x  B(x. ) (2) , , 0, 0, ( ,. ) ( ,. ) ( ,. 2 ) 1 2 3 3 1 3 x  X    则  满足x  B x   B x   B x  ； (3) 若 y  B(x, ),  0 使 B( y, )  B(x, ) ； 证 (2) 0 min{ , } 3 1 2      ； (3)  =  − (x, y),则B(y,)  B(x,) 定义 2.1.3 X 的子集 A 称为 (X , ) 的开集, 若 a A,  0,使B(x,)  A. 每一球 形邻域是开集. 例 2.1.5 R 中的开区间是开集. x  (a,b) 让  = min{ x − a,b − x} 则 B(x, )  (a,b) 同样可证, 无限开区也是开集. 闭区间[a, b] 不是开集. 定理 2.1.2 度量空间的开集具有以下性质: (1) X, 是开集; (2)两开集的交是开集; (3)任意开集族之并是开集. 证 (1)由定理 2.1.1(1); (2), (3)由定理 2.1.1(2). 定义 2.1.4 设 X 是度量空间, x  X,U  X,U 称为 x 的邻域, 若 有开集 V , 使 x V  U . 定理 2.1.3 U 是 X 中点 x 的邻域 存在ε>0, 使 B(x, ε)  U. 定义 2.1.5 设 X ,Y 是两度量空间. f : X → Y , x0  X , 称 f 在 0 x 连续, 若 ( ) 0 f x 的球形邻域 ( ( ), ),( 0) B f x0    存在 0 x 的球形邻域 B(x0, δ), 使 ( ( , )) ( ( ), ). 0 0 f B x   B f x  称 f 在 X 连续, 若 f 在 X 的每一点连续. 定理 2.1.4 设 X ,Y 是两度量空间. f : X → Y , x0  X , 那么 (1) f 在 0 x 连续 若 U 是 ( ) 0 f x 的邻域, 则 ( ) 1 f U − 是 0 x 的邻域; (2) f 在 X 连续 若 U 是 Y 的开集, 则 ( ) 1 f U − 是 X 的开集

证(1)利用定义2.1.5,2.1.4 (2)“”f(U)是每一点的邻域“”证每一点连续，利用(1) 由此可见，度量空间的连续只与邻域或开集有关.它导入建立比度量空间更一般的拓扑空 间的概念及其连续性 9

9 证 (1)利用定义 2.1.5, 2.1.4. (2)“ ”f -1 (U)是每一点的邻域.“ ”证每一点连续, 利用(1). 由此可见, 度量空间的连续只与邻域或开集有关. 它导入建立比度量空间更一般的拓扑空 间 的概念及其连续性

2.2拓扑空间与连续映射 定义2.2.1设x是集合X的子集族，若x满足 ()X,p∈t,(2)HA,B∈t→AnB∈E(3)H1ct,U1∈t 称T是X的一个拓扑(X,x)是拓扑空间，π的元称为X的开集. 空间X的拓扑是X的全体开集的族。 定义2.22(X,p)度量空间.t。由X的所有开集构成的族.(X,t。)称为由度量p诱导出的 拓扑空间.T。简称为度量拓扑 度量空间一定是拓扑空间 例2.2.1平庸拓扑x={X,}平庸空间 例2.2.2离散拓扑t=P(X).离散空间.X的每一子集是开集.由离散度量空间导出的 拓扑是离散拓扑 例2.2.4有限补拓扑π={UcXU'是X的有限子集}U{} 验证T是X上的拓扑.(1)显然.(2)A,BcX,讨论A∩B时分两种情形，一是A,B中 有一是中，二是A,B都不是：(3)T1CT,不妨设3中≠A6∈t1利用De Morgan律.有限 补空间 例2.2.5可数补拓扑π={UcXU'是X的可数子集}U{} 定义2.2.3可度量化空间. 离散空间是可度量化空间.多于一点的平庸空间不是可度量化空间.度量化问题是点集拓 扑学研究的中心问题之一.本书将在6.6中给出该问题的一个经典的解 定义2.2.4X,Y是两拓扑空间.f:X→Y称f连续，若Y中每一开集U的原象(U) 是X中的开集 定理2.2.1恒同映射连续.连续函数的复合是连续的 定义2.2.5f:X→Y称为同胚或同胚映射，若ff是一一映射且ff及f-1均连续 定义2.2.6称两空间X与Y同胚，或X同胚于Y,若存在从X到Y的同胚 定理2.2.2(2.2.3)恒同映射同胚(X与X同胚)；f同胚→f-1同胚（若X与Y同胚，则Y 与X同胚)：同胚的复合是同胚（若X与Y同胚，且Y与Z同胚，则X与Z同胚） 空间的同胚关系是等价关系 10

10 2.2 拓扑空间与连续映射 定义 2.2.1 设  是集合 X 的子集族, 若  满足:            1 1 (1)X, ;(2) A, B A B ;(3) , 称  是 X 的 一 个 拓 扑 (X , ) 是 拓 扑 空 间 ,  的 元 称 为 X 的开集 . 空间 X 的拓扑是 X 的全体开集的族. 定义 2.2.2 (X , ) 度量空间.   由 X 的所有开集构成的族 . (X,   )称为由度量  诱导出的 拓扑空间.   简称为度量拓扑. 度量空间一定是拓扑空间. 例 2.2.1 平庸拓扑  = {X,} 平庸空间. 例 2.2.2 离散拓扑  = P(X ). 离散空间. X 的每一子集是开集. 由离散度量空间导出的 拓扑是 离散拓扑. 例 2.2.4 有限补拓扑 { } { } /  = U  X U 是X的有限子集   . 验证  是 X 上的拓扑. (1)显然 . (2) A, B  X ， 讨论 A∩B 时分两种情形, 一是 A, B 中 有一是  , 二是 A, B都不是  ；（3）   1 ,不妨设 0 1   A  利用 De Morgan 律.有限 补空间. 例 2.2.5 可数补拓扑 { } { } /  = U  X U 是X的可数子集   定义 2.2.3 可度量化空间. 离散空间是可度量化空间. 多于一点的平庸空间不是可度量化空间. 度量化问题是点集拓 扑学研究的中心问题之一. 本书将在6.6中给出该问题的一个经典的解 . 定义 2.2.4 X ,Y 是两拓扑空间. f : X → Y 称 f 连续, 若 Y 中每一开集 U 的原象 f -1 (U) 是 X 中的开集. 定理 2.2.1 恒同映射连续. 连续函数的复合是连续的. 定义 2.2.5 f : X → Y 称为同胚或同胚映射, 若 f f是一一映射且 f f及 −1 f 均连续. 定义 2.2.6 称两空间 X 与 Y 同胚, 或 X 同胚于 Y, 若存在从 X 到 Y 的同胚. 定理 2.2.2(2.2.3) 恒同映射同胚(X 与 X 同胚); f 同胚  −1 f 同胚 (若 X 与 Y 同胚, 则 Y 与 X 同 胚); 同胚的复合是同胚(若 X 与 Y 同胚, 且 Y 与 Z 同胚, 则 X 与 Z 同胚). 空间的同胚关系是等价关系