
【IP 复变品数写积分变换
复变函数与积分变换

第一章复数与复变函数 【I步 复数及其代数运算 复数的表示 复数的乘幂与方根 复平面点集与区域 复变函数 复变函数的极限与连续
第一章 复数与复变函数 复数及其代数运算 复数的表示 复数的乘幂与方根 复平面点集与区域 复变函数 复变函数的极限与连续

复数:形为=x+iy的数称为复数。 x,y为实数,i为虚数单位,2=-1 【I 1)实部Rez=x;虚部Imz=y 2)复数无大小 3)复数相等:设21=x1+y1,22=x2+y2 则:21=22台水=x2,=2 4)复数、实数、虚数的关系
i为虚数单位, 复数:形为 z=x+ i y的数称为复数。 x, y 为实数, 1 2 i = − 1)实部Rez=x;虚部Imz=y 2)复数无大小 3)复数相等:设 则: 1 1 1 2 2 2 z = x +iy ,z = x +iy 1 2 1 2 1 2 z = z x = x , y = y 4)复数、实数、虚数的关系

复平面 一 对有序实 数(x,y) 功 平面上一点P,向量 复数z=x+iy 实轴、虚轴、复平面 z=x+iy Z平面、w平面 X
复平面 一对有序实 数(x,y) 平面上一点P,向量 复数 z = x + i y x y z = x + i y O 实轴、 虚轴、复平面 Z 平面、 w 平面 → op

复数的模 r=z到 【P 复数的幅角 0 Arg 1)z=0的辐角不定 2)主辐角-π<0≤π 3)辐角0=Arctan2 X 4)辐角有无穷多个
复数的 模 r = z 复数的 幅角 = Arg z 1)z=0的辐角不定 2)主辐角 3)辐角 4) 辐角有无穷多个 - rctan y A x =

复数的三角形式与指数形式 x rcos0 y=rsinθ 利用极坐标来表示复数z, r=vx2+y2 则复数z可表示为: 0=Arctan 三角式:z=r(cos0+isin) X 指数式:
复数的三角形式与指数形式 利用极坐标来表示复数z, = = sin cos y r x r 2 2 rctan r x y y A x = + = 则复数 z 可表示为: 三角式: z = r(cos + isin ) i 指数式: z = re

复数的四则运算 规定:z1+22=(x1+x2)+(y1+y2) z122=(x1x2-y1y2)+i(x1y2+y1x2) 1=+少1= x1+y1x2-y2 22 x2+y2 2+y2x2-y2 (x x2+yiy2)+i(x2y-xy2) 2 2 x2+y2 按上述定义容易验证加法交换律、结合律 乘法交换律、结合律和分配律均成立
复数的四则运算 规定: ( ) ( ) 1 2 1 2 1 2 z + z = x + x +i y + y ( ) ( ) 1 2 1 2 1 2 1 2 1 2 z z = x x − y y +i x y + y x 2 2 1 1 2 1 x iy x iy z z + + = 2 2 2 2 2 2 1 1 x iy x iy x iy x iy − − + + = ( ) ( ) 2 2 2 2 1 2 1 2 2 1 1 2 x y x x y y i x y x y + + + − = b) 按上述定义容易验证 加法交换律、结合律 乘法交换律、结合律和分配律均成立
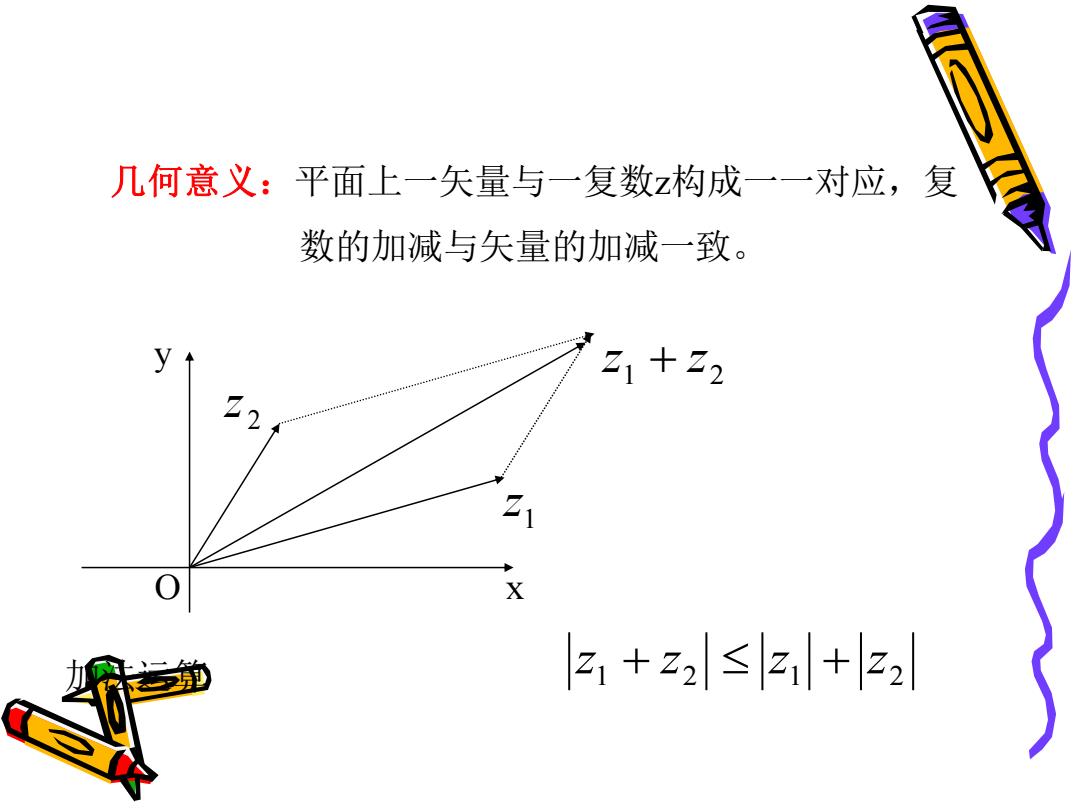
几何意义:平面上一矢量与一复数z构成一一对应,复 数的加减与矢量的加减一致。 y 21+22 12 Z X 2+z2≤z1+22
几何意义:平面上一矢量与一复数z构成一一对应,复 数的加减与矢量的加减一致。 x y O 1 2 z + z 1 z 2 z 1 2 1 2 加法运算 z + z z + z
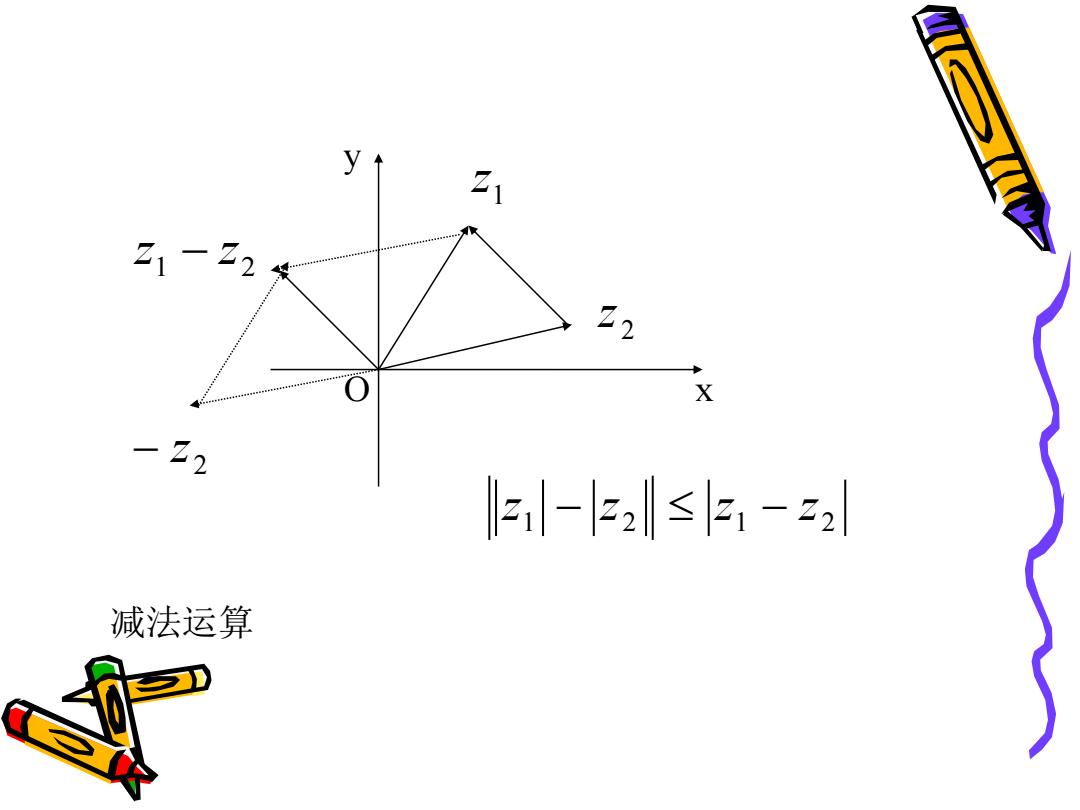
y 21 L【IP 21 一 72 22 X -22 l2-2≤31-2 减法运算
x y O 1 2 z − z 1 z 2 z 2 − z 1 2 1 2 z − z z − z 减法运算

复数乘法 【一IP 设z1=r(cos8+isin0), z2 =r (cos2 +isin 02) z1z2 =rz (cose +isin )(cos +isin 2) =r[cos(8,+82)+isin(8,+82)]
复数乘法 设 (cos sin ), 1 1 1 1 z = r +i (cos sin ) 2 2 2 2 z = r +i (cos sin )(cos sin ) 1 2 1 2 1 1 2 2 z z = rr +i +i [cos( ) sin( )] = 1 2 1 + 2 + 1 + 2 rr i