
一、主要定理和定义 1.两个主要定理: 定理一 如果函数f(z)在单连通域B内处处解析, 那末积分∫f(z)dz与连结起点及终点的路线 C无关 由定理一可知: 解析函数在单连通域内的积分只与起点和 终点有美,(如下页图) 2:44:26
一、主要定理和定义 定理一 ( ) , ( )d . C f z B f z z C 如果函数 在单连通域 内处处解析 那末积分 与连结起点及终点的路线 无关 由定理一可知: 解析函数在单连通域内的积分只与起点和 终点有关, (如下页图) 1. 两个主要定理:
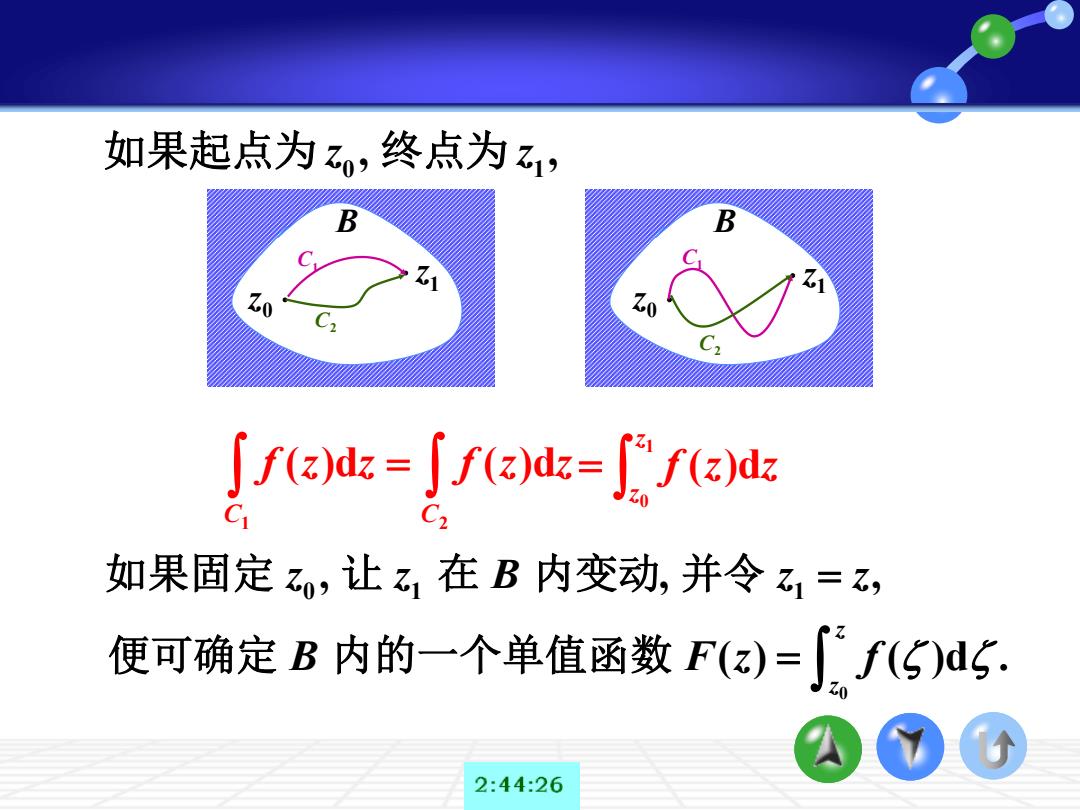
如果起点为z0,终点为乙1, B B 10 fzdk=∫fd=fzdz C C 如果固定,让乙1在B内变动,并令乙1=乙, 便可确定B内的一个单值函数F(a)=」f(5)dG. 2:44:26
B B 0 z 1 z 0 z 1 z C1 C2 C1 C2 0 1 如果起点为 , , z z 终点为 = 1 2 ( )d ( )d C C f z z f z z = 1 0 ( )d z z f z z 0 1 1 如果固定 , , , z z B z z 让 在 内变动 并令 = 0 ( ) ( )d . z z B F z f = 便可确定 内的一个单值函数

定理二 如果函数f(z)在单连通域B内处处解析, 那末函数F(z)=if(5)d5必为B内的一个解 析函数,并且F'(z)=f(z). 证 利用导数的定义来证, 设z为B内任一点, . 以z为中心作一含于B内的 小圆K, 2:44:26
0 ( ) , ( ) ( )d , ( ) ( ). z z f z B F z f B F z f z = = 如果函数 在单连通域 内处处解析 那末函数 必为 内的一个解 析函数 并且 定理二 证 利用导数的定义来证. B 设 , z B 为 内任一点 z , z B K 以 为中心作一含于 内的 小圆 K

取△z充分小使z+△z在K内,由F(z)的定义, F(z+Az)-F(z)-f(5)d-[f(6)ds 由于积分与路线无关, 155的积分路线可先取云到:, (注意:这一段与「f(5)d5的 路线相同) 然后从z沿直线到z+△z, 2:44:26
B z K 取 , + z z z K 充分小使 在 内 z + z F(z + z) − F(z) = − + z z z z z f f 0 0 ( )d ( )d 由于积分与路线无关, 0 0 ( )d , z z z f z z + 的积分路线可先取 到 然后从 z 沿直线到 z + z, 0 z • 0 ( : ( )d ) z z f 注意 这一段与 的 路线相同 由 ( ) , F z 的定义

于是F(z+A)-F(a)=f5)d5, 因为∫tfed5=fe∫td5=fa)Az, 所以 F(a+△z-F②-f() △z (- B &V)-feIac 2:44:26
于是 ( ) ( ) F z z F z + − = ( )d , z+z z f ( )d z z z f z + = 因为 z+z z f (z) d = f (z)z, B z K z + z 0 z • ( ) ( ) ( ) F z z F z f z z + − − 所以 ( )d ( ) 1 f f z z z z z − = + [ ( ) ( )]d 1 f f z z z z z − = +
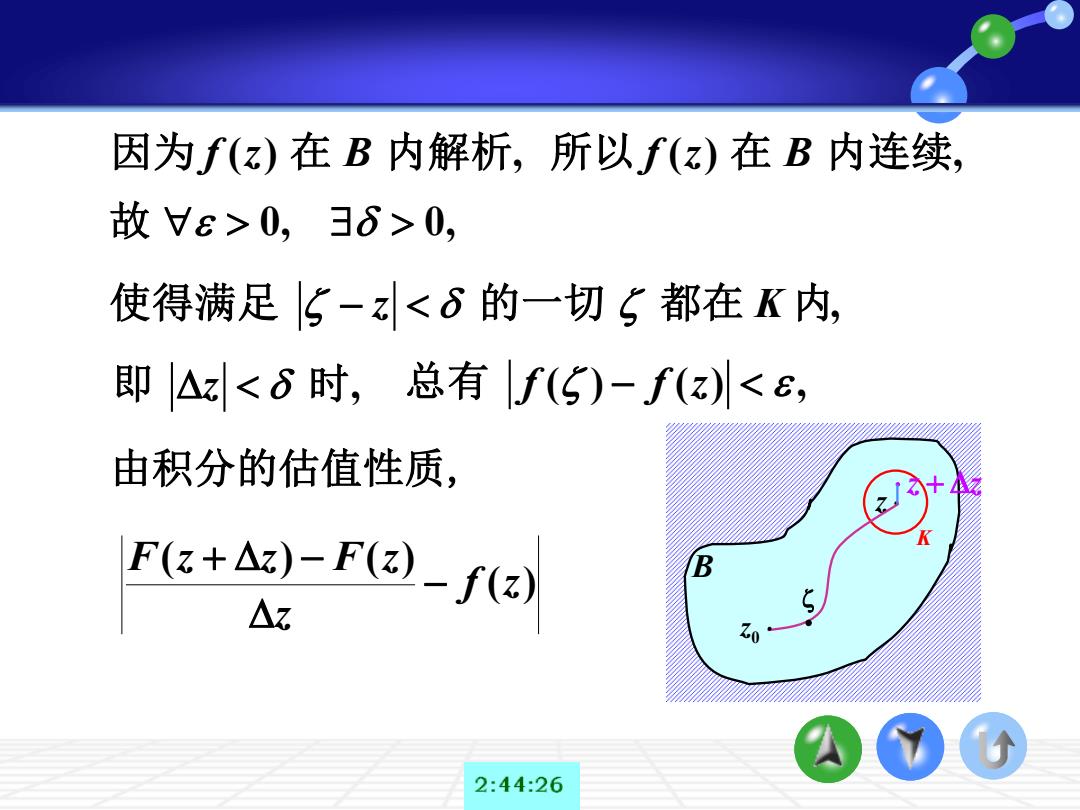
因为f(z)在B内解析,所以f(z)在B内连续, 故He>0,6>0, 使得满足5-z<6的一切5都在K内, 即△z<6时,总有f(5)-f(z<e, 由积分的估值性质, F(A)-F(-(Y B △z 2:44:26
B z K z + z 0 z • 因为 ( ) , f z B 在 内解析 所以 ( ) , f z B 在 内连续 故 0, 0, 使得满足 , − z K 的一切 都在 内 即 , z 时 总有 ( ) ( ) , f f z − 由积分的估值性质, ( ) ( ) ( ) f z z F z z F z − + −

Ee+a如-a-eF应*60-aa5 △z k起上fg-faus如6ac=s 于是 lim △z→0 Fz+)-F@-fe=0, △z 即F(z)=f(z). [证毕] 此定理与微积分学中的对变上限积分的求导 定理完全类似 2:44:26
( ) ( ) ( ) f z z F z z F z − + − [ ( ) ( )]d 1 f f z z z z z − = + | ( ) ( )| d 1 f f z z z z z − + . 1 = z z 0 ( ) ( ) lim ( ) 0, z F z z F z f z → z + − − = 于是 即 ( ) ( ). F z f z = 此定理与微积分学中的对变上限积分的求导 定理完全类似. [证毕]

2.原函数的定义: 如果函数p(z)在区域B内的导数为f(z), 即p'(z)=f(z),那末称p(z)为f(z)在区域B内 的原函数 显然F(a)=∫f(5)d5是f(z)的一个原函数. 原函数之间的关系: f(z)的任何两个原函数相差一个常数 证设G(z)和H(z)是f(z)的任何两个原函数 2:44:26
2. 原函数的定义: ( ) ( ), ( ) ( ), ( ) ( ) . z B f z z f z z f z B = 如果函数 在区域 内的导数为 即 那末称 为 在区域 内 的原函数 0 ( ) ( )d ( ) . z z F z f f z = 显然 是 的一个原函数 原函数之间的关系: f z( ) . 的任何两个原函数相差一个常数 证 设 ( ) ( ) ( ) , G z H z f z 和 是 的任何两个原函数

那末[G(z)-H(z]=G(z)-H'(z) =f(z)-f(z)≡0 于是G(z)-H(z)=c.(c为任意常数) [证毕] 根据以上讨论可知: 如果f(z)在区域B内有一个原函数F(z), 那末它就有无穷多个原函数, 一般表达式为F(z)+c(c为任意常数) 2:44:26
( ) ( ) ( ) ( ) G z H z G z H z 那末 − = − = f (z) − f (z) 0 于是 ( ) ( ) . G z H z c − = ( ) c 为任意常数 如果 ( ) ( ), f z B F z 在区域 内有一个原函数 那末它就有无穷多个原函数, 一般表达式为F z c c ( ) ( ). + 为任意常数 根据以上讨论可知: [证毕]

3.不定积分的定义: 称f(z)的原函数的一般表达式F(z)+c (c为任意常数)为f(z)的不定积分,记作 ∫fz)dz=F(a)+e. 定理三 (类似于牛顿-莱布尼兹公式) 如果函数f(z)在单连通域B内处处解析, G(z)为f(z)的一个原函数,那末 ∫fz)dz=G(z)-G(z) 这里z0,乙,为域B内的两点. 2:44:26
3. 不定积分的定义: ( ) ( ) ( ) ( ) , ( )d ( ) . f z F z c c f z f z z F z c + = + 称 的原函数的一般表达式 为任意常数 为 的不定积分 记作 定理三 1 0 1 0 0 1 ( ) , ( ) ( ) , ( )d ( ) ( ) , . z z f z B G z f z f z z G z G z z z B = − 如果函数 在单连通域 内处处解析 为 的一个原函数 那末 这里 为域 内的两点 (类似于牛顿-莱布尼兹公式)