
D0I:10.16355/j.cnki.issh1007-9432tyut.1988.02.013 第19卷第2期 Vo1.19恤.2 1988年6月 太原业大学学报 Jum.1988 JOURNAL OF TAIYUAN UNIVERSITY OF TECHNOLOGY 线性复数边界元的应用 许篱中 张淑芳 (数学力学系) 〔要〕本文对复数边界草元洪的基及其游,点作了探计,並推导了采用线 性元时的全部公式。为了改蒸方程组的稳定社,狩文献〔3〕中所用的柯西型积分 公式,改为奇异积分方程。 关键词:平面问题;边界元;数位方法 1引 言 随着实数边界单元法的不断发展,近儿华出现了复数边界单元法,Hutc11别 Hromadka,3]等人用复敩边界元法(GVB它M)求解拉普拉新方程,解决了流体力 学的勢流问题,文献〔4〕提出了解决弹性力学平面问题的复数边界元法。但文中采用 常数元,因而只能解几何形状剂受力情况很简单韵圆城问题。本文在文献〔4)的基础 上,采用线性复数边界元,并且为了改善稳定性,计算中采用的柯西型积分公式(第一 类Fredho]m积分方程)改为柯西积分的边界值公式(第二类F redholm积分方程)。按 导出的公式编出了程序,并纷出了鲸例。 复数边界元法不仅具育实数边界单元法的优点,如降低维数,城”计算机内存需要 量,计算精度高等,而且程疗编制比狡简单,最后得到的方程组的数阵比较稀疏,又 不依赖于所求问题是否有基本奇异解,因此是一种值得进一步摆讨剂发展的方法。 2复数边界单元法 弹性力学平面问题,可以袋变为下述复变厨数的边界值问题,即在边界为S的被研 究域D上寻求两个解析函数@,(Z):(Z)满足边界奈件: m,()+g()+,(0=i∫(x+Y)ds+s (1) 其中,X和Y为已知边界面力分量,积分是由边界上任选的基点1积到t点,Y:为待定复 本文1987年7月4日收到。 ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
9 第 卷 第 期 2 1 一去 一 或葺 f l 2 、 、 洲扮翎 、 ` ~ 忿洲 ` V o 1 . 9 酗 1 . 2 6 9 年 月 业 大 宇 学 报 8 81 J n u . 9 8 81 V E L T I 丁 工O O 工 N N N R R S A A A Y U U U F ’ H E C L T T O O O N G Y Y F 线 性 复 数 边 界 元 的 应 用 许菊中 张淑芳 ( 数学力 学 系 ) 〔摘要 〕 本 文 对 复数 边 界 单 元 法 的 基 仙 及 其特 点 作 了探讨 , 韭推 导 了采 用 线 性 元 时 的 全 部 公 式 。 为 了改 善方 程 组 的稳 定牲 , 将 文 献 〔 3 〕 中所 用 的柯 西 型积 分 公式 , 改 为奇异 积 分 方 程 。 关键 词 : 平 面 问 题 ; 边界 元 ; 数 值 方 法 引 言 随 着实 数边界 单元 法 的不断发 展 , 近 几年 出现 了 复 数边界 单元 法 , 壬玩n 科 , 丁 和 H : 。 m a 益 a 〔 ” 3 〕等人 用复 数边界元 法 ( C V 获三M ) 求解 拉普拉斯 方程 , 解决 了流 体 力 学 的势 流 问题 , 文 献 〔 4 〕 提 出 了解决 弹性 力学平 面 问题 的复数 边界元 法 。 但 文 中采用 常数 元 , 因而 只能解几何形状 和受力 情况 很简单 的 圆域 问题 。 本 文在文 献 ( 4 〕 的基 础 上 , 采 用 线性复 数边界 元 , 并 且为 了 改菩 虑定性 , 计 算 中采 用 的柯 西型积 分 公式 ( 第一 类 F : e 肚 。 ln 积 分方 程 ) 改为柯 西积分 的边 界值 公式 ( 第 二类 F r e 益 。 Jm 积 分方 程 ) 。 按 导 出的公式 编 出了程序 , 并 给 出了算例 。 复 数边界 元法 不 仅具有实 数边界单 元法 的 优点 , 如降低维数 , 减 少 计算机 内存 需要 量 , 计 算精度 高等 , 而且程片 编 制 比较 简单 , 最后 得到 的方 程组 的东数 阵 比较稀疏 , 又 … 不 依赖 于所 求问题 是 否有基 本 奇异解 , 因 此是 一种值得进一 步探 讨和发 展 的方法 。 2 复数边 界单元 法 弹性力学平 面 间题 , 可 以转变为 下沙 复变函数 的边界值 间题 , 即在 边界 为 ` 的被研 究 域 D 上寻 求两个 解析函数卿 , ( Z ) 和 必 , ( Z ) 满足 边界条 件 : : 1 ( , ) + : : ; ( : ) + 叻 , ( : ) 一 ` 丁} 。 ( 呀+ `万 ) 瑟: + : 名 , , 。 , ( 1 ) 其 中 , X 和 了为 已 知边 界面力 分量 , 积分 是 由边界上 任 选 的基 点 , 。积到 : 点 , 件 为待定复 本 文 1 9 8 7 年 7 月 4 日: }文到 。 DOI: 10. 16355 /j . cnki . issn1007 -9432tyut . 1988. 02. 013

90 太原工典大学学浪 19389 常滋,对于地速通域可取为容。注个问趣电可识解为这边界S上钓画数9,(t) ,(),使它满足方深(1),并分别作:D可谣所,在D5上连铁的函数:()剂 (:(Z)的边界值。根器复变函般理花可维,后者册充》必条件是 2j :(t) Z∈D (2) 其中D为边界S外的区域。方(2)是-类心.o,积分方程,腐散化为代数方 程组容易形减病念方程组,为此改捐刺西空积分进界值公式:【 iw(t)(1) = ()dt, 1-io t∈s (3) iw4o.()=∫. (1)d, ⊙(t。)表示1点处边界切线的 内角(图1),在光滑边界处, o(t。)=π。方程(3)是第二类 Fredholm奇异积分方程,右边的 积分应在柯西主值意义下求值。 现在的问题是首先要由微公 积分方程组(1)(3)求得S 上函数1(1)和4:()对此 ☒ 可以果带边界单元找示茶解。 (a) (b) 在离撤方程(1),(3)时,对了(3)心中成两个方强闪能分别在一边点上建 立。考虑到(2)(2)辩定览,以岩笼菜点的印:(!)(或中(公))科 1服中()值,并去掉指应点的方(3)河散式。求出边上9(1)和中:(1) 的值后,再按柯西积分公式进行数值计综杂得D内2点诗(Z),”(Z)和 1(Z) g (Z) ∫.2 91(1) (4) (2)=1. ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
太 旅 上 学 报 蕊鑫片肥妹 赢介井器抓分几盆宏粼华 ; _ 探 对 尸 使 的边界值 。 很粼复变函 如脚护犷知 , 后者 , 卜充分必 妥 条 件是 口 , 二 , 欺仕沁Z 常叭弘 ` 叭Z 任 刀ǐ `JI 洲 / 2 万 艺 丁 叭 ( 艺 亡一 公 ( 2 ) , 一 牲 广`I J 笼月卜 其 中一为 达界 , 外 叩且域 · 程组 容易子莎成病态方程组 , 方程 ( 2 ) 是第 一 关 曰 c lo il} 积 分 方程 · 离傲化为代 数 方 为此 改用村 西 拼积分边界 低公式 : 已 j 饭. ( 孟。 ) 甲, 扭 办 甲代约 才一 与 (l t , IJ 户. 、 勿 。, 。 ) 沪 , ( 公比 ) 一 _ 丁 ( 吕 ) 八U 任 S J … 、 … 叭 (t ) : 才一 去。 J 朽 认、 、 g 广 以刀 环协火 砂臼砂介示 朴点处边界切 线 的 犷可以步御有边界单元技术不解 。 州 口 。 、 、 、 图 1 交“ ) ( 乙 夕 在离欲方崔 ( 立 。 考虑到 甲 士 ) , ( 吕 ) 时 , 对于 _ ( 名 ) 式中 的两 个方程 只需分 红` ) 补八 名 ) 、 协谕定 砚狡 , 六儿 明 以)值 , 并 去 掉椒 应点的方 江 t 3 _ 川厂扮定 从点妙叮 公 的离散式 。 求 出边梦舀 _ 七 别在一 二笋边界点 一七建 ) ( 成 如 ( 么 ) _ ) 和 叭 ( 公 ) 和 劝 士 ( , ) 笠忠卿畔卿严淞畔妙 力次叮 ’ 冲 1 份 华 夕 (幼 和 叭 〔约 ( 一 去一 名 ) “ 、 门励 一咨 一 f 无 乞 J 万 ( 4 ) 、 i 卜 | 卜 ; | J Jse 广l| 沪, . r 币ù么流l ` 以ù é 改 刁 澎 、 , : ( : ) 一 _ : _ _ r 公万 才 J “ , 二 、 工 f 气。 少 - 一 ; I 2汀 容 J , 内 ( 约 以一 z )

第2阿 许京中线性红致边界元的应用 91 最后可得Z点的应力 o:=Re〔2φ{(Z)-Zp”(Z)-(Z)〕 0,=Rc〔2(Z)+Z9“(Z)+0;(2)〕 (5) Ty=1〔Z9:(Z)+(2)〕 3线性复数元的应用 如果将边界S剂分为段,毁的端点(称结点)记为t,t,+,用连结两端点的直线 近似宾实的边界,并记为△,。月线性函数 时(1)=9,a》+9(+)二9:2(-1,) (6) 荆 1i+1-f: (a)=:(t》+()二2(a-t) (7) i+1-: 近似实际的待求函效。如果在诗=)点建立方程(1),可得 2 p.(1,)+g)++1.9(t+)一9()+ 2 2 i-1i +1D+(+1D=B,. (8) 其中 x+亚)ds (9) 对x点列出方!(8)中第-…式为 p}(t) io)m,x)=∫ 9,()1=2 ΓL-tx i h. (10) 对不含的各段,将式(6)代入积分式可得 2+(小o -【+1()].) (11) ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 明 2 许翁 中 线 性复数边界元 的应用 9 1 Z 最 后可 得 点 的应 力 J : 一 五 。 〔 拭 2 叮 、 一 脚 〔 侧 2 j Z 一 甲夕 ) ( Z Z 十 甲 尸 ) ( Z 拭 ) ( Z 拭 ) +( 5 ) 丁二 。 J Z Z Z 一 川 〔 分 侧 〕 ) ) ( ( + ( Z 〕 ) ) ( Z 〕 ) { } 尹 线性复数元 的应用 3 如果 将边界 叮剖分为 : 段 , 万段 的端点 ( 称 结点 ) 记为 才, 和 t , l 一 : , 用 连 结两端点 的直线 近似 真实 的边 界 , 并 记 为△ : , 。 厂j线性 函 数 卿 { ( 艺) ( 6 ) 和 一 甲1 ( 艺了 ) 十 哭 一 汾乍汽必之( ` 一 , , 喇 (幼 一 动 , ( 耘 ) + 州粉胃 丛丝 ( ` 一 ` 了 ’ ( 7 ) 近 似实 际 的待求函数 。 如果 在 群 ( z 夕 + 艺 2 】 互点建 立方程 ( 1 ) , 可得 处 匕片竺恤 上迫 一 十 才 + 才 2 甲 , ( 幻 。 一 ) 一 十 艺7 一 卜 守: , ( 才 ) 才了 , 不 一 万牙万 一卜 丽(不门了 一 I一 — - — 一一 - 一 一 一丁 一一一 — - 一一一 艺 = 刀 ( 8 ) 其 中 刀 一 : { 才尤 ) ’ (呀任 一 `歹 一 ) / ` ( 9 ) 对 : 二 傲列 出 方程 ( 吕 ) 中第一 式为 甲 」 (户 内 t 一 才` 列 、 ( 约 — 一 J 公 才一 公兀 ( 1 0 ) 下 盛 土J 护 , . J卜子才 内 l we , : 。 ( ; 二 ) : ( , · ) 一 { 仓 对不含 : ; 的各段 , 将式 ( 6 ) 代 入积分 式可 得 才矛+ i 一 t 天 t i 一 t 万 一 )〕 甲 工 ( ` , · ` , - 了、.、 / n 1 上 { 云 z+ 工 甲 { ( t ) t 一 才兀 、 , 一 1 1 十 艺x 一 t , 才了+ , 一 才z . 、`Z `r 了户、 甲 ,J.` ` 、尹刀, 亡尺一 一一代 + ù 7 声叭矛、 上二 (竺兰 1n t 十 工 一 如 ( 正1 了+ ) .rL 一

92 太原工业大学学拔 198路门 而注人一1和K两段上积分是奇异积分,按积分柯西主值计算 9-(t) -1二1x + -1 p:(1) A+ =p.-9-)+p.1[二经] (12) 将式(11)和(12)代入(10)可得 e+【1m:授-i01])-9.+ +{[+(g-)门 【1+()门)}=0 (13) 对中(t)也有类似方程。如在所有边界点建立方:(8),对9,(1)府中:(1)分别在一半 边界点建立方程(13),分开实部和虚部,并在给定p:和1m,的点处去掉相应的方程, 可得求解n个边界节点上的p,和中:值的方程组。求得中:和中,的边界节点值后,果要求域 内某一点Z的应力分量;仍然可采用分段数值积分求P:和中的导数,这时Z是D域内的点, 所以 -z):h =22{(222)(9.0+ +二子.)+以1(7)》(1) 财网-小a= =之{(4,22-是2)× ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
自 太 原 工 2 之 大 学 学 报 j 而在兀 一 」和 两段 上积分 是 奇异 积分 K , 按积 分 的柯 西主 值计 算 { 才K ( t ) Z 人 (了介 一 ’ (公 `r . ) re lL 」恤 兀、 一 . ō 口了 : ` Z ~ 1 。 工1 口 才+ t 兀 _ 1 一 t K “ / 十 { ;; 衬 ( 约 石 一 Z` 去` 一 z 飞一 才犬 甲杏 ( , ) _ _ 一 — d 去 t 一 才入 〕 一 、 , ( , · + , ) 一 : , ( , 一 ) + 。 : ( , · ) : · l £ 卜 才入 十 一 才 K Z 扳 _ 1 一 t 入 } 将式 ( 1 ) 和 ( 12 ) 代入 ( 10 ) 可 得 、 1 ( 才一 ) 、 一 【 ` 1飞 生 . 一 : 的 (艺、 ) K { 叨 : ( z 、 ) 一 卿 1 ( 艺,、 一 l ) 一 卜 才 +t 一 艺K 岛 一 t 尤 ) } 中工 ( ` , · ’ ) - 了`、r 抽一 九 八 衍一 ù J 十 坏 、r .L .rIL 陀白刘冲 + t K 一 jt 刊 艺j + : 一 才, 艺入 才万一 公兀 )] 叭 ( `呀 一 。 ( 1 3 + 叹 ) 咭土 r .L 一 对 动 , ( i) 也有类 似 方程 。 如 在所有 边界点建 立 方程 ( 8 ) , 对 卿 , ( , ) 和妙 , 以 ) 分别 在一 半 边界 点建 立 方程 ( 邓 ), 分开 实 音盯: J虚部 , 并 之给定 甲 , 和 I 瑕 cj) , 的点处 去 掉相 应的方程 , 可 得 求解 二 个边 界节点上 的卿 和 必 1值 的方程组 。 求得 ( 、 、和 叻 的边界 节点值 后 , 如果要求域 内某一 点Z 的应力分量 ; 仍 然可 采用 分 段数值积 分求叭 和 叭 的导 数 , 这 时Z 是 D 域 内的 点 , 所以 , 甲 { ( z ) 一 又万匀 2 心 亡J 了了F 月 l .. J ) ( 下架补 , , 夕+ 1 ` ] 甲 , ( 才, 卜 , 一 ) 十 侧 (Z ) 二 间一艺 1 2兀 Z 六 二 1 2兀 Z 约)Z 创-(t 广」飞 1 之 , f , 1 = 二花下 . 二 一 乙 万 气 一丁一 7 - Z兀 2 , 二 1 ` 、 ` 一 万 一 ` 1 一 Z + 才, 干 , t 厂1 1 一 Z 二 t丁甲 ` 戈乙` ’ ) 十 一少耳 才川二式 一 二旦 : · ( 公 、 , 一 Z t , 一 Z ) } · ( 」4 ’ 卫岁公护. . 杯 ? 丫例封 华了 (Z ) 卿 , ( t ) ( 才一 Z ) “ d t 二 1 兀 2 才 华 { ( 才) (不盯 3 六 又 、、仁 下 严矛 ǔ 1 ( t ; 一 Z ) “ 口 , 、 , 一 Z ) " 内叫 . ,1 艺钊 万
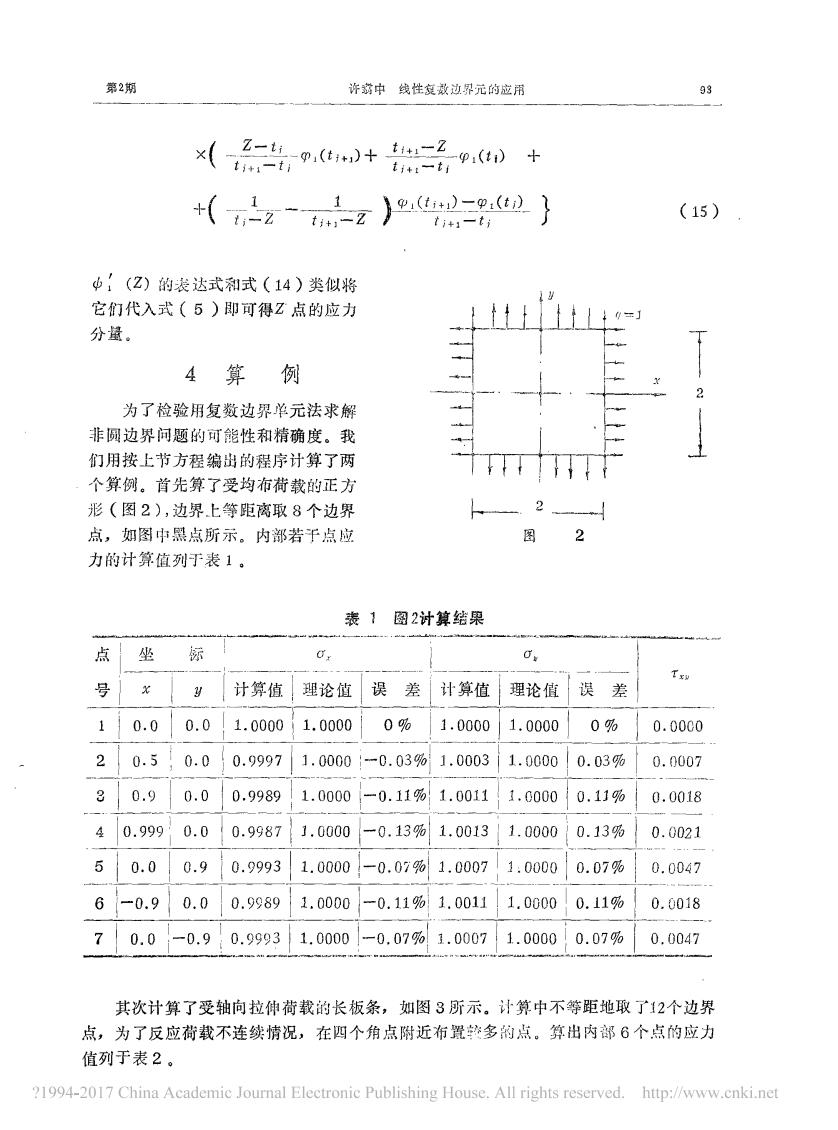
第2期 许游中线性复数边界元的应用 93 (+二号 t-克p(0大 +(z-z)} (15) tit-ti 中!(Z)的装达式和式(14)类似将 它们代入式(5)即可得Z点的应力 分量。 4算 例 为了检验用复数边界单元法求解 非圆边界问题的可能性和精确度。我 们用按上节方程编出的程序计算了两 个算例。首先算了受均布荷载的正方 形(图2),边界上等距离取8个边界 点,如图中黑点所示。内都若子点应 力的计算值列于表1。 表1图2计算结果 点 坐 标 Ux 0 Tx型 号 y 计算值 理论值 误 差 计算值 理论值 误 差 1 0.0 0.0 1.0000 1.0000 0% 1.0000 1.0000 0% 0.0000 2 0.5 0.0 0.9997 1.0000 -0.03% 1.0003 1.0000 0.03% 0.0007 2 0.9 0.0 0.9989 1.0000 一0.11% 1.0011 1.0000 0.11% 0.0018 4 0.999 0.0 0.9987 1.0000 -0.13% 1.0013 1.0000 0.13% 0.0021 5 0.0 0.9 0.9993 1.0000 -0.07% 1.0007 1.0000 0.07% 0.0047 6 -0.9 0.0 0.9989 1.0000 -0.11% 1.0011 1.0000 0.11% 0.0018 7 0.0 -0.9 0.9993 1.0000 -0.07% 1.0007 1.0000 0.07% 0.0047 其次计算了受轴向拉伸荷载的长板条,如图3所示。计算中不等距地取了12个边界 点,为了反应荷载不连续情况,在四个角点附近布置整多的点。算出内部6个点的应力 值列于表2。 ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 期 许翁中 线性复数 边界元 的 应 用 2 一 幻 Z t s 一 卜 , 一 t i 砂 , ( 公 , , , ) + ` 1+ 1 名 J t 护+ z 一 t i 华 , ( 才, ) + 工 尹、皿一, t 挤* 1一 Z , ( t , 干 , ) 一中 , ( t , ) t , + , 一 t , } ( 1 5 z一 一 ) 一1一 `尾了、 `了桂、 +X 丁| ` 才2 t l 日斗 生 l 可斗 功: (Z ) 的表 达式和式 ( 14 ) 类似 将 它们 代入式 ( 5 ) 即可 得 Z 点 的应 力 分 量 。 4 算 例 为 了检 验用复数边 界单元法 求解 非 圆 边界 问题 的可能 性和精确度 。 我 们 用按 上节 方程 编出 的程序 计 算 了两 个 算例 。 首先 算了受均布荷载的正 方 形 ( 图 2 ) , 边界 上 等距 离取 8 个边界 点 , 如 图 中黑点所 示 。 内都 若干 点 应 力的计 算值 列于 表 1 。 2 图 2 表 霭 图 2计算结果 计算值 1 . 0 0 0 0 理论 1 . 0 0 0 0 1 0 % 0 . 0 0 0 0 2 … 。 · : { 。 · 。 …。 · 9 9 9 7 1 」 · 。。。。 一。 · 。 3 、 … 」 · 。 。。3 … , · 。。。。 ` 。 . 0 3 * … 。 . 、。。。 7 了} 一 d二 一 … 一 百万 一 …而茄… 一丁 一 石丽 一 {二石玉碱 一 五茄五 一 } 一 至 一 。。。 。 { 。 . 1 ,厢 一 … 一。一丽万 一 4 … 。 . 9 9。 , 。 . 。 …。 . 9 9 8 : … 」 . 。。。 o …一 。 . , 3肠 … , . 。。 , 3 } , . 。。。。 」 。 . , 3肠 } 。 . 。、 , 5 … o · “ } 。 · ” … 。 · 9 9 9 3 } l · 。 0 0 0 }一 0 · 0 7物 … 1 · 。 0 0 7 … 生 · 。 0 0 0 …。 · 。 7% … 。 · 。 O` 夕 石 一 … 一 0 . 9 { 。 . 。 … 。 . 9:云… , . 。。 。。 … 一 。 . 1 1司 一王万丽} 一 ;石而 ! 。 . 1 1* … 一 石 一 。云 1言 一 7 … 。 . 。 { 一。 . 9 { 。 . 9 9 9 3 } 1 , 。。。。 ,一 。 , 。 7 * … , . 。。 。 7 … 1 . 。。。。 … 。 . 0 7* { 。 . 。 。; 7 其次计 算了受轴向拉伸荷载 的长板 条 , 如图 3 所 示 。 计 算 中不 等距 地取 了提个 边界 点 , 为 了反 应荷载不连续情况 , 在 四个角点 附近 布置 朴多 的点 。 算 出内部 6 个点 的应力 值列于表 2
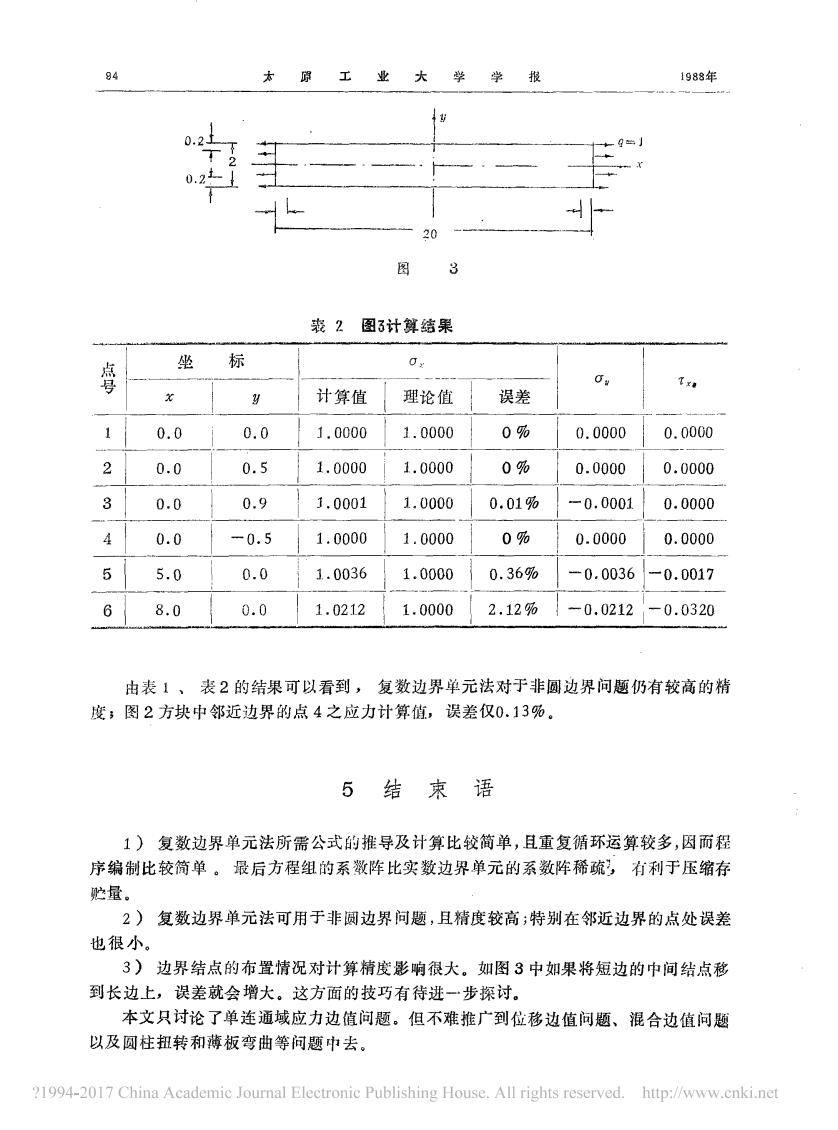
94 本原工业大学学报 1988年 0.2 图 3 我2图3计算结果 坐 标 喜 Txa y 计算值 理论值 误差 0.0 0.0 1.0000 1.0000 0% 0.0000 0.0000 2 0.0 0.5 1.0000 1.0000 0% 0.0000 0.0000 3 0.0 0.9 1.0001 1.0000 0.01% -0.0001 0.0000 4 0.0 -0.5 1.0000 1.0000 0% 0.0000 0.0000 5 5.0 0.0 1.0036 1.0000 0.36% -0.0036 -0.0017 6 8.0 0.0 1.0212 1.0000 2.12% -0.0212 -0.0320 由表1、表2的结果可以看到,复数边界单元法对于非圆边界问题仍有较高的精 度;图2方块中邻近边界的点4之应力计算值,误差仅0.13%。 5 结束语 1)复数边界单元法所需公式的推导及计算比较简单,且重复循环运算较多,因而程 序编制比较简单。最后方程组的系数阵比实数边界单元的系数阵稀疏,有利于压缩存 贮量。 2)复数边界单元法可用于非圆边界问题,且精度较高;特别在邻近边界的点处误差 也很小。 3)边界结点的布置情况对计算精度影响很大。如图3中如果将短边的中间结点移 到长边上,误差就会增大。这方面的技巧有待进一步探讨。 本文只讨论了单连通域应力边值问题。但不难推广到位移边值问题、混合边值问题 以及圆柱扭转和薄板弯曲等问题中去。 ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
4 5 9 方 原 工 业 大 学 学 报 玉9 年 8 斗 - - 一 一 舟 · 一 一 T . Zw e HW守 勺` , ù Z 图 吕 表 2 图 3计算结 果 号点 0 . 0 0 . 0 理论 值 」 . 0 0 0 0 0 . 0 0 0 0 0 . 0 0 0 0 0 . 0 0 , 0 0 。 0 5 . 0 } { 一 { 0 . 弓 计算 值 1 . 0 0 0 0 1 . 0 0 0 0 J . 0 0 0 1 1 . 0 0 0 0 」 _ . 0 0 3 6 1 . 0 2 12 .1 0 0 0 0 误差 O 肠 O 呱 0 . 0 0 0 D 0 . 0 0 0 0 0 . 9 1 , 0 0 0 0 0 . 0 1 肠 一 0 . 0 0 0 1 0 . 0 0 0 0 一 0 . 5 1 、 0 00 0 O 肠 0 . 0 0 0 0 } 0 . D0 O0 ! l 一、… 二 :| , … 0 . 0 1 ` 0 0 0 0 0 , 3 6 肠 一 0 . 0 0 3 6 {一 0 . 0 0 1 7 8 . 0 0 . 0 1 . QOOO 2 . 拐 肠 } 一 0 . 0 2 12 一 0 . 0 3 2 0 二止 由表 1 、 表 2 的 结果 可 以看 到 , 复数边界单 元法对于 非 圆边界 问题仍有较高的 精 度 ; 图 2 方块中邻近 边界 的 点 4 之 应 力计 算值 , 误差 仅。 。 1 3肠 。 5 结 束 语 l) 复数边界 单元法所需 公式 的推导及计算比较简单 , 且 重 复循 环运 算较多 , 因 而程 序 编制比较 简单 。 最后 方程组 的系数阵 比实 数边 界单 元的系 数阵 稀疏 , , 有利 于压缩存 贮量 。 约 复数边界 单元法 可用 于非 圆边界何题 , 且 精度较高 ; 特 别在 邻近边界 的点 处误差 也 很 小 。 3 ) 边 界 结点 的布置情 况对计算精度 影响很大 。 如图 3 中如果 将 短 边的 中间 结点移 到长 边 _匕 误差就会 增大 。 这方面 的技巧有 待进一 步 探讨 。 本文 只 讨论 了单连 通域应 力边值间题 夕 但不难 推广到位移 边值问题 、 混 合边值 问题 以及圆柱扭转和 薄板 弯曲等何题 中去

第2期 许教中线性复数边界元的应用 95 参考文献 1 Hunt B,Isaacs L.Integral equation formulation for ground-water f1ow.J.Hyd.Div.A.S.C.E.1981,107(HY110):1197~1209 2 Hromadka T V,Guymon G L.A complex variable boundary element method:develonment,Int.J.Nnmer.Method Eng.1984,20:25~37 3 Hromadka T V,Yen CC,Guymon G L.The complex va rable boun- dary element me thod:Applications,Int.J.Numer.Mcthod Eng. 1985,21:1013~1025 4许翥中,许捷,弹性力学平面问题的复数值方法.太原工业大学学报,1986, 4:39~44 5赵桢.奇异积分方程.北京师范大学出版社,1984:129~130 6赖汉卿.复变数函数论.台北:徐氏基金会出版,1978:57~58 米米米 米米米 米米米 AN APPLICATION OF LINEAR COMPLEX VARIABLE BOUNDARY ELEMENT Xu Zhuzhong Zhang Shufang Abstract) The basis of a complex va riable bounda ry element meihod for the plane problems of elasticity is discussed in this paper and formula- tions for linear CV BE are given.The singular integral equation is used to provide stable solutions. Key words:plane problems;bounda ry element;nume rical method ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 期 许素2 中 线 性复数 边界元 的 应 用 9 5 H u n t l f o w 参 B , 1 s a a e s L . I n 飞e g r a 考 文 献 . J . H y d . D iv . A . S . C . 1 e q u a t i E . 19 8 1 , o n f o r m u l a t i o n 1 0 7 ( H Y i 1 0 ) : f o r g r o u n d一w a t e r J J 9 7 ~ 」2 09 2 3 4 H r o m a d k a T V , G u y m o n G L . A e o m p l e x v o r i a b l e b o u n d a r y e ! e : n e n t m e t h o d : 乙。 v e l o n m e n t , I n t . J . N n m e r . M e t h o d E n g . 19 8 4 , 2 0 : 2 5 ~ 3 7 H r o m o d k a T V , Y e n C C , G u y m o n G L . T h e e o m p l e x v a : 。 b l e b o u n 一 d a r y e l e m e n t m e t h o d : A卫 p l i e a t i o n s , 玩 t . I . N u rn e r . M o t h o d E n g . 19 8 5 , 2 1 : 1 0 13 ~ 1 0 2 5 许 蠢中 , 许捷 , 弹性 力学平面 问题 的复 数值 方法 . 太原 工业 大学 学报 , 1 9 8 6, 4 : 3 9~ 4 4 赵祯 . 奇异积 分 方程 . 可氏 师 范大 学 出版社 , 19 8 4 : : 2 9 一 」30 赖汉卿 . 复变 数函数论 . 台北 : 徐 氏基 金会 出版 , 」 一 9 7 8 : 5 7 ~ 义 56 今各米米 来来来 带余米 A N A P P L I C A T IO N O F L I N E A R C O M P L E X V A 尺I A B L E B O U N D A R Y E L E M E N T X u Z h uz h o n g Z h a n g S h u f a n g ( A b 0 t r a e , ) T h e b a s i s o f a e o m p l e x v a r i a b l e b o u n d a r y e l e m e n t nt e t h o d p l a n e p r o b l e m o o f e l a s t i e i t y 1 5 d i s e u s s e d i n t h i s p a p e r t i o n s f o r l i n e a r C V B E a r e g i v e n . T h e s i n g u l a r i n t e g r a l , a n d e q u a t i f o r 1 l l e f 0 r m u l 及一 o n 1 5 屯2 5 e d t o P r 0 V J K e y d e s t a b l e 5 0 〕 u t i o n s w o r d s : p l a n e p r o b l e m s ; b o u n d a : y e l c m e ,: 士; n u m e r i e a l m e t h o d