
第22卷第2期 力学学报 Vol.22.No.2 1990年3月 ACTA MECHANICA SINICA Mar.,1990 夹层板的复变边界元解法 质镭 黄茂光 (中国科学技术大学近代力学系) 提要本文用全纯函数表示微分方程△(x,y)一(+,y)■0的一般解,粮据全纯函 ,:数的Bky积分表示法,建立了复数域内的边界积分方程并针对各种边界条件下Ri- ner)型夹层板、Hoff1型夹层板进行了数值求解。 关键词边界元法、夹层板。 引言· 复变边界元法近年来在数值求解调和方程边值问题方面发展较快4),其主要思想是 把偏微分方程的一般正则解用全纯函数表出,根据问题的边值条件用柯西积分公式建立 边界积分方积并用边界元离散求解。由于柯西公式导出的积分方程中未知函数是边界上 的复函数,因此往往需要增加某些定解条件或采用一些数学技巧,化去某些未知量方能求 解。 本文首先导出微分方程△(x,y)一1(x,y)▣0在复数域内的一般解,然后用 Bekya全纯函数积分表示法建立了各项同性夹层板(Reissner型与Hoff型)在任意边 界条件下的积分方程。采用本文方法导出的积分方程中未知函数仅是边界上的实函数, 因此不器要增加定解条件就可用边界元法进行数值求解, 一、用全纯函数表示夹层板方程的一般解 胡海昌把Reissner型夹层板的基本方程归结为求解两个函数F(x,y)及f(x,y) 满足方程: D△2F(x,y)=g(x,y) (1) D(1-)△,y)-cs,y》=0(x,)e② (2) 2 在边界条件: w=而,中。m中.,中,=山,(*,y)∈0 (3) 知=m,M.=a.,中,=中,(x,y)∈O到, (4) M,=M,M。=M,Q.=2。(x,y)Ea②, (5) 下的定解问题.其中:D—夹层板的抗弯刚度;C一夹层板的剪切刚度;一表, 层的泊松系数。 it. 本文于1989年1月18日收到. ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 卷 第 2 期 2 l , , 。 年 J 月 力 学 学 报 A C T A M E C H A冲 C A sl N I C A V o l . 2 2 , N o . 2 M a r . , 1 , 9 0 夹 层板的 复 变边界元 _ 解 法 顾 镭 黄茂 光 (中国科学技术大学 近代 力学系 ) 提耍 本文 用全纯 函数表示微分方程 ` f ( 二 , 对 一 补 f ( : , 约 , 。 的一般解 , 根据全 纯 函 数的 eB k ya 积分表示法 〔 `川 , 建立了复数蜂内的边界积分方程并针对 各种边 界条件下 eK is - en 产 , 型夹层板 、 H o fr ” 型夹层板进行 了数值求解 . 关锐词 边界元法 、 夹层板 . 引 言 ’ 复 变边界 元法近 年来在 数值求解调和方程 边值问 题方面发展较快 .[ 一 ` , , 箕圭要思想 是 把偏微分方程的一般正则解 用全纯函数表出 , 根据问题的边值条件用柯西 积分公式建立 边 界积分方积并 用边界元离散求解 . 由于柯西公 式导 出的 积分方程中未知 函数 是边 界上 钓 复函数 , 因此 往往需要增 加某些定解 条件或采 用一些数学技巧、化去某些未知量方能 求 解 。 本文首 先导 出微分方程 。 f ( 二 , 力 一 巧 ( 二 , y ) 一 。 在 复数域内的一般解 , 然 后 用 eB k ay 全纯函数积分表示法建立了各项同性夹层板 ( R e is s ne r ` 型与 H of f 型 )在 任 意 边 界条件下的积分方程 . 采用本文方法导出的积分 方程中未 知函数仅 是边 界上的 实 函 数 , 因此 不需要增加定解条件就可用 边 界元法 进 行数值 求解 . 一 、 用全纯函数表示夹层板方程的一般解 胡海 昌切把 R ie s s en r 型夹层 板的基本方程归结 为求解两个函数 F ( x , 力 及 f ( : , 力 满足方程 : 、J ù 、叮 、护.矛 `几, , 、夕 D△ Z F ( x , y ) 一 宁( 二 , y ) 旦 ( l 一 , I )△ r( 二 , , ) ’ 一 e r( 二 , , ) 一 。 ( 二 , y ) 。 缈 2 在边界 条件: , ~ 而 , 巾 。 ~ 必 。 , 少 , ~ 必 , ( 二 , y ) 〔 刁日多: ( 3 ) , 一 而 , 衬 。 ~ 厨 . , 价 , ~ 价 , ( 二 , y ) 〔 a少 : ( 4 ) .M ~ 丽 , , M 。 ~ 厕 一 , Q一 口 . ( 二 , , ) 。 。`多 , ( 5 ) , 卞的定解 问题 . 其中: D — 夹层 板的抗弯刚度奋 c — 夹层板的 剪切 刚度 ; 约 — 表 , 层的泊松系数 . 、 ` · 一 本文于 l , 协, 年 1 月 l 公 日收到 -

164 力 学 学报 (1990年)第22卷 司1+C②,16四,一6功为域②的边界;0、b、中、M、M、。均为边界上的已知 函数,而w、中、中、M、M、.均可由F及f表出. 基本方程(1)一(2的解可由齐次通解与任一特解迭加而得,特解与荷载9(x:y)有 关,一般可直接求出,本文仅讨论齐次方程: △2F=0 (6) △f一5m0 (7) 的一般解。 方程(6)在复域的一般解为: F()=Re[xp()十p(x)】z=x+y∈现 (8) 其中m(),()均为现内的任意全纯函数,当m、p满足条件: p1(0)=p(0),p2(0)=p2(0) (9) 时,,p由F()唯一确定. 下面推导方程(7)的一般解。设(7)的一般解具有形式: f)-R(-军国+[e0(e)+en]R[-¥(1-)]:(1o 其中()为内的任意全纯函数,,为任意的实常数,R(X)为一待定函数. 把(10)代入)冲并注意到△1-4,有: A-好=-'[R(-翠)-R(-翠)+R(-a月 {--)[琴(1-+R(1= +R[-¥(1-)}[e(e)+(e)I (11) 令: 则(11)式可写成: △f-H=-a[5R()+R()+R(1-2产5R() +R(5)+R()}[(z)+zp(zt)] 如果我门选择的函数R(X)满足条件: XR"(X)+2(X)+(X)=0 (12) 则表达式(10)即为方程(7)的一般解. 令: L0-会-0品 (13) 容易验证1(X)满足条件(12),以L(X)代(10)中的R(X),则(7)的一般解可写成: fe-a(-¥)+2j。e0e1L-21-4 (14) ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
力 学 学 报 ( , , o 年 1 ) 第 珍 卷 口, ; + 己勿 , 、 一 。少 , 一 。必 为域 必 的边 界 ; 奋 、 必 , 、 小 : 、 丽 。 、 丽 , 、 奋 。 均为边 界上的 已 知 函数 , 而 留 、 必 . 、 沙 , 、 M 。 、 M , 、 Q 。 均 可由 F 及 f 表 出〔, , . 、 厂馨潺漏翼努篡翼馨严哪 加畔 {簿蜂是钾“ 卿 ’ “ 、`ZZ 产On 、、了尹 、 △ Z F 二二 0 八 2步一 几丫一 的一般解 . 方程 ( 6) 在复域的 一般解为 〔l] : F ( 幻 ~ R成 , 种 1 (幻 十 外 怡) 1 其中 甲: (幻 , 甲2 (幻 均 为必 内的任意 全纯函数 , 当 ( 6 ) ( 7 ) 言 ~ 二 十 iy e 勇 咖 、 补 满足条件 : 时 甲: ( o ) ~ 甲: ( o ) , 甲2 ( o ) ~ 中2 ( o ) 甲: , 中: 由 F ( , ) 唯一确 定 . 下面 推导 方程 ( 7) 的一般解 . 设 ( 7 )的一 般解具有形式 : `闭 一 a0 “ ( 一 分小 皿呵佃 , 十 厕叫 一 分和 一 。卜 …一 ( ` Q, 其中 《 幻 为必 内的任意全纯函数 , 。。 为任意的实常数 , R 汀) 为“ 待定函魏价专 一 把 l( 0) 代人到 ( 7 ) 中并注 意到 △厂一 4 洲 兔旅 有 、 一 。 一耐 2 阿 一 知) 一丁砂 , , ( 一 知) 十 “ (谓州 一 土 : 三( 1 一 约及 卜分i(l 一价 礼升子铆 种{ 上JIf ù l , . ù 一无 + : 卜 一 f · 牙( ` 一 , {} t · , (一 卜 牙, (一 , ,“ ( 1 1 ) 丫 — — 多之 ~ 乌 又 ` 一 / . 一 、 - 一 一 万 万 戈丈 一 勺 一 则 ( 1 1) 式可写 成: △ f 一 、 , 一 。 。 又2「; * , , ( ; ) 十 : , ( ; ) 十 * ( ; ) 1 一 : Z C {; * , · ( ; ) + 尺 ` ( 畜) + R ( 占) } 〔牙中( z t ) + z 公( : ` ) ] ,多t 如果我们 选择的 函数 R ( X ) 涛足 条件 : X 灵“ (尤 ) 十 招 ( 尤 ) 一卜 女( 厂 ) 一 。 则表达式 ( 10 )即为 方程 ( 7 )的一般解 , ( 1 2 ) 令 乙0( X ) 一 X 凌 丹卜 ` ’ ` 、扮 容 易验 证 乙。 ( X ) 满 足 条件 ( 12 ) , 以 L 。 ( X ) 代 ( 10 ) 巾 的 R ( X ) , 则 卿 ( ’ )的一放解句绮成{ f ( : ) 一 。 。 ; . ( 一 兰 : *卜 2 { ’ R e [ : 。 ( z ` ) ]: 。 \ 斗 1 J O 一 今 : 云l( 一 , ) 毛真 ` - - 卜 (l 4 )

第2期 顾镭等:夹层板的复变边界元解法 165 为便于以下积分方程的推导,命: m()-+( (15) 2 J。 上式中()仍为必中的全纯函数,且有: (0)=p(0) (16) 把(15)代人(14)中,可得: K)-2RelmRet(dr (17) 其中m()为②内任意的全纯函数,在满足条件(16)时()由()唯一确定。 二、边界积分方程的建立 可以证明:域现内任意的在边界8现上m阶可导的全纯函数中()均可表成 (Bekya): b()-∫n(+Ne,0+c …(18) , (,)-(1-)(1-)+1 其中a(+)是在边界a哑上满足H6lder条件的实函数,C为实常数,4(+)和C由 b(g)唯一确定。 根据(18)式,我们有: px()-J。4(+,,Db+CxK-l,2,3 (19) 总1(+),A2(+),A(+)为定义在②上的实函数;C、C、C为实常数,根据条件 (9)、(16)可知C:■C2一C,=0;m为一正整数,m的选取与边界条件有关,在夹层板 问题中m≥3,在本文以下的算例中我们取m=6(并不是必要的). 把(19)式代入到(8)和(17)中,可以写出: F(z)=LfA(+),A(+),z] (20) f(s)=L[A(+),2] (21) 其中L,L均为积分算子: Reds ,ds (1) L(a,)-2Ree4wds-a到65,☑ ×[-若a1-s4sasy (23) 由于边界条件(3)一(5)均可由F,f表出,把(20)、(21)代人进去,并令z→∈0吻,我· 们可得到以A(+),4,(+),A,(+)为未知函数的边界积分方程(见附录),简记为: Lwo(A1,42,A3,老)=00∈0☑, ) Lw(4,A,4,)=0.高∈0②, (25) ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 期 顾 钳等 : 夹层板的复变边界元解 法 为 便于以 下积分 方程的 推导 , 命 : , (幻 、 , + ( ’ 一 。 (。 * 2 夕 o ( 15 ) 上式中 咖 (幻 仍 为必中的全 纯函数 , 且 有 : 礴(的 ~ `斌可 把 ( 王5 ) 代人 ( 14 )中 , 可得 : , 。 , , 、 , 泛2 _ r l , , , 、 , , , f 几2 _ , . _ 、 1 . f ( 。 ) 一 Z R e [甲3 ( 二 ) ] 一二 : 牙 } R e [中, ( : ; ) ] L a } 一 乏 : 牙( l 一 , ) }由 2 ) c 一 L 4 一 J 其巾 . (幻 为粤内任意的 全纯函数 , 在 满足 条件( 比)时 甲, (的 ’ 由 f( 幻 唯 一确定 . ( 16 ) ( 1 7 ) 二 、 边界积分方程的 建立 j 可以证明切 : 域 必 内任意 的在 边界 。少 上 m 阶可导的全纯 函数 沙 (刃 均 可 表 成 ( B e k y a ) : * ( · ) 一 { 。 , , ( + ) 、 。 ( · , : ) * 一+ `e ( 18 ) N 。 ( 二 , , ) 一 ( 1 一 二、 ` 一` I n ( 1 一 、 ` 、 十 ; 、 多 , 、 , / 其中 试 + ) 是在 边界 跳勿 上 满足 ~ H七l d比 条件 的实函数 , c 为 实 常 数 , 夙 卞) 和 c 由 沙 (刃 唯一确定 . 根据 ( 1 5) 式 ,我们 有 : 月、心十 ) , A Z ( + ) , ( 9 ) 、 ( 1 6 ) 可知 C : 。 ( , ) 一 ! A 二 ( 十 )N0 ( : , , ) * + i c ` : 一 1 , 2 , 3 J a 口 成 ( + ) 为定义在 口石乡 上的实函数 卜C : 、 价 、 C 3 为 实常数 , ~ C : ~ C , ~ 叭 。 为一正整数 , 二的选取与边界 条件有关 , 一 ( 1 9) 根据条件 在夹层板 间题 中 。 》 3 , 在本文以乍的算例 中我们取 , ~ 占 (并不是 必要的 ) . 把 l( 9 )式代入 到 s( )和 l( 7 )中 , 可以写电 : F ( 二 ) ` 肠r边 ;汗) , A Z ( + ) , 2 1 f( 幻 ~ 肠 [浅 ( 十 ) , 习 , - ( 2 0 ) ( 2 1) 其中 L ; , 肠 均 为积分算子 : L , ( A ; , A Z , : ) ~ R e 塑 瓜voI ds _ + { 儿枷 、 一 犷 ’ 二 护 了刃奋 _ 不J ō尸`.、J 一君公 气决r 。 ( A 3 , : ) 一 ZR· {! a , 一 孙 ! 。 阶瓜如 ,“ “ 从 一 争 ( ` 一 ; ) }外 “ } ( 2 3 ) 由于边界条件 ( 3)一 (” 均 可由 F 汀 表 出 , 把 ( 20 ) 、 ( 21 )代 人进去 , 并令 , 一 “ ` 冲 · 我 幻可得到以 石( 十 ) , 成( + ) , 滩式+ ) 为未知 函数的边 界积分方程( 见附录 ), 简记为: 、 , · 了、 ` 门、é 厂气奋` 嗯二乙, 、 L , 。 ( A : , A Z , A 3 , : 。 ) ~ o 从 ; (才; , A ; , A , , 二 , ) 一 , 0 宕。 〔 口蔚多 勒夕口尹

166 力 学学 报 (1990年)第22卷 Lw(A1,A2,A3,z0)=020∈a (26) 对Hoff型夹层板,柳春图引人三个函数F、F1、f表示其基本方程和边界条件: D△2F。=q (27) a1-,-一K高. (28) D(1-)△f-cf=0 (29) 2 其中: D=D十2D1, D-E(ht E 2(1-) D"1z-历' K-C(D+2D2,C-G.(hi) 2DD 4、E;为表层的泊松系数和弹性模量。k、¥为夹心及表层的厚度。G。为夹心的剪切模 量. Hoff型板的边界条件亦可用F。、F1,f表出 用类似上面推导Reissner型夹层板相同的方法,可知(27)一(29)的齐次一般解为: F。=Re[xp(x)十p(s)] (30) P,-2Rel()Reta( (31) 2 1-etm( (32) 而相应的边界积分方程可简记为: H(A1,42,A,44,x)=0z∈6②1 (33) H(41,A1,4,A4,)=0∈0g②, (34) H(A1,4,A,44,0)■0o∈8项, (35) 三、数值结果 根据本文推导的边界积分方程,我们用线性边界单元编制了程序,并对一些典型算例 给出了数值结果. 表1两邮边售支另网边园支方板受均布背酸 2DfD。=10- WRm(10-2q@/D) MR=(10-1ga2) wa(需) Mu() 本文解 [3] 本文解 [31 本文解 本文解 ,005 ,2568 .257 -.6346 -.637 .2547 -.6366 .010 .3007 ,301 -.6052 -+608 ,3002 -.6073 .020 .3847 ,385 -.5626 -.567 ,3792 -,5701 .030 ,4653 ,467 -.5359 -,536 ,4547 -.5412 .U40 ,5461 .547 -,5089 -.514 .5348 -.5214 .050 .6243 .626 -,4893 -.495 ,6051 =.5005 ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
力 学 学 很 ( , , 0 年 l ) 第谁里 卷 L试 A : , A Z , A 3 , 0)z ~ 0 : 。 任 。` 多犷 - 一 价6 ) 对 H o f 型夹 层板 , 柳春图 引人三个函数 0F 、 F , 、 f 表示其基本方程和边 界条件: D泌 , F 。 ~ 宁 ( 2 7 ) △ F : 一 灸 Z F ; ~ 一 q 笠艳力。 ( 2 8 ) l 。 ( z 一 , , )△ r 一 ` r 一 。 2 ( 2夕) 其中 0D ~ D + Z D t , , , C ` D + Z D , ) 刀吸一 ~ 一 一= ~ 一 一一 ~ -一 -` ` 舀 , Z D r D D _ 马些 一土止 _ D ` ~ 一鱼立一 . 一 找 1 一 心) ’ 一 ` 1戏士` , 分 ` 仁 一 ~ cG ( 方 十 、 ) ’ 人 , , 、 E , 为表 层的 泊松系数和弹性模量 . h 、 t 为 夹心及表层的厚度 . G , 为夹心的剪切模 量 . H of f 型板的 边界 条件亦 可用 F 。、 F : , f 表出 31[ . 用类似上面 推导 R ie s s ne : 型夹层 板相同的方法 , 0F ~ eR [ : 种 1 ( 幻 十 物( 幻 ] 可知 ( 2 7 )一 ( 2 9 )的齐次一般解为 : , , n , 、 , K z 一 「 ` . _ , , _ 、 , , , 「 扩 _ ~ l 、 _ 、 1 , _ 厂 1 一 ` 长 e L甲叭幻 J 一 叶 “ 、 _ 仄。 L 公甲3 、 盯沪 J 匆。 l 一 二 苏 , 、 i 一 2 J . L , ` 少 1 J盯 ( 3 0 ) ( 3 1 ) r 一 Z R e [叭 ( , ) ] 一 兰 “ !: eR 〔。 `一 , , “ “ ! 一 价sl( 一 好` 一 ` , , ) 而相应的 边界积分方程 可简 记为: 日函 ( A t , A : , 汤 , 减 , 九) ~ 。 踢浅A : , 八 , 通 , , 瓜 , 如) ~ O U 材 ( A , , 滩: , 冼 , 再 , 勒) “ O 忿. 〔 口石多、 岁. 〔 O困 : 名. 〔 6 石多, (封 ) ( 3 4 ) ( 35 ) 三 、 数 值 结 果 根 据本文推导的边 界积分方程 , 我们用线性边界单元编制了程序 , 并对 一些典型算例 给出了数值 结果 . 丁 表 1 两那边蔺宜 另两边翻交方板级均布扮旅 2马阳 。 二 1丁 , 砰二 , ( 10 一 2叮a ` / D ) 本文解 〔3 〕 胭双 . ( 10一 l 甘a Z ) 本文解 〔 3 1 。 0 0 5 。 0 1 0 ` 0 2 0 一 0 3 0 , 2 5 6 8 . 3 0 0 7 。 3 8 4 7 。 4 6 5 3 , 5 4 6 1 。 6 2 4 3 。 2 5 7 。 3 0 1 。 3 8 5 。 4 6 7 。 ,呼 7 . 6 2 6 一 。 6 3 4 6 一 . 60 5 2 一 . 5 6 2 6 一 。 53 5 9 we 。 , 0 8 , we 一 4 8 , 3 一 , ` 3 7 一 , 6 0 8 一 , 5 6 7 一 , 5 3 6 一 。 , 1 4 一 。 4 , 5 . 0 4 0 一 0 5 0 。 3 7 9 2 。 4 , 4攀 , , 3咦吕 。 的 , 1 一 、 5 7盯1 一 . 当41 2 一 。 , 2 几4 一 。 50 05
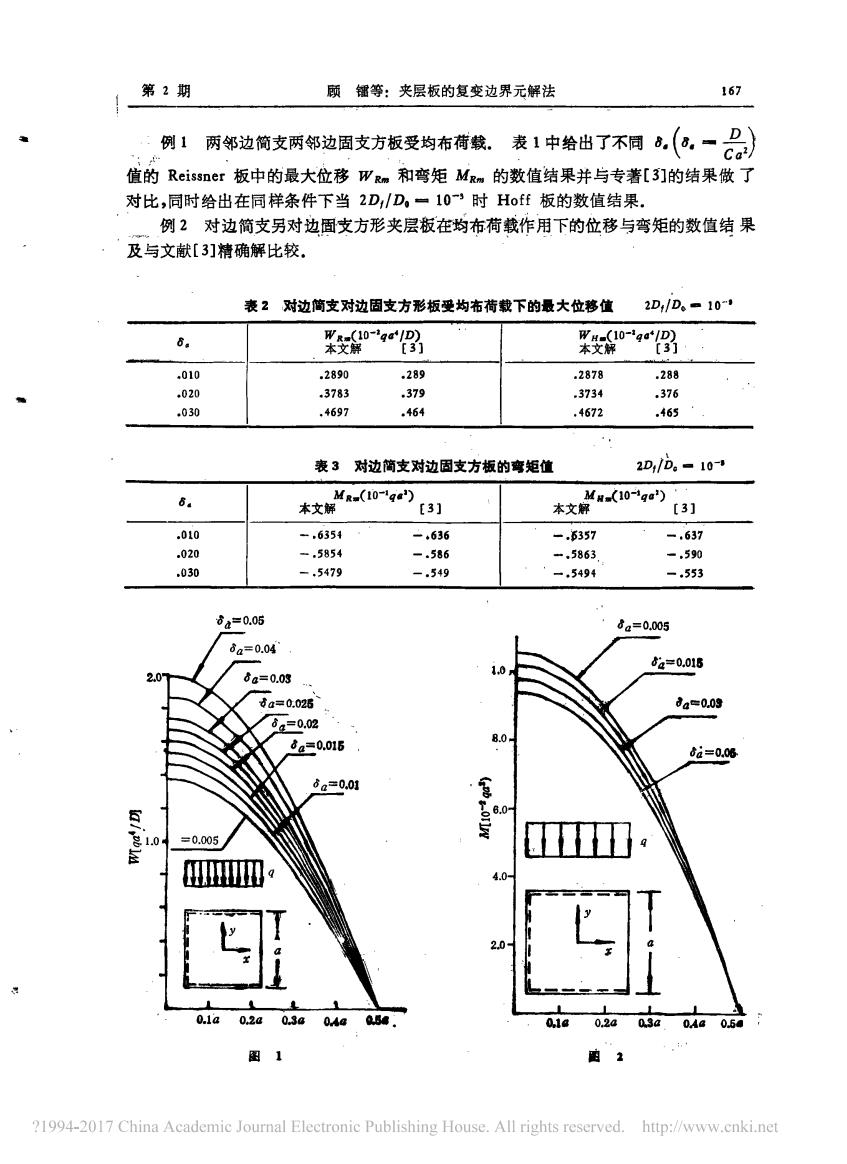
第2期 顾镭等:夹层板的复变边界元解法 167 例1两邻边简支两邻边固支方板受均布荷载。表1中给出了不同8(0,一》 值的Reissner板中的最大位移WRm和弯矩MRm的数值结果并与专著[3]的结果做了 对比,同时给出在同样条件下当2D,/D,一10-时Hoff板的数值结果. 例2对边简支另对边固支方形夹层板在均布荷载作用下的位移与弯矩的数值结果 及与文献[3]精确解比较. 表2对边简支对边因支方形板受均布荷载下的最大位移值 2D/D。=10 6. 米0r8 WH-(10-iga/D) 本文解 [3] ,010 ,2890 ,289 .2878 ,288 ,020 ,3783 .379 .3734 ,376 .030 .4697 .464 .4672 .465 表3对边简支对边固支方板的弯矩值 2D/D。=10- 6. MR-(10-1g) Mn(10ge2): 本文解 [3] 本文解 [3] .010 -.6354 -.636 -,5357 -.637 .020 -.5854 -.586 -,5863 -.590 .030 -.5479 -.549 -.5494 -.553 da=0.05 6a=0.005 6a=0.04 1.0 6a=0.016 2.0 a=0.03 da=0.025 da=0.03 62=0.02 da=0.016 8.0- 6a=0.08 6a=0.01 =0.005 4.0 20 0.1a02c0.3a04aa84. 01 0.2a0.3a0.4a0.5 图1 由2 ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 2 期 顾 镭等: 夹层板的复变边界元解法 例 两邻边简支两邻边 固支方板受均布荷载 ; . 表 1 中给出了不同 , , f ` · 共、 、 ` a 一 / 值的R e is sn e f 板中的最大位移 二: , 和 弯矩 坑 。 的数值结果并与专著’3[ ]的结果做 了 对 比 , 同时给 出在 同样条件下 当 Z fD / 0D ~ 10 一 , 时 H o f 板的数值 结果 . 例 2 对 边 简支另对边固支方形夹层板在均布荷载作用 下的位移 与弯矩的 数值 结 果 及与文献 【3] 精确解 比较 . 表 2 ZD , / D 。 . 1 0 一 ` 8 。 司 . . 姗曰旧口舀沁` 山` 勺一 一 ` ~ ` .` ` 一 二` . ~ 曰` 一 0 10 一 0 2 0 . 0 30 对边简支对边固文方形板受均布荷载下的最 大位移位 , 加 (10 一 协 ,lD ) 一 } 朽-l( 本文解 〔 3 ] l 本文解 0 一 , 叮。 ` / D ) [ 3 ] 一 2 8 9 0 一 3 7 8 3 。 4 6 , 7 。 2 8 , 。 3 7 9 。 46 4 。 2 8 7 8 . 3 7 3 4 . 4 6 7 2 一 2 8 8 。 3 7 6 一 4` , 表 3 对边 简支对边固支方 板的宵矩值 z刀 , /石 。 一 ; o” M如〔10 ` 场护 ) 木文解 【3 ] 古在= 0 . 0 5 一 . ~ 妞 . , 门口 一 . . , 匕公 . 一 沙a = 0 . 0 6 吃 = .0 0 16 ` . 氏O, 峪 = 0 .哈 犷川 川 · 6 窗写,。工 有、苗 ,急 丁f · 1 去1咖 .0 l a .0 2 a U a 叼 ` 么翻 圈 1 认 1召 .0 2召 曲 1 . 占~ ~ 一 - 目目 0 . 4召 Oj

168 力学学 报 (1990年)第22卷 例3三边简支一边自由方板在荷载(均布)作用下的数值结果,图1、图2分别给出 了Reissner板沿自由边位移和弯矩在不同8,值时的曲线,表4给出了最大位移及弯矩 值 表4三边商支一边自由Reissnor坂的数值结果 6. WRm(10-1qa/D) MRm(10ga) 本文解 [3] 本文解 31 ,010 .1462 ,146 1.037 .020 .1601 .160 1.003 .030 .1734 .174 .9773 ,050 .1993 .199 ,9384 附录 利用公式: 0C2=2Re8C2, C2=21m Ox 03 0 02 4()=40( a(2-0℃)-2i02=402 0202 8x2 8y2 6x0y 082 我们可以把Reissner型层板中的广义位移和广义内力写成以F,f表示的复形式: :=2Re OF 68 +21mt 元 中,m2lm OF -2Re 01 8元 08 4D dF c 0x03 M,=-4DRe{(1+)F 0x0屈 +1-(腊-器} M,--4DRe {1+) 82F 0z0足 -1-(腊-器} M,-201-1m(g器 - 62/ Q,--2DRe OAF -2CIm of 8东 8话 ,=-2DIm AF+2CRe of 0 在边界上,有: M.-4D++1-c-(器-影) +-n(-】 082月 -20c-[-m(-i8) 02 ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
力 学 学 很 〔1 9 9 。 年 ) 第 u 卷 了 值 。 例 三边简支一边 自由方 板在荷载 3 ( 均 布)作用下的 数值结 界 凰林段2 缝鬓笃给出 Re is e rn 板沿 自 由边位移和弯矩在不同 。 。 值时的 曲线 , 表 4 给出了最 大位秘渔弯 矩 裹 4 三边简文” 边自由 R . 如“ r 板的欲位编泉 肠左` ( 妞誉卯今 本文解 r 3 1 1 . 0 3 7 l `心0 3 . , 7 7多 。 夕3 8 4 一 8 。 。 0 10 。 0 2 0 。 0 3 0 。 0 , 0 平 , , ( 10 一刀甲` 4 / D ) 本文解 「3 ] . 14 6 2 。 1 4 6 . 160 1 . 1 6 0 . ! 7 3 4 。 1 7 4 1 9 9 3 。 1 , 9 附录 利 用公式: 匹二立一 z R e 口盆 一 旦交二 _ lZ m 旦立旦 o y d牙 △ ( … ) ~ 4 d Z ( 试… ) a 牙 … ) 少( ~ · ) 少介 · ) _ _ , ; 一 - 一 — ` . 口考口牙 口x Z 口y 里《兰2 _ 4 翌纽2 d 功y a 牙 2 我们 可以把 R e * s s n e r 型滩层 板中的 广 义位移 和广 义内力写成以 ; , , 表示的 复形式: 沙 丝孤一旅af 二 一 : R。 塑 + : Im d 云 沙 , ~ Zl m 一 Z R e 即 ~ F 一 口 Z F a 七口牙 丝孔4D一c 。 : 一 、 R 。 { ( ` + · , ) a Z F 口盆 d 牙 + (一 , f ) 二 , J , n 「 , , . 、 口 Z F , , 、 止粗 , - 一 牡 声入e 、 气1 , 1. 少了少 — 一 L l 一 少 f j , L 一 ’ ` ’ d z d 三 ’ ` ’ 叽 一 2 ” ( , 一 咖 m (器 一 `器) Q : ~ 一 Z o R。 g , ~ 一 ZD I m a △ F 一 口若 口△ F a 云 一 2“ `m 器 + ` “ R· 器 在 边异上 , 有 : 从 一 ` “ l “ + 一 ,器 + ` , 一 ,“ 2二 , 2 , R· (器一 ;器) 二 , · , _ . 、 _ , , _ 了护尸 _ ; 护 f 、 1 ` 、 ` 一 配 ] / 扮口 “ “ 二 毛 二 二丁 — 一万二刃 曰 人 d 佘` 口 君 ` Z丁 从 ~ 一 Z D ( 1 一 , , ) ` , 2 _ __ _ _ 八 、 _ / 口 Z F _ _ ; a 兮、 、 ` 一 ’, J“ u 冤一三二丁 一 , 一 二丁二 ~ 刀 \ 口劣 . 口 右` /

第2期 顾镭等:夹层板的复变边界元解法 169 +4mlRe( 器-:8器】 0z2 Q.--2D(Rea≌E+mim) -2R:8+mm a短)+2(1m -mRe Of) 08 8元) -2(iIm -mRe 02 头+mlm 0 0: R 4D82F C 030 把正文(20)、(21)代入以上各式,我们可得到用边界未知函数A(+),A(+),4(+) 表示的边界点的广义内力和广义位移,简记为: 21 M。=M(A1,A2,A,x) M,M(A,A:,A.,z) 2。=r(A,A2,A,zo) 中。=F(A1,A2,A,20) 中,=F(A1,A2,A:,20) w=Fw(A1,A2,A3,20) 边界条件要求: Fw=0一地*,Fm-币。一中,F,=,一中t.zo∈8项 Fw=而一w*,,Mn=M。一M,F,=中,一中.∈O功2 M,=M,-M,M。=M.-M体,r.=豆。-Qt.∈O功, 其中w*,M,M,中,中Q。为由特解F*所确定的函数,以上三式亦可简记为: Lo(A1,A2,A3,z0)=080∈0项 Lw1(A1,A2,A,z)=0zo∈8项 LM(A1,A2,A,0)=0z0∈0项。 参考文献 【1】淮“I,椭圆型方程新解法,上海科学技术出版社(1963). [2】隐r海里什维里,奇异和分方程,上海科学技术出版社(1966), [3】中到科学院北京力学所,夹层板壳的弯曲、稳定和振动,科学出版社(1977). [4]Hromadka,T.V.,II,The Complex Variable Boundary Element Method,Sptinger-Verlag (1984). [5]Hromadka,T.V.,II,Guymon,G.L..CVSEM:Development,Int.J.Num.Meth.Eng.20.1984) 25-37. [6]Hromadka T.V.,II,G.L.Guymon,CVBEM:Application,Int,J.Num,Meth,Eng.21,(1985) 1013-1025. [7」胡海昌,各向同性夹层板反对称小烧度的若干问题,力学学报,6(1963). f8】 柳春图,夹层板方程的变换和四边简支矩形夹层板的变形问题,力学学报,8,4,(1965). ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
+ ` m `R · (器 一 `器)! 。 一 2 可` 臀 十 ` 瞥)` C 一 卜器一” 影 办一 2 卜 器杨恤 黝 十 , ( 六 l l m豁一eR 黝 丸 一 2 ( lmI 器一叙 影 一 , (枷 ` 一 ’ 一 誓器 翼 十 , 恤 a 云 擎、 口云 / 拍正拟 2 0) 、 (lz ) 代水以上 各今 我们 可得到用边界未知函数 一 , , (+) 表示的边界点 、 勒 的广义内力和广义位移 , 简诅为声 补 ; M ` ~ 一 呱( 才 , , 诫 2 , A , , 八 ) . - M, , M犬 A“ A Z, · A 、 , : 。 ) Q一 二 .( A : , 气 A Z , A , , : 0) 沙 。 ~ F . ( A : , A Z , A 。 , z 。 ) 沙 : ~ tF ( A , , A Z , A , , 勒 ) , ~ F , ( 才、 , A Z , A , , z 。 ) 才: ( + ) , 才, ( + ) 边界 条件要求: F留 一 谕一 , 气 F 。 一 子 , 一 山: , F : 一 必 , 一 对 . : 。 。 a必 : F , 一 而 一 , * , M 。 ~ 丽 。 一 M 育 , 矶 ~ 少 , 一 对 . : 。 〔 a 必 2 M , 一 丽 : 一 衅 , M 。 ~ 丽一 瞬 , 二。 ~ 口一 Q育 . 勒 ` 。必 , 其中 。 气 毗 , 孵 , 此 , 对 Q 。 为由特解 F * 所确定的函数 , 以上 三 式亦 可简记 为: L , 。 ( A : , A Z , A 3 , z 。 ) ~ 0 L o l ( A , , A Z , A 3 , : 0 ) ~ o L M ( A : , A Z , A 3 , : 。 ) ~ 0 名。 〔 a 必 万。 〔 O必 君。 〔 口必 . 参 考 文 献 s P r i n g e 卜 V e lt a g ( 19 3乌、 ` M o t h . E n g . 加 t 、 19 8 4 ) 、 1J. . ,. ù , 由,J」.盆 二弓23 曰, M e t h , E n g . 班 , 吸1 98 5 ) L 石1 [ 7 」 炙8 〕 维本 ’ I , 椭圆型方程新解法 , 上海科学技术 出版社( 19 6 3) · _ 黔戳霎粼藻撬裳馨柔禁袭黯溉擎( ! 97 , : , ` , , H r o m a d k a · T · v 一 11 , T h e C o m p l e x v “ ` i “ b l e B “ u n d ` r y ” “ m e n , 竺佗-at o o , H r o m a d k a , T . V . , 11 , G u y m o 。 , G . L 二 C V B E M : D e v e l o p m e n t , l 几 t . J . N u 口 · 瑟二二 d k 。 T . v . , : : , 。 、 L . 。 。 , 。 。 n , 。 v B E M : A p p ; 、 。 : t ; 。 n , , n , , J . 、 · m , 霖馨量:复霆履毖霆暴霎履凳纂轰篙类霆纂夏翟篡霹篡盆 , 髦攀辈毅, 8 , 4 , ( 1 9 6 5 ) -

170 力学学报 (1990年)第22卷 A COMPLEX VARIABLE BOUNDARY ELEMENT METHOD FOR SANDWICH PLATES Gu Lei Huang Maokuang (Universisy of Science and Technology of Ckima) Abstract In this paper,we will discuss the complex variable boundary element ap- proximation for sandwich plates.The general solution of Helmholtz's equation in complex fi- eld has been discussed in detail.Based on the Vekua's representation of analytical function,we set up a new type of integral equation for problems of sandwich plates,and use boundary ele ment method to solve this integral equation.The numerical results of some standard problems of sandwich plates are in good agreement with those obtained by analytical method everywhere in the solid including the region near the boundary. Key words BEM,sandwich plate ?1994-2017 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
1, 0 力 学 学 报 ( 1 , 90 年 ) 第 J 之 一 鑫 A C O M P L EX V A R I A B L E . B O U 加 O A R丫 E` E M困 N T M E T HQ D F O R S A N D W! C H P L A T E S G u L ie H皿 n g M a ok 助。 g (U 耐 , 翻妇, 可 舀d `胭 筋日 T“ 汤耐 口妙 of C石 . ) A b s t r a e t x n th i s p a p e r , we w i l l d i s e us s t h e c o m p l e x v a r i a ble 长扣n 面 r y e l e m喊 a 卜 P r o x i m a t l o n e l d 五a s be n S et u P a n e w 功e n t m e t h od o f s a n d w i e h l o r s a n d w i e h p l a t e s . T h e 它 e n e r a l 5 01 以 i on of H e l功h o l该、 德。 u 肚ion i n e om o l德燕 林 以l s c 雄s e a I n d e t a l l · b a s e d o n t九e v e 盆 u a 一 5 r e P r e s e nt at l 如 叮 吕。 创尹宜亡扭 I t u n 改 10 残 钾. ty件 o f i n t e g r a l e q u a t i on f o r p r ob l枷 of s幼d初c h p l瘫自, a o d 二 加。 点d短呼 日` t o s o l v e t h i s i nt e g r a l e q aut ion . hT e n um e r i C a】 r se u l ts of 5 . 的七 成 幼d ar d p r比l e耐 pl a t留 a r e i n g o o d a g r e e m e n t w i ht th o s e o abt ine d by a n a l外 ic a l 口d 五od ve e r y 甲b e r . i n th e s o l id i n e l u d i n g t h e r e g i o n ne a r th e b o u n d a r y . K e y w o r d s B E M , s a n d w ic h 禅at e