
第一章 平面问题 §1一1直角坐标下按位移求解的控制方程 当取用直角坐标系x时,求解弹性力学问题的基本方程为 平衡方程 密+旁+X0,旁+密+Y=0 (1.1) ay ar 几何方程 6=器6=多如=密+旁 (1.2) 物理方程 对于平面应力问题: 5-意a.-g,6w2%,-o,=21吉0, (1.3) 或 =+e,、=+、o=2a年14 E E 对于平面应变同题则须将式1.3)和1.)中之E澳为山换为1己。 首先讨论平面应力问题的控制方程。 将式(1.2)代入式(1.4)中,再将式(1.4)代入式(1.1),有 (整+器+告离》+x0 2ax动y (1.5) 要+1要+生*+-0 式(1.5)耶为传统的弹性:学平面应力间题求解位移分盘4和v的控制方程。 引入体积应变函数对平面应力问题 6=6+6+=二兴,中)-二2+ (1.6) 利用式(1.6),式(1.5)可以写成 a品器-票+号装+x=0 (1.7) 20年经+器+品》-r-0 如果将式(1.7)中之e也视为独立的未知函数,u、v及e三个函数须由式(1.6)及 (1.7)的三个方程确定。为了我们的目的,利用式(1.6及(1.7)之关系推导另一个求解e的 方程。 分别对式(1.?)第一式及第二式分别关于x和y求一次导数,然后相加,并利用式 1

(1.6),可得 a+品-整++器+器-0 (1.8) 式(1.8)就是我们所需要的求解e的方程。从而有求解u、v及e的如下控制方程组: Vie= +”4-(警+) E yu=-12证 1+”-21+"2x (1.9) w-甘品器-2吉y 式中 =是+易 控制方程(1.9)的优点是非耦联的。先由第一式求解e,(其中X和Y是已知函数),然后 将求解得的e分别代入第二式第三式中求解4和,这样,所求解的均为独立的二阶偏微分 方程, 进而采用如下无因次量: (z,)=(xy》,(a,)=129(uw)} a (a,)=且+是-20(a,n) vE (1.10) (8,)=1+1-2w(x,Y) DE 式中a为特征长度,取作参考值。于是,我们有确定无因次量函数m、⑦及:的如下无因次控制 方程: 7=-竖+ 7z=一1十v速 -2x (1.11) 7行--1+" -27 穷 式中 e与、五间的关系为 -之器+》 (1.12) 利用式(1.10)之无因次盘及关系式(1.12),由式(1.2)及(1.4)可得如下无因次应力一 位移关系: 可,=+爱马,=+需w-需+) (1.13) 式(1.11)一(1.13)即为以下求解平面应力问题时所使用的控制方程和关系式。 用同样的方法可得到如下平面应变问题的芝制方程:

7e=- 爱+ a取 7五=一 -2X (1.14) U委 7师=一1重 v万 -2? 在此情形下,e与立、五间的关系为 =“鑒+》 (1.15) 而应力一位移关系仍与式(1.13)相同,大是其中e应按式(1.15)计算. 下面利用有关控制方程和关系式求解若干在何题,并闻明求解方法的原理和步骤。 §1一2两端固定深梁的应力分析 知图1.1(a)所示两端固定深梁,夸长2a,梁高2b:梁单位体积重为Y;梁的上边界受竖向 分布荷载q(x);粱的受力属平面应力问题。 取用如图所示直角坐标系x。不失-一股性,设荷载q(x)关于y轴对称,即q(x)=q(一 x), (r) a】 图1.1 取用半跨长a为参考长度,在式(1.10)无因次壁的情况下,并将荷载q(x)转化为无因次 孟定)=宁-2必g(e),则图1.1(a成为图1.1(6),图中A=/a. vE 注意到体积力为梁的自重,则8=0,?=-7=1+)一2)y),控制方程(1.12) 成为 7=0,7a=-1÷爱,7元=-1等+27 (1.16) 为了简化计算,将图1.1(b)所示之荷载分解为如图1.2(a)和(b)所示关于轴云对称和反 对称两种滑形。 由图1.2有如下边界条件: 对称荷载情形[图1.2(a)] 王=士1,8=0、0=0 (1.17) y=士A,6,=-i(x),=0j 注意到式(1.:,条件(1.17)可写成
49 D (a) (6) 图1.2 -士1,a=0,五=0 =士需=--到, (1.18) 反对称荷载情形[图1.2(): 元=土1,元=0,节=0 节=士1,a,=干,(),如=0 (1.19)· 注意到式(1.13),条件(1.19)可写成 受=土1,0,石=0 了士A,需=-8干(动, 而 而 而 (1.20》 (一)两端固定深梁应力分析的边值问题 综合控制方程(1.16)及边界条件(1.18)和(1.20),两端固定深梁应力分析的问题归结 为如下单个偏微分方程的边值问题: 对称荷载情形[图1.2(a)] 1, 72e=0, (1.21) 主=±1;e=();y=土A,e=f,() 其中f()及f(云)为待确定之函数, 2. 7m=一1十"使 ”—妥 (1.22) 元=士1,a=0,3=士A, 3. 7元一-1十v速 污 (1.23) 天=士1,元=0:y法士1, 的 =一“4() 反对称荷载情形[图1.2(b)] 1. 7e=0 (1.24) 主=土1;e=g1(灯);y=士,e=士g,() 其中g1()及g()为待确定之函数. 2- 7z=-1土”更 u委 (1.25) 交=士1,=0;寸=士入, 证

3. =-1+需-27 (1.26) =士1,=0习=士,需-千)】 (二)对称荷我情形下的解答 1.求解 将式(1.21)中之待确定函数f()和f,()表示为如下级数形式: fig)=Aeo5、f国)=2 B.cosa.F (1.27) 式中A,和B,为待定系数,a=(-0.5)r,c,=(i一0.5)x/2 于是,由式(1.21)有 整+琴=0 元=士1,=】 ea, 5=±d,= 豆awa (1.28) 不难验证,边值问题(1.28)之解为 i- cha2cosa迈+B,cosTha.] cha (1.29) chaA 2.求解云 将式(1.29)代入式(1.22)中,有 bs5-B,气sina7ha cha chaA (1.30) 乏=士1,z=0: 可=士, 需-爱 用有限积分变换法求解边值问题(1.30),并取用如下积分变换式: 正变换: (a,)=t'a(G,5sin日,zd2 (1.31) 逆变换: (往,)= *(9,sinp年 式中 月,=次 以sin月:王乘式(1.30)之两端,并从一1到+1对云进行积分,有 器-=-1245-8 ”.- cha chaiA (1.32) )=士A, 需-一要nz近 式中E对='sha'inf,zd左=-2eo且 Fsinain tintin j- a3.+ 一月与 高+月 注意到”为y之偶函数,式(1.32)第一式之解为

C[AEcoa3+B.F,chay] (1.33) 式中 E=1+v +cha'4=1十"aPg G u (a-B)cha; C;为积分常数,由式(1.32)第二式之条件确定,即 C,sh,A- Ae Buineh (1.34) a-[1,n82,j=123“ 将式(1.33)进行逆变换,有 五=小 Cb+AE.oaB chsing (1.35) 3.求解节 将式(1.29)代入式(1.23),有 察+察-1÷2[Ah会-a] cha. chad (1.36) z=士1,可=0:=士d, 需=-宫ao一ae到 仍用有限积分变换法求解边值何题(1.36),并取用如下积分变换式: 正变换: a5=scajcoseza (1.37) 逆变换: (云,)=】 *(g50e8,年 式中 a,=(j-0.5)x 仿求解z的方法,最后得 =- [君i-8L5-Hh5)+ aeha,cosa元(1.38) 武中 L,= 品a[若岩1+e,aha,0-1小,G,=1中”cC a,chaal 2u u (ataj)cha G-242,,-岩aay=ctz2 +1 (a+a) 4.确定常数A,、B.及C 式(1.29)、(1.35)及(1.38)中A、:和C尚是未知的,还需要确定,常数A:,B,和C,之确 定,除利用条件(1.34)外,尚须利用如下两个条件: z=士1,=2器+》 (1.39) =士,=2毫+} (1.40) 利用条件(1.34)、(1.39)及(1.40),最后得到确定常数A、B和C,的如下线性代数方程 组:

Ax-2axw-2cNwA-0】 a占-28X-2c0eh队=-ai-123 (1.41) 宫X+2-CAA-z 式中 x.cop YP cap.ouFche GM,jsindd,YM(Lahed-HehA)-aiF ,sha 乙-会a恤a-二2-a2,Ny- 2a,'chB;Asina,'A 4-月4 4十月, A(a+) P-2微.Q-2+如a+2 8-月) 4÷9; 5.应力分量 由求解式(1.41)之方程组确定常数A.B,和C后,代入式(1.29)、(1.35)和(1.38)中即 可进行计算、元和元.再将式(1.29)、(1.35)及(1.3)之、和云代入式(1.13)中,则得到如 下应力分量的表达式: =含A22+2oa4与j+2a可 cosaIcha,y chak F.o chaCdcoach3 -言4出-身6awj+亨 cha chaA +ah-)ciaj-aaa5oa到-月2e2as2 chajA ,-吉42 o.Guiaw--48 in sianl5 2auh9-a7n-28a ais S asinah enaA (1.42) (三,反对称荷载情形的解答 将式(1.24)中之待确定函数g,(⑤)及g:()表示为如下级数形式: a-立un或a)-2aca (1.43) 式中A:和B为待定系数;4=(i一0.5)π,'=证/A, 仿求屏对称荷载情形解答的方法和步獠,不难得到反对称荷载情形的解答、这里略去演 算过程,直接给出有关的表达式和算式

1、、z及节的表达式 i一2[A087+& che sha 五=} Cabg+in 可=】 Gucopcco a.sna. a (1.44) 式中E,=1+" BEd ()ch E=-2cs8.Fw=1上”R +防 )shad n8-A》_照2,G=200,H,=号a c一甲; a十P; 时十2 G=1+"3C ”(+chR: 乙= 8ia0H,(eha以+echa)-i小, -」a国cs边 2. 确定常数A、B:和C,的线性代数方程组 AXt一】 aXw-含cANa明-0 &片-2a,r1-cp0sh以=-a g=1.3,3,… (1.45) 2AXs+宫aY中C.RckpA=-一z 式中 2,F.Quhe以 x-[以E-含c41o8 Ywy ajFxchaj-a;M:(Lcha,a-H;isha;) z-24[品+-2牛 (+;) =2,R a4+9 (+:) a,=ia6a二2+ia+82,A= a-B; a +Bi 3.应力分量表达式 -2A25-空Ao2an]+会王2 shai FC.co.p3 -24费盟-2灯]+2a4器 ak +Ealsho.y:H.(sha3+achay)cosa 月222 shaid

:Eininop B.asin(L.cho3-H.ho.)aF sinp,tche] +2caah5+2[2+]aa (1.46) 利用上述解析解,我们对两端固定深梁的应力进行了具体的数值计算,计算分为两种情 形:一为深梁只受均布荷载g0而无自置,即g(r)=g,7=0,并取6=1+一202,一1.0, E A=1.0,=0.16?,计算结果绘在图1.3上,如实线所示者,另一为只有自置Y而无外荷载,即 g(x)=0,并取7-1+)9-202y=1.0,=1.0,=0.167,计算结果绘在图1.4上,如实 DE 线所示。 0.53 0.81(053) 2.01 1.00 1.00 0.28 0.00 0.00 a0. [0.75) (1.41) 0.98》 (Q96)Y(0.36】 10.0LJ (0.11) (a07) ⊙ ⊙ 0.18 0.07 0.16 0.87 074 10.01 0.00 0.36d 0.0 t0.18)© (0.04) 0.11) K0.87可 (073 (0.02) (0.057 (0.35】 (0.74) p 9① 0.01 ④ 0.03 o17: 0.45 0.33 003*7409 3 (0.01) (0.04) 0.141 ■0.5)■ ● (0.33) 0.025(006 (q31) (0.42》 a① 0.01 0.12 a10 0.10 0.03 10.00 0.21① 08 f0.06》 (0.1)⊙ (0.1y o.1i)© (0.105 (0.c2) (c.04) 〔c.20) (0.27) ⑧ ⊙ Lf0.32 从.出 0.00 0.ou 0.04 0.00 0.00 a00 (0.29) 0.1g) 1.04 0.01) (0.c0) (0,05) o.o1) (0.071 (a.l) (.51) (a 可,分灌图 (b) ,分布西 (c】 「,分布阳 注括母()内的值为有限元结果 酒1.3 背复应力分布厨 为了验证解析解的正确性,对上述两种荷载情形下两端固定深梁的应力,我们又采用有 限元法进行了计算。计算中利用问题的对称性,取深梁右半部分为计算对象,单元划分如图 1.5所示,并利用SAP5程序进行计算.计算结果也分别绘在图1.3和1.4上,如避线所示.由 图可以看出,解析解与有限元结果吻合良好,证实了解析解的正确性。 为了检验解析解中级数的收敛情况,我们在计算深梁只受均布外荷载的应力时,分别取 级数前10、15、20、25、30项计算了x=0.5裁面上的应力。计算结果列于表1.1,1.2和1.3 中
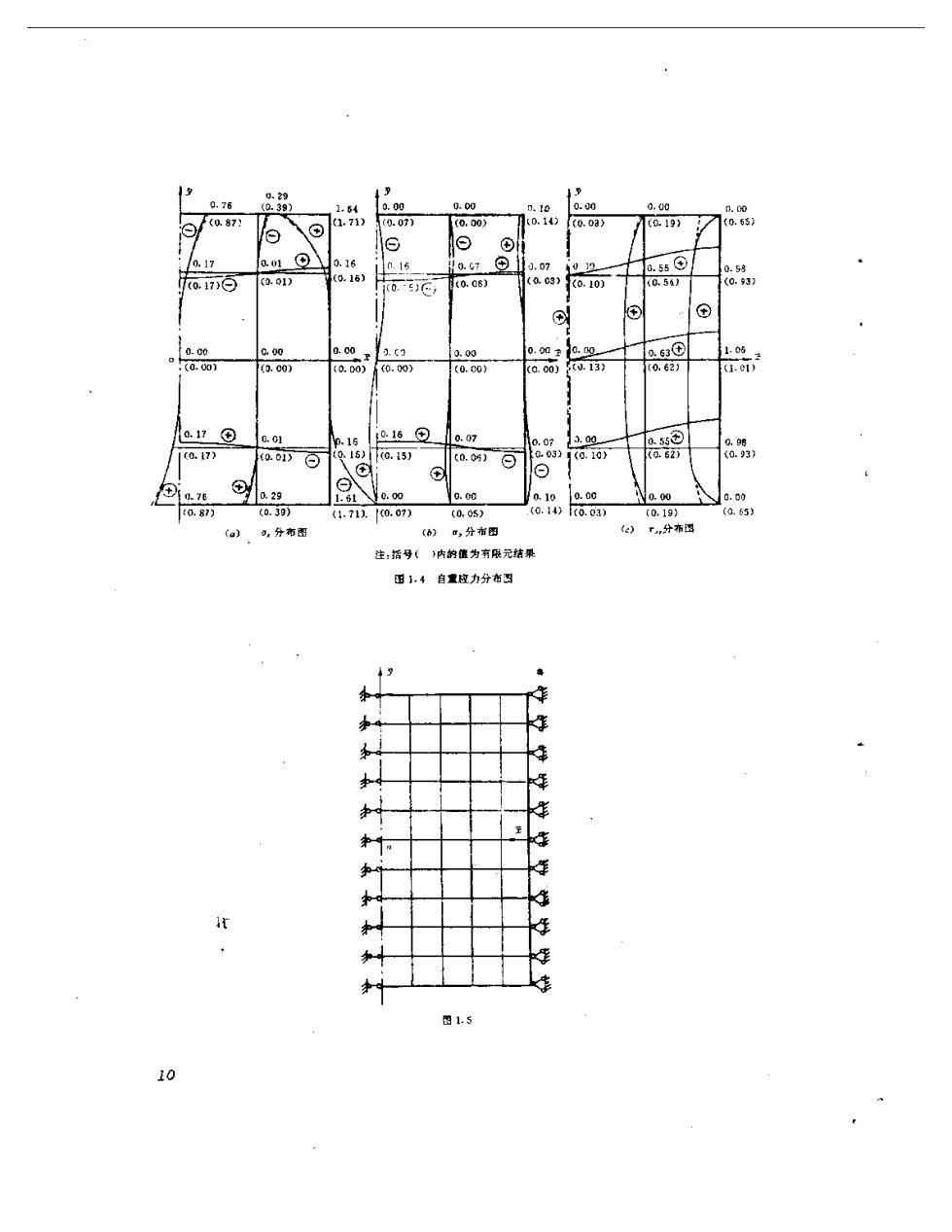
0.29 0.76 (0.39) 1.54 0.00 G.00 D.10 0.00 0.U0 0.00 (087】 (1.71) (0.07) ⑥ 0.00 0.14 (0.0 (0.19) (0.6$) ⊙ ⊙ 0,17 0.01 ⑨ 0.16 0.15 0.7 .07 0.55⊙ 0.s fo.7百 (0.01) (0.16) 0.5)Ci (0.06) 0.c3) (0.10) (0.54) (0.93 ⊙ ① 0.00 00 0.0 .1 0.00 0.00三 a.00 15 o10.0o) a63① (.00) a.00) (0.00) (0.C0) 0.13 (0.62) (1.01) a17⊙ 001 p.16 0.16⊙ 0.07 0.07 .00 a5s⊙ 0.98 (.17) (0.01) 0.16) (0.15) (0.05) ⊙ 003) (0.10) (a62 (0.93) 8 ⑧ 日 0.76 30.29 1.81Yc.00 0.00 0.10 .0 o.o0 0.09 0.87) (0.39 (1.711.10.07) 〔0.05) (0.14) 0.03) (0.19) (0.65) (a) 可,分布图 () ,分布因 )r,升布西 注:搭号()内的值为有限元结果 田1,4自重应力分布因 、 因1.5 10