聊城大学：《拓扑学 Topology》课程教学资源（PPT课件讲稿）第二章 度量空间与连续映射 2.6 基与于基

第六节基与于基

定义2.6.1设(X,T)是一个拓扑空 间，B是T的一个子族.如果T中的 每一个元素（即拓扑空间X中的每一个 开集)是B中某些元素的并，即对于每 一个U∈T,存在B,cB使得 U=UB B∈B1 则称B是拓扑T的一个基，或称B是 拓扑空间X的一个基

B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基． B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基． B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基． B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基． B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基． B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基． B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基． B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基． B B 1  B B 1 U B  = 定义2.6.1 设(X, T)是一个拓扑空 间，B 是 T 的一个子族．如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并，即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基，或称B 是 拓扑空间 X 的一个基．

定理2.6.1一个度量空间中的 所有球形邻域构成的集族是这个度 量空间作为拓扑空间时的一个基. 注：(1)实数空间R中所有的开区间 构成的集族是它的一个基。 (2)离散空间中所有单点集构成 的族是它的一个基

定理2.6.1 一个度量空间中的 所有球形邻域构成的集族是这个度 量空间作为拓扑空间时的一个基． 注:(1)实数空间 R 中所有的开区间 构成的集族是它的一个基. (2)离散空间中所有单点集构成 的族是它的一个基

问 题 ◆任何一个拓空间是否都存在基？ ◆拓扑空间的基是否夺一？

问 题 ◆任何一个拓扑空间是否都存在基？ ◆拓扑空间的基是否存一？

定理2.6.2 设B是拓扑空间 (X,T)的一个开集族，则B是拓扑 空间X的一个基当且仅当对于每一 个x∈X和x的每一个邻域U, 存在V∈B使得x∈VCU

Ux Vx B x x x V U   定 理2.6.2 设 B 是拓扑空间 (X，T)的一个开集族,则 B 是拓扑 空间 X 的一个基当且仅当对于每一 个 x∈X 和 x 的每一个邻域 ， 存在 使得 . Ux Vx B x x x V U   定 理2.6.2 设 B 是拓扑空间 (X，T)的一个开集族,则 B 是拓扑 空间 X 的一个基当且仅当对于每一 个 x∈X 和 x 的每一个邻域 ， 存在 使得 . Ux Vx B x x x V U   定 理2.6.2 设 B 是拓扑空间 (X，T)的一个开集族,则 B 是拓扑 空间 X 的一个基当且仅当对于每一 个 x∈X 和 x 的每一个邻域 ， 存在 使得 . Ux Vx B x x x V U   定理2.6.2 设 B 是拓扑空间 (X，T)的一个开集族,则 B 是拓扑 空间 X 的一个基当且仅当对于每一 个 x∈X 和 x 的每一个邻域 ， 存在 使得

证明：必要性：如果B是X的 一个基，则对于每一个x∈X和x的 每一个邻域U,存在x的一个开邻 域W,使得x∈WcUx.由于W 是一个开集，根据基的定义，存在 B,cB,使得W=UA.故存在 A∈B1 V,∈B,cB使得 x∈VCUA=W,cU, A∈B1

证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    =  证明：必要性：如果 B 是 X 的 一个基，则对于每一个 x∈X 和 x 的 每一个邻域 ，存在 x 的一个开邻 域 使得 .由于 是—个开集，根据基的定义，存在 ，使得 ．故存在 使得 Ux Wx x x x W U   Wx B B 1  B 1 x A W A  = Vx   B B 1 B 1 x x x A x V A W U    = 

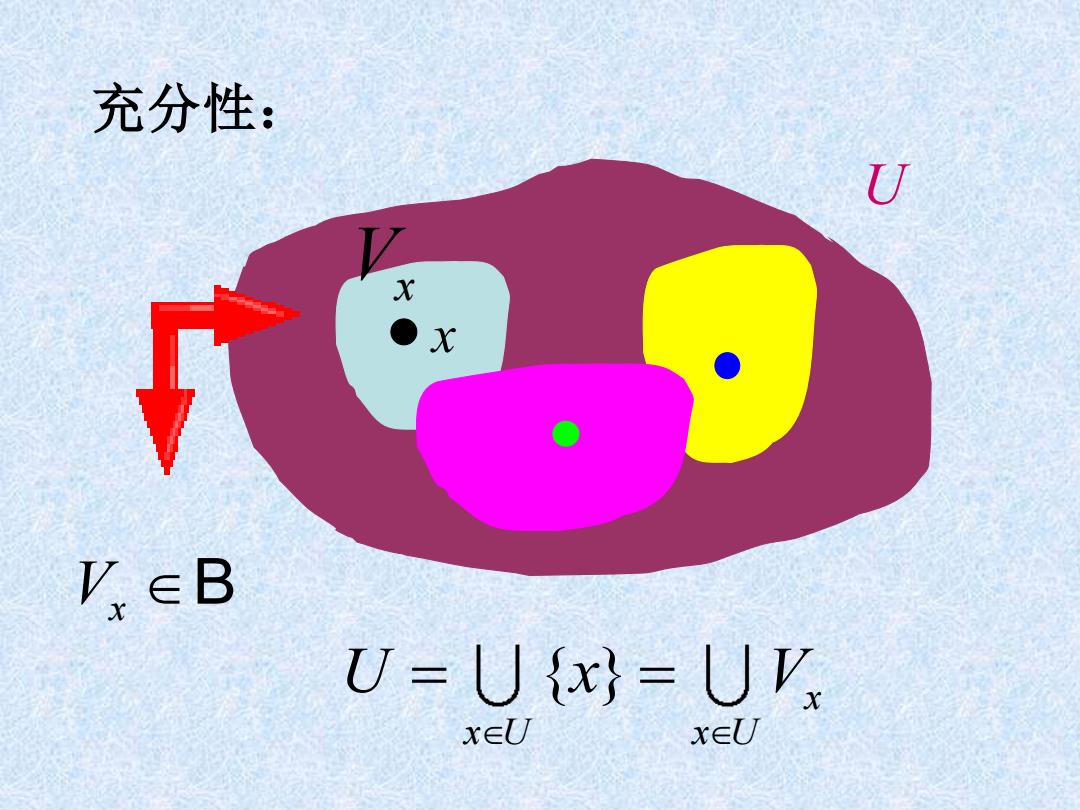
充分性： U X ●x y∈B U=Ux=UK x∈UJ x∈LU

充分性： U x Vx Vx B { } x x U x U U x V   = =

充分性：如果是X中的任意开 集，则对于每一个x∈U,由于U是x 的一个邻域，故存在V∈B,使得 x∈VcU.于是 U=UxEUK.cU x∈UU x∈LU 因此U=UV,,故U是B中某些 XEU 元素之并，从而B是X的一个基

充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  = 充分性：如果 U 是 X 中的任意开 集，则对于每一个 x∈U,由于U 是 x 的一个邻域，故存在 ，使得 . 于是 因此 ，故 U 是 B 中某些 元素之并，从而 B 是 X 的一个基. x x V U   Vx B { } x x U x U U x V U   =   x x U U V  =

定理2.6.3设X是一个集合，B 是集合X的一个子集族.如果B满 足条件： (1)UBeB B=X (2)如果B,B2∈B,则对于任何 x∈B∩B2,存在B∈B使得 x∈BCB,∩B2

定理2.6.3 设 X 是一个集合，B 是集合 X 的一个子集族．如果 B 满 足条件： (1) ； (2) 如果 ，则对于任何 ，存在 使得 . BB B X = 1 2 B B, B 1 2 x B B   BB 1 2 x B B B    定理2.6.3 设 X 是一个集合，B 是集合 X 的一个子集族．如果 B 满 足条件： (1) ； (2) 如果 ，则对于任何 ，存在 使得 . BB B X = 1 2 B B, B 1 2 x B B   BB 1 2 x B B B    定理2.6.3 设 X 是一个集合，B 是集合 X 的一个子集族．如果 B 满 足条件： (1) ； (2) 如果 ，则对于任何 ，存在 使得 . BB B X = 1 2 B B, B 1 2 x B B   BB 1 2 x B B B   

则X的子集族 T=UCX|存在BucB使得U=UB} BeB U 是集合X的唯一的一个以B为基 的拓扑； 反之，如果X的一个子集族B是X 的某一个拓扑的基，则B一定满足 条件(1)和(2)：

{U X | 存在 使得U B} B U T B U B B   =   = 则 X 的子集族 是集合 X 的唯一的一个以 B 为基 的拓扑； 反之，如果 X 的一个子集族B是 X 的某一个拓扑的基，则B一定满足 条件(1)和(2). {U X | 存在 使得U B} B U T B U B B   =   = 则 X 的子集族 是集合 X 的唯一的一个以 B 为基 的拓扑； 反之，如果 X 的一个子集族B是 X 的某一个拓扑的基，则B一定满足 条件(1)和(2)