
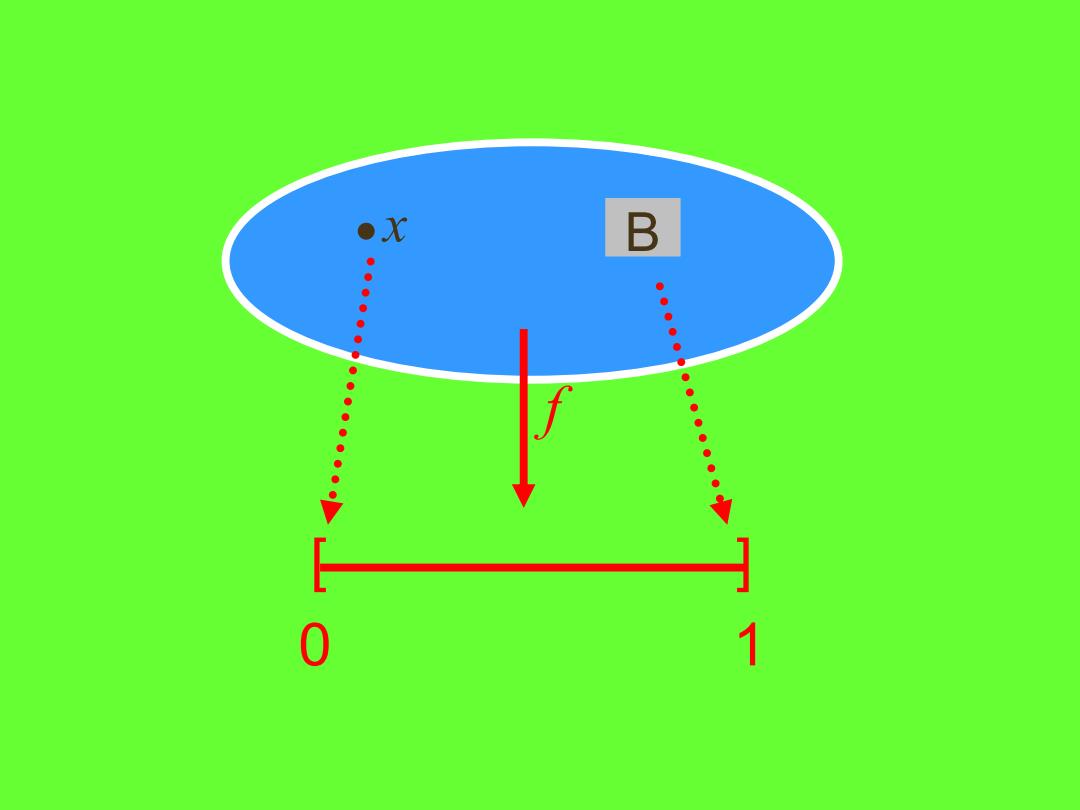
§6.4完全正则空间,Tychonoff空间 定义6.4.1 设X是一个拓扑空问.如 果对于任意x∈X和X中任何一个不包含 点x的闭集B存在一个连续映射∫:X→[0,1] 使得fx)=0 以及对于任何y∈B有f(y)=1, 则称拓扑空间x是一个完全正则空间 完全正则的T,空间称为Tychonoff:空间或T3s空间
§6.4 完全正则空间,Tychonoff空间 定义6.4.1 设X是一个拓扑空问.如 果对于任意 和X中任何一个不包含 点x的闭集B存在一个连续映射 使得 以及对于任何 有 , 则称拓扑空间X是一个 . x X f X: [0,1] → f x( ) 0 = y B f y( ) 1 = 完全正则的T1空间称为Tychonoff空间或T3.5空间

定理6.4.1每一个完全正则空间都 是正则空间 证明:对于任意x和不包含x的闭集B, 由于X是一个完全正则空间,故对x和闭集 B存在一个连续映射 f:X>[0,1] 使得对于x和不包含x的闭集B有x)=0 及任意y∈B有f(y)=1
定理6.4.1 每一个完全正则空间都 是正则空间. 证明:对于任意x和不包含x的闭集B, 由于X是一个完全正则空间,故对x和闭集 B存在一个连续映射 , 使得对于x和不包含x的闭集B有 及任意 有 . f X: [0,1] → f x( ) 0 = y B f y( ) 1 =
ox B 0 1
0 1 [ ( ] 23 x B f V

注:每个Tychonoff2空间都是T3空间 每一个T空间都是Tychonoff?空间 定理6.4.2每一个正则且正规的 空间都是完全正则空间:
注:每个Tychonoff空间都是T3空间 每一个T4空间都是Tychonoff空间 定理6.4.2 每 一个正则且正规的 空间都是完全正则空间
X B 0 1
0 1 [ ] x B f

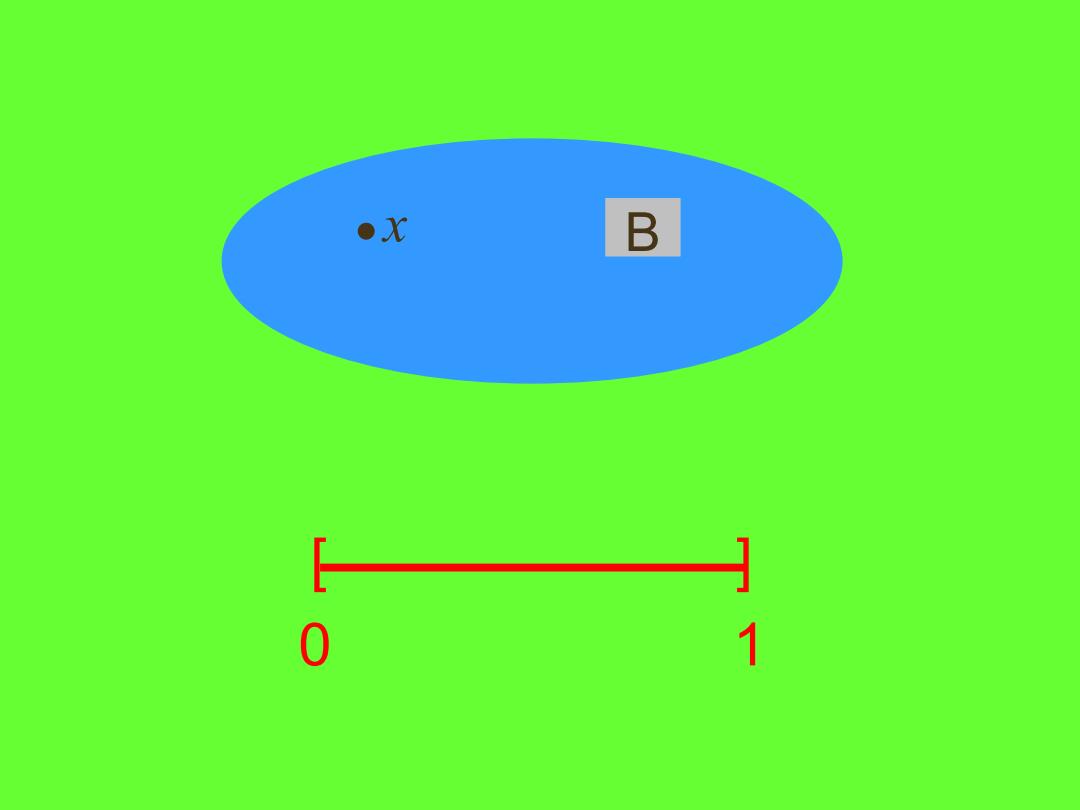
证硼设X是一个既正则又正规的空间,设x∈X,B是X 中的-个不包含点x的闭集由于X是一个正则空间,根据定理 6.2.1,点x有-个开邻域U使得UCB.令A=U则A和B是 X中无交的两个闭集.由于X是一个正规空间,应用Urysohn引 理可见,存在-个连续映射f:X→[0,1]使得对于任何yA有 fy)=0和对于任何yEB有f代y=1,由于x∈A,放fz)=1, 这就证明了X是一个完全正则空间.·

定理6.4.3每一个正则的Lindeloff 空间都是正规空间
定理6.4.3 每一个正则的Lindelöff 空间都是正规空间

A B X·
A B x

证明设X是-个正则的空间设A和B是X中 的辆个无交的闭集时杆-个长从,由于:B,限定理 621可见,存在:的-个开U使得U:CB,即U:B= 集族U,A是ǖ集A的-个开覆盖由于孔n的f空萌

的每-个闭子空间都是Lindelof空间(参见定理5,3.4),见A 的开覆盖儿,xA中有-个可数子族,设为U4,然覆 盖A注意:对于每-个忍+,有UB=0.同理,集台B也 有-个可数开覆盖1:,使得对于任狗正3,有八A: