
第大章分离性公理 §6.1To,Ti,Hausdorff?间 §6.4完全正则空间,T空间 §6.2正则,正规,T3,T4空间 §6.5分离性公理与子空间 §6.3引理和T-扩张定理 §6.6可度量化空间
§6.1 T0 ,T1 ,Hausdorff空间 §6.2 正则,正规,T3 ,T4空间 §6.3 U-引理和T-扩张定理 §6.4 完全正则空间,T-空间 §6.5 分离性公理与子空间 §6.6 可度量化空间

§6.1To,T,Hausdorff:空间 定义6.1.1X是一个拓扑 空间,如果对于X中任意两个不 同的点中必有一个点有一个开 邻域不包含另一点,则称拓扑空 间X是一个To空间
§6.1 T0 ,T1 ,Hausdorff空间 定义 6.1.1 X 是一个拓扑 空间, 如果对于X中任意两个不 同的点中必有一个点有一个开 邻域不包含另 一点,则称拓扑空 间X 是一个T0空间
U 文 y 少廷乙I To 空 间
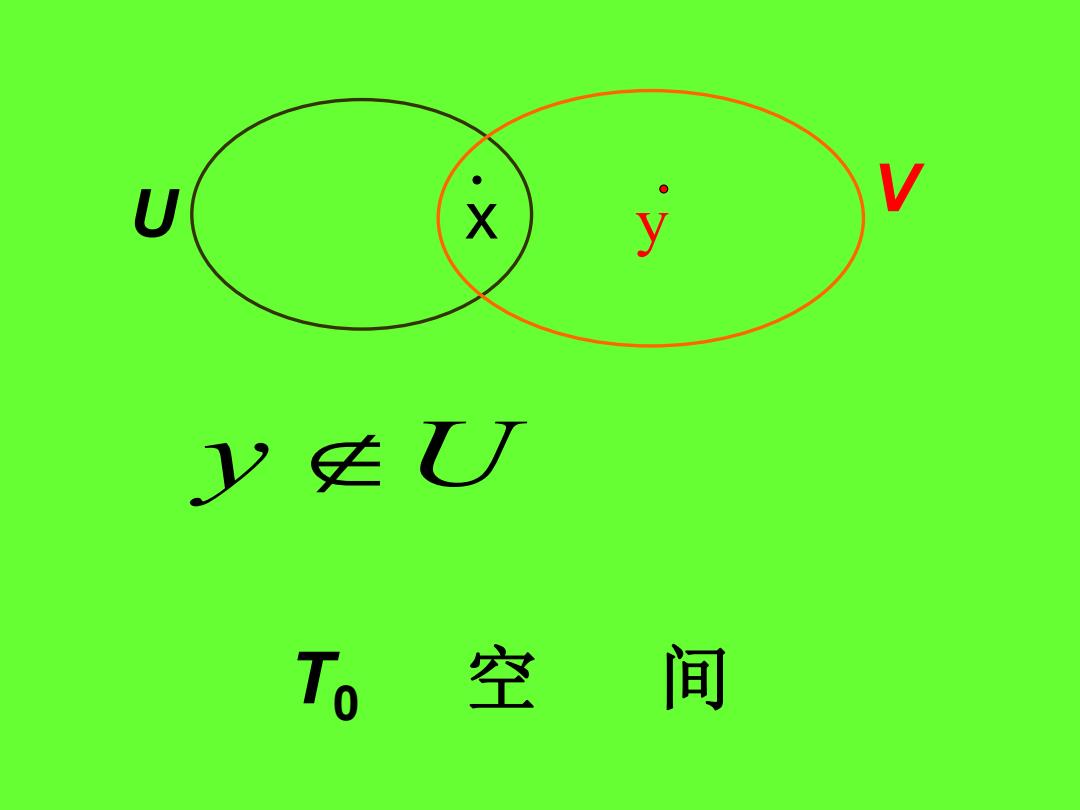
U x y V T0 空 间 y U

定理6.1.1拓扑空间X 是一个T,空间当且仅当X中 任意两个不同的单点集有不 同的闭包 即若≠y,则 x≠y
定理6.1.1 拓扑空间X 是一个T0空间当且仅当X中 任意两个不同的单点集有不 同的闭包. 即若x≠y,则 { } { } x y

证明:充分性「 因为对于任意的 x,y∈X,有 x≠y网 从而必有: {x}-{y≠ or {y-{x}≠p 若 {x}-{y以≠中, 必有x{以 ,故 x∈x-;同理可证当-女 时,y∈X-{x,因此X是一个T空间
证明:充分性 因为对于任意的 x,y∈X,有 ,从而必有: or . 若 ,必有 ,故 ;同理可证当 时, ,因此X是一个T0空间. { } { } x y { } { } x y − { } { } y x − { } { } x y − x y { } x X y −{ } { } { } y x − y X x −{ }

必要性设X是一个T,空间,则对 任意X,y∈X≠y,则或者有x的开邻域 U使得yU,或者有y的开邻域V,使 得x先V ,对于前一种情形,由于 U个y三中,从而xy 于是x≠y;同理若是后一种情形, 也有 {x}夫{y
必要性 设X是一个T0空间,则对 任意x,y∈X,x≠y,则或者有x的开邻域 U使得 ,或者有y的开邻域V,使 得 ,对于前一种情形,由于 , 从而 , 于是 ;同理若是后一种情形, 也有 . y U x V U y = { } x y { } { } { } x y { } { } x y

定义6.1.2 X是一个拓扑空间 若X中任意两个不相同的点都有一 个开邻域不包含另一点,则称拓 扑空间X是一个T空间
定义6.1.2 X 是一个拓扑空间, 若X中任意两个不相同的点都有一 个开邻域不包含另一点,则称拓 扑空间X是一个T1空间

x主Vy主UU T1空间
U x y V x V y U T1 空 间

注:T,空间当然是T空间 T。空间不是T空间的例子 例:X=0,1) T={D,X,{O}
T0空间不是T1空间的例子 注:T1空间当然是T0空间 例: , T = X ={0,1} { , ,{0}} X

定理6.1.2 设X是一个拓扑空 间,则下列条件等价: (1)X是一个T空间: (2)X中每一个单点集都是闭集; (3)X中每一个有限子集都是闭集 Next th
定理6.1.2 设X是一个拓扑空 间,则下列条件等价: (1)X是一个T1空间; (2)X中每一个单点集都是闭集; (3)X中每一个有限子集都是闭集. Next th