
P成水学 情品课程 LIAOCHENG UNIVERSITY 第六节局部紧致空间,仿紧性空间 厚德博学笃志精算 在这一节中,我们对紧致性空间这个概念从两方面加以 推广:一是推广为局部紧致空间,另一是推广为仿紧致空间. 研究的结果表明,这两者都在很大程度上保持着紧致空间的 特色 求实务实 踏实 扎实
第六节 局部紧致空间,仿紧性空间 在这一节中,我们对紧致性空间这个概念从两方面加以 推广:一是推广为局部紧致空间,另一是推广为仿紧致空间. 研究的结果表明,这两者都在很大程度上保持着紧致空间的 特色

P放大学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 定义7.6.1设X是一个拓扑空间.如果X中的每一个点都 有一个紧致的邻域,则称拓扑空间X是一个局部紧致空间: 定理7.6.1每一个局部紧致的Hausdorff空间都是正则空间. 求实务实 踏实 扎实
定 义 7.6.1 设 X 是一个拓扑空间.如 果 X 中的每一个点都 有一个紧致的邻域,则称拓扑空间 X 是一个局部紧致空间. 定理 7.6.1 每一个局部紧致的 Hausdorff 空间都是正则空间

P成术学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 定理7.6.2设X是一个局部紧致的正则空间,x∈X.则点x 的所有紧致邻域构成的集族是拓扑空间X在点x处的一个邻域基, 推论7.6.3设X是一个局部紧致的Hausdorff空间,x∈X. 则点x的所有紧致邻域构成的集族是拓扑空间X在点x处的一个邻 域基 定理7.6.4每一个局部紧致的正则空间都是完全正则空间. 求实务实 踏实扎实
定 理 7.6.2 设 X 是一个局部紧致的正则空间, x X .则点x 的所有紧致邻域构成的集族是拓扑空间 X 在点 x 处的一个邻域基. 推论 7.6.3 设 X 是一个局部紧致的Hausdorff空间, x X . 则点 x的所有紧致邻域构成的集族是拓扑空间 X 在点x 处的一个邻 域基. 定理 7.6.4 每一个局部紧致的正则空间都是完全正则空间

P成术学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 定义7.62 设集族A和B都是集合X的覆盖.如果A中的每一个元 素包含于B的某一个元素之中,则称A是B的一个加细. 显然,如果A是B的一个子覆盖,则A是B的一个加细 定义7.6.3设X是一个拓扑空间,A是X的子集A的一个覆盖.如果 对于每一个x∈A,点x有一个邻域仅与A中有限个元素有非空的交,即 {A∈AA∩U≠O 是一个有限集,则称A是集合A的一个局部有限覆盖 求实务实 踏实扎实
定义 7.6.2 设集族 和 都是集合 X 的覆盖.如果 中的每一个元 素包含于 的某一个元素之中,则称 是 的一个加细. 显然,如果 是 的一个子覆盖,则 是 的一个加细. 定义 7.6.3 设 X 是一个拓扑空间, 是 X 的子集 A 的一个覆盖.如果 对于每一个 x A ,点 x 有一个邻域仅与 中有限个元素有非空的交,即 { } A A U 是一个有限集,则 称 是集合 A 的一个局部有限覆盖

P议衣学 精品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 有限覆盖当然是局部有限的覆盖。 例如,在实数空间R中令 A={(n-1,n+1)n∈Z} B={(-n,nm)ln∈Z} 则A和B都是R的开覆盖,并且A是B的一个加细,而B却不是A的 加细.此外A是一个局部有限的覆盖,然而B却不是局部有限的. 求实务实 踏实扎实
有限覆盖当然是局部有限的覆盖. 例如,在实数空间 R 中 令 = − + {( 1, 1) | } n n n Z = − {( , ) | } n n n Z+ 则 和 都 是 R 的开覆盖,并且 是 的一个加细,而 却不是 的 加细.此外 是一个局部有限的覆盖,然而 却不是局部有限的
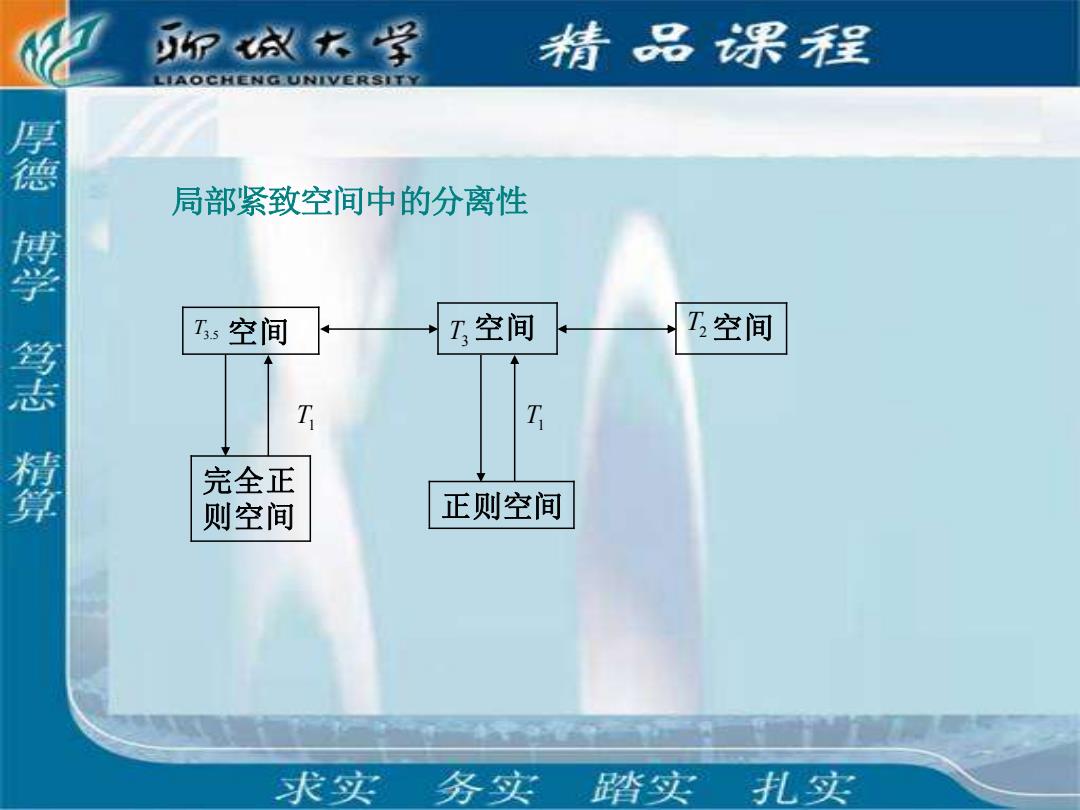
P成衣学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 局部紧致空间中的分离性 Is空间 1,空间 T空间 T T 完全正 则空间 正则空间 求实务实 踏实 扎实
空间 空间 局部紧致空间中的分离性 T3.5 T1 T3 空间 完全正 则空间 正则空间 T1 T2

P成衣学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 定义7.6.4设X是一个拓扑空间.如果X的每一个开覆盖都有一个局 部有限的开覆盖是它的加细,则称拓扑空间X是一个仿紧致空间。 例如,紧致空间自然是仿紧致的,离散空间也是仿紧致的,因为所有单点集 构成的集族是离散空间的一个开覆盖并且它的任何一个开覆盖的局部有限的 加细。 定理7.6.5每一个仿紧致的正则空间都是正规空间. 定理7.6.6每一个仿紧致的Hausdorff空间都是正则空间,因而也 是正规空间 求实务实 踏实扎实
定 义 7.6.4 设 X 是一个拓扑空间.如果 X 的每一个开覆盖都有一个局 部有限的开覆盖是它的加细,则称拓扑空间 X 是一个仿紧致空间. 例如,紧致空间自然是仿紧致的,离散空间也是仿紧致的,因为所有单点集 构成的集族是离散空间的一个开覆盖并且它的任何一个开覆盖的局部有限的 加细. 定理 7.6.5 每一个仿紧致的正则空间都是正规空间. 定理 7.6.6 每一个仿紧致的 Hausdorff 空间都是正则空间,因而也 是正规空间
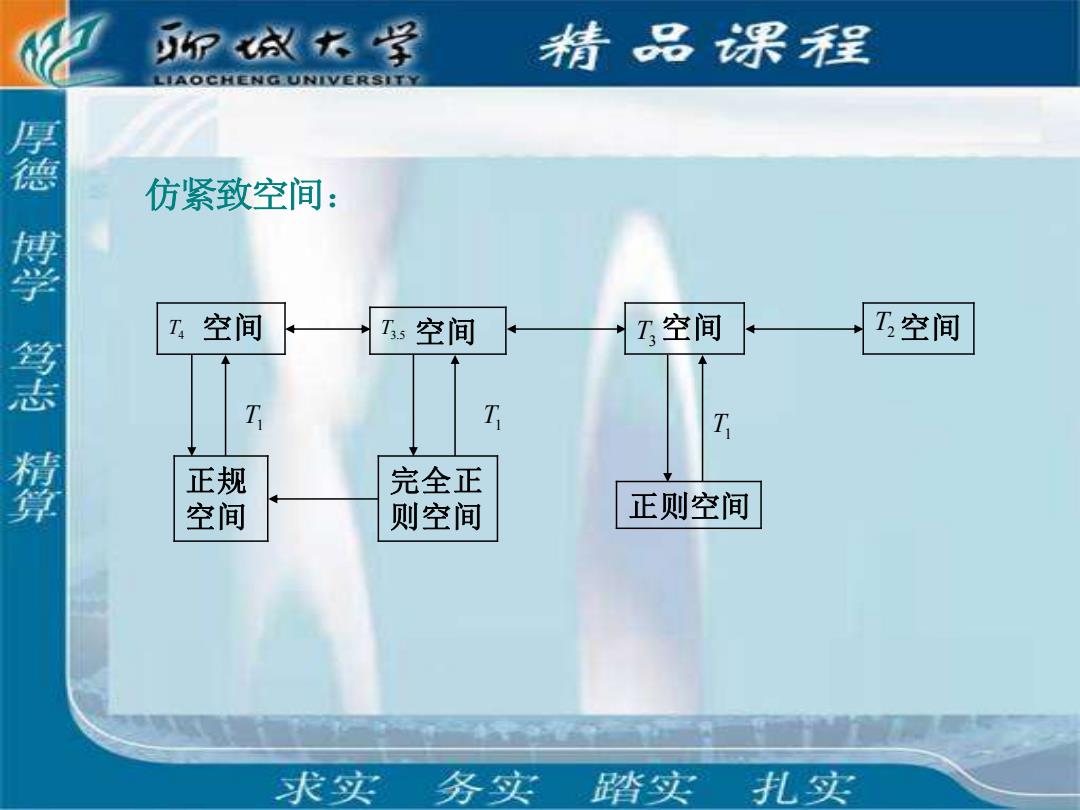
P成衣学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 仿紧致空间: 1空间 I:空间 工,空间 T,空间 T T T 正规 完全正 空间 则空间 正则空间 求实务实 踏实扎实
空间 空间 空间 仿紧致空间: T4 T3.5 T1 T3 空间 正规 空间 完全正 则空间 正则空间 T1 T1 T2

P成术学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 引理7.6.7设X是一个满足第二可数性公理的局部紧致的Hausdorff 空间.则X有一个开覆盖{,,}满足条件:对于每一个i∈Z,闭包 是一个包含于V的紧致子集 定理7.6.8每一个满足第二可数性公理的局部紧致的Hausdor ff 空间都是仿紧致空间. 求实务实 踏实扎实
引理 7.6.7 设 X 是一个满足第二可数性公理的局部紧致的 Hausdorff 空 间.则 X 有一个开覆盖 1 2 { , , } V V 满足条件:对于每一个i Z + ,闭 包Vi − 是一个包含于 Vi+1 的紧致子集. 定理 7.6.8 每一个满足第二可数性公理的局部紧致的 Hausdorff 空间都是仿紧致空间

P放大学 情品课程 LIAOCHENG UNIVERSITY 厚德博学笃志精算 紧性、局部紧性、局部紧致空间 仿紧致空 紧致空间 局部紧致空间 间 T和A 求实务实 踏实扎实
紧性、局部紧性、局部紧致空间 仿紧致空 间 紧致空间 局部紧致空间 T2 和 A 2