
2021-12-28 《数学建模》课件汇总 一。学习理念探究 数学建模 普林新顿大业 普林斯顿大学本科生12来培养目标: 何国良 (1)具有清楚地思维、谈吐、写作的能力: (2)具有以批评的方式系航地推理的能力: 电子科技大学 (3)具有形成概念和解决问题的能力: 数学科学学院 (4)具有独立思考的能力: 数学建摸山2 数学座摸23 (5)具有敢于创新及独立工作的能力; 盖妻阳客: (6)具有与他人合作的能力: 欧学习一些知机、 (9)熟悉不同的思维方式: 坡她的外: (10)具有某一领域知识的深度: (11)具有观察不同学科、文化、理念相 更重要 关之处的能力; (12)终身学习能力 创造力的初步形成,及与之匹配的 创新精神、创新意识、创新能力. 数学建模32压 数学建模23 二课程教学目标 教学方式 裸程性质 采用问题驱动式教学方式训练学生学会如 工程教育与实践创新 何思考,如何分析,如何用不同的角度和不 同的方法去看待数学问题,体会如何从各类 原则 现实问题抽象出数学结构及其描述。 培养工程素养,帮助学生从人文、 考核方式 社会、经济、管理等多视角扩展工程 实践领域,提高工程设计开发、创新 平时练习题(20%)+半期(20%)+期末 实践与团队协作能力等. 考试(60%) 敢学逸模5 数学速模2 第1页,共105页
2021-12-28 数学建模 1/23 电子科技大学 数学科学学院 何国良 数学建模 2/23 一. 学习理念探究 普林斯顿大学 普林斯顿大学本科生12条培养目标: (1)具有清楚地思维、谈吐、写作的能力; (2)具有以批评的方式系统地推理的能力; (3)具有形成概念和解决问题的能力; (4)具有独立思考的能力; 数学建模 3/23 (5)具有敢于创新及独立工作的能力; (6)具有与他人合作的能力; (9)熟悉不同的思维方式; (10)具有某一领域知识的深度; (11)具有观察不同学科、文化、理念相 关之处的能力; (12)终身学习能力. 数学建模 4/23 更重要 创造力的初步形成,及与之匹配的 创新精神、创新意识、创新能力. 主要内容: 除学习一些知识、 技能的外; 数学建模 5/23 课程性质 工程教育与实践创新 原则 培养工程素养,帮助学生从人文、 社会、经济、管理等多视角扩展工程 实践领域,提高工程设计开发、创新 实践与团队协作能力等. 二.课程教学目标 数学建模 6/23 教学方式 平时练习题(20%)+半期(20%)+ 期末 考试(60%) 采用问题驱动式教学方式训练学生学会如 何思考,如何分析, 如何用不同的角度和不 同的方法去看待数学问题,体会如何从各类 现实问题抽象出数学结构及其描述。 考核方式 《数学建模》课件汇总 第1页,共105页
2021-12-28 《数学建模》课件汇总 第一章序言 21世纪科技人才应具备的数学素质与能力 一数学科学的重要性 亚 现代数学:在理论上更抽象; 在方法上更加综合 在应用上更为广泛。 抽象思维能力 逻辑推理能力 数学运算能力 空间想象能力 数学建模能力 数据处理能力 使用数学软件能力 更新数学知识能力 数学建摸 123 数学难襲 8/23 数学建模案例 一七桥问题 数学建模923 1023 如何解决? 问题 有设有一次准 这七座 又回到起点的 方呢 一笔画问题 敦学建模1西 数学建模22四 第2页,共105页
2021-12-28 数学建模 7/23 一. 数学科学的重要性 第一章 序言 现代数学: 在理论上更抽象; 在方法上更加综合; 在应用上更为广泛。 数学建模 8/23 21世纪科技人才应具备的数学素质与能力 数 学 运 算 能 力 逻 辑 推 理 能 力 数 学 建 模 能 力 数 据 处 理 能 力 空 间 想 象 能 力 抽 象 思 维 能 力 更 新 数 学 知 识 能 力 使 用 数 学 软 件 能 力 数学建模 9/23 数学建模案例 —七桥问题 数学建模 10/23 数学建模 11/23 有没有一次性 走遍这七座桥 又回到起点的 方案呢? 数学建模 12/23 一笔画问题 如何解决? 《数学建模》课件汇总 第2页,共105页

2021-12-28 《数学建模》课件汇总 如何解决? 如何解决? 结论: 若要有回路 所有点为偶 “度 和点相连的边的 度数点! 数学建摸132s 数学壁摸 升华 二数学模型与数学建模 欧拉开创了图 数学模型(E.A.Bendar定义):关于部分现失世界 论与拓扑 为一定目的而做的抽象、筒化的数学结构。 ●数学模型是现实世界的简化而本质的精述。 ·建立数学模型的过租需 要假设。 ·用数学符号、敦学公 式、程序、图、表等 刘画客观事物的本质 属性与内在联系的理 想化表述。 数学建模1523 数学建模1623 例2.生物医学专家有了药物浓度在人体内随时 二数学模型与数学建模 间和空间变化的数学模型后,可以用来分析药 物的疗效,从而有效地指导临床用药。 数学建模指创立一个数学模型的全过程。 例3.厂长经理们筹划出一个合理安排生产和销 是运用数学的思雄方法、数学 售的数学模型,是为了获取尽可能高的经济效 的语言去近似地刘岛实际问题, 并加以解决的全过租。 益。 数学建模:创立一个数学模型的全过程 是运用数学的思维方法、数学的语言去近似 地刻画实际问题,并加以解决的全过程。 敦学建模1四 数学速模182四 第3页,共105页
2021-12-28 数学建模 13/23 “度” 和点相连的边的 条数为偶数! 如何解决? 数学建模 14/23 结论: 如何解决? 数学建模 15/23 Te xt he re! 问题 分析 图形 抽象 一笔画 数点 度数 进一 步研 究 欧拉开创了 与 升华 数学建模 16/23 数学模型(E.A.Bendar 定义):关于部分现实世界 为一定目的而做的抽象、简化的数学结构。 l 数学模型是现实世界的简化而本质的描述。 l 用数学符号、数学公 式、程序、图、表等 刻画客观事物的本质 属性与内在联系的理 想化表述。 二. 数学模型与数学建模 l 建立数学模型的过程需 要假设。 数学建模 17/23 数学建模指创立一个数学模型的全过程。 是运用数学的思维方法、数学 的语言去近似地刻画实际问题, 并加以解决的全过程。 二. 数学模型与数学建模 数学建模 18/23 生物医学专家有了药物浓度在人体内随时 间和空间变化的数学模型后,可以用来分析药 物的疗效,从而有效地指导临床用药。 厂长经理们筹划出一个合理安排生产和销 售的数学模型,是为了获取尽可能高的经济效 益。 数学建模:创立一个数学模型的全过程 是运用数学的思维方法、数学的语言去近似 地刻画实际问题,并加以解决的全过程。 《数学建模》课件汇总 第3页,共105页

2021-12-28 《数学建模》课件汇总 三数学建模的教与学 应用数学的过程的五个阶段: 学习数学建模的困难: 1.科学地识别和剖析问题; ()“学着用”数学和“学”数学根本不同 在于明白在何处用数学,怎样用数学: 2.建立数学模型; 3.对研究中所选择的模型求解数学问题; (2)掌握成功运用数学建立数学模型所需的 技能与理解数学概念、证明定理、求解方程所 4.对有关计算提出算法和设计计算机程序: 需的技巧迥然不同。 5。解释原问题的结论并评判这些结论。 建立数学模数是购用数学的关健山重要的一步, 如何解决? 数学建摸19 数学座摸 2023 建议: 三个学会 去做!去实践! 学着用,干中学! 学会理解 学会表达 理解数学知识的基础上,重点是数学 方法的掌握、数学思维的建立。 学会思考 数学建模23 数学建模223 参考文献 [山]姜启源谢金里,叶俊,数学模型(第三版),高等教育 出版社,1999. 2]Frank R等,数学建模(第s版),机械工业出版 杜2017. [3王沫然,Matlab6.0与科学计算,电子工业出版 社,2001. 【4」司守奎、孙兆亮,数学建模算法与应用(第5 版),国防工业出版社,2017. 敦学建模232四 第4页,共105页
2021-12-28 数学建模 19/23 三. 数学建模的教与学 应用数学的过程的五个阶段: 1. 科学地识别和剖析问题; 2. 建立数学模型; 3. 对研究中所选择的模型求解数学问题; 4. 对有关计算提出算法和设计计算机程序; 5. 解释原问题的结论并评判这些结论。 数学建模 20/23 学习数学建模的困难: (1) “学着用”数学和“学”数学根本不同 在于明白在何处用数学,怎样用数学; (2) 掌握成功运用数学建立数学模型所需的 技能与理解数学概念、证明定理、求解方程所 需的技巧迥然不同。 如何解决? 数学建模 21/23 建议: 去做!去实践! 学着用,干中学! 理解数学知识的基础上,重点是数学 方法的掌握、数学思维的建立。 数学建模 22/23 三个学会 数学建模 23/23 姜启源,谢金星,叶俊, 数学模型(第三版), 高等教育 出版社,1999. [2] Frank R等, 数学建模(第5版),机械工业出版 社,2017. [3] 王沫然, Matlab6.0与科学计算, 电子工业出版 社,2001. [4] 司守奎、孙兆亮,数学建模算法与应用(第5 版),国防工业出版社,2017. 参考文献 《数学建模》课件汇总 第4页,共105页
2021-12-28 《数学建模》课件汇总 海 数学建模简介 数学建模题日特点 与传统鼓学题目的区别 没有严格的泰件 没有唯一标准答策 URE8E n34. 标准案 n5声如-5)- 简介 去王没有数福 一数学建模简介 教学建模基本步霖 数学建模是创断 数学建模过框是一种创新过准,在思考方法和思 实标问题分析 建立数学模型 雄方式上与其他数学课程有枝大差别。 重要的科学思维方式之一是创新 提交论文与报告 求解敦学棋型 思维, 创新思维是创新能力的 核心与灵魂。 棋型解的分析及检验 作业1 一.数学模型的地位和意义 数学根型是失际问画的模拟葡化,是对实际问题的近似表 观察白已的学习、生活,从周国寻找一个可能的可 示,它的完成是在某种合理的银设下光成的。 以用数学去量化描述的事、物。 建提体果其只能是较忧的 不是赠一的。竟赛的成采一般 忌考: 是论文, 怎么和数学有关,怎么量化? 数学建模壳養偏重于应用, 下次课的时候请三位同学来分享。 它以数学如识为引导,计與机 应用能力及文章的写作能力为 辅的综合能力竟赛, 第5页,共105页 1
2021-12-28 1 1 简介 与传统数学题目的区别 没有严格的条件 没有唯一标准答案 甚至没有数据 一. 数学建模简介 求解数学模型 实际问题分析 建立数学模型 模型解的分析及检验 提交论文与报告 一. 数学建模简介 数学建模过程是一种 创新过程,在思考方法和思 维方式上与其他数学课程有较大差别 . 重要的科学思维方式之一是创新 思维 , 创新思维是创新能力的 核心与灵魂 . 作业1 观察自己的学习、生活,从周围寻找一个 可能的可 以用数学去量化描述的事、物 。 思考: 怎么和数学有关, 怎么量化? 下次课的时候请三位同学来分享。 6 数学模型是实际问题的模拟简化,是对实际问题的近似表 示,它的完成是在某种合理的假设下完成的。 建模结果其只能是 较优的, 不是唯一的。竞赛的成果一般 是论文。 一. 数学模型的地位和意义 数学建模竞赛偏重于 应用, 它以数学知识为引导, 计算机 应用能力及文章的写作能力为 辅的综合能力竞赛。 《数学建模》课件汇总 第5页,共105页

2021-12-28 《数学建模》课件汇总 二·数学建模的主要作用 二.数学建模的主要作 很多学生用一就水享,岸十且, 学将金我.日 来描述他们的参赛感受。许多参加过 快速学日 竟赛的同学的·《鲁前和青可加力显 培养能 菁提高,在单业设计和研究生阶段的 力 表现出明显的优势,得到用人草位和 研究生导师的普遍认可。 数学建模在里现知识与战能 的周时,童视季生已有的经验, 3 使季生体险从失际背景中袖康 雨飘体作 表达力 出数季问题,种建教季模型, 音体果、尊使问题的过狂。 三,中国大学生数学建模竟赛简介: 三、中国大学生数学建模竞赛简价: 在国内一般也林“金国大学生数学建模竞赛”。 从1992年开始,毒年一属,分为本解姐和 专料加。 竟熹以三个人本科生(专科)为一如,利 用三天,从ABCD四个题目中选枰一个来完 教 成(本科生从AB两题中选杯一题宽成,青科 生从CD两题中进择一题来完成)。 中国工业与应用数学学会 它是国前面向企国高普院校的一项规模最大的学生课外科技 部 活动。 全图大学生数学建模竟春是由散宵等高警食育即与中口工 2018年,来自全图33个嘴/市/区(包括青港、溴门和合湾)及美 意幅点用意学◆冷共月華办的。 国和新加城的1449所院校/校区、42128个队(本升38573队、专 科3555队)、超过12万名大季生报名◆加本项竟喜。 r■ 三中国大学生数学建模竞赛简介: 四、美国大学生数学建模竞赛简介: 比赛时间■ 参赛日期:海年9月第二个周末 是国大季业敏学克接党察,筒善CM/CM,是一项国际拉种竟赛项调。 MM是Mathematical Contest in Modeling(敏◆淹属竟套)钟情耳,1CM是Tbe 如何要 interdisciplinary Contest in Modeling(文文学州建提党赛)的输写。MCi地于 1985年,1CM地于1999年, 由3名大学生生组成参赛队(不接受个人报名),在指定 的3天内。完成党赛。论文夏查意。 典国工业小应利学学查 复队建汉 ASA 52 COMAP 一人主管速模,一人主管偏 风四回率章单敏脚使鼻食 程,一人主管写作,合力完成 MAA 整个过程。 he 第6页,共105页 2
2021-12-28 2 2 3 1 4 5 6 培养能 力 二. 数学建模的主要作用 8 很多学生用 一次参赛,终身受益 , 来描述他们的参赛感受 。许多参加过 竞赛的同学的 自主学习 和科研能力 显 著提高,在毕业设计和研究生阶段的 表现出明显的优势,得到用人单位和 研究生导师的普遍认可。 数学建模在呈现知识与技能 的同时,重视学生已有的经验。 使学生体验从实际背景中 抽象 出数学问题, 构建数学模型, 寻求结果、解决问题的过程。 二. 数学建模的主要作用 9 三、中国大学生数学建模竞赛简介: 在国内一般也称 “全国大学生数学建模竞赛 ”。 全国大学生数学建模竞赛是由 教育部高等教育司 与中国工 业与应用数学学会 共同举办的。 10 三、中国大学生数学建模竞赛简介: 从1992年开始,每年一届,分为本科组和 专科组。 它是目前面向全国高等院校的一项规模最大的学生课外科技 活动。 竞赛以三个人本科生(专科)为一组,利 用三天,从 ABCD四个题目中选择一个来完 成(本科生从 AB两题中选择一题完成,专科 生从CD两题中选择一题来完成)。 2018年,来自全国 33个省/市/区(包括香港、澳门和台湾 )及美 国和新加坡的 1449所院校/校区、42128个队(本科 38573队、专 科3555队)、超过12万名大学生报名参加本项竞赛。 11 如何参赛 组队建议 参赛日期:每年9月第二个周末 一人主管建模,一人主管编 程,一人主管写作, 合力完成 整个过程。 由3名大学生生组成参赛队( 不接受个人报名 ),在指定 的3天内,完成竞赛。 论文要查重。 比赛时间 三、中国大学生数学建模竞赛简介: 12 四、美国大学生数学建模竞赛简介: 美国大学生数学建模竞赛,简称 MCM /ICM,是一项国际性的竞赛项目。 MCM是Mathematical Contest in Modeling (数学建模竞赛 )的缩写, ICM是The Interdisciplinary Contest in Modeling (交叉学科建模竞赛 )的缩写。 MCM始于 1985年,ICM始于1999年, The Society for Industrial and Applied Mathematics 美国工业与应用数学学会 National Council of Teachers of Mathematics 美国国家数学教师委员会 The Institute for Operations Research and the Management Sciences 运筹和管理科学学会 The American Statistical Association 美国统计协会 The Mathematical Association of America 美国数学协会 《数学建模》课件汇总 第6页,共105页

2021-12-28 《数学建模》课件汇总 四、美国大学生数学建模竟赛简介: 四、美国大学生数学建模竟赛简介: 是国数学建模竟赛评审的侧重点在于假设的合理性、建 是国大学生数学建模竞赛简介年年都吸引大量着名高校李 模的创造性、文学表达(美语)的清晰程度、关于结果的 加,近五年,毒年有提过2万个队伍参加,通及五大洲。我国 正骑性。 学生从1989年(花家大学,清单大学花末理工大学并四个 有评委强训,由于所做的假设和建立模型各不湘同,甚 队)开始参加每年的一度的MCM小CM竟赛。电子科技大学 从1992车开始参加,美国大乎生MCM/1CM竟赛,获得丁比 至差异校大,因此塘果以可能有相当大的是别,即便在特 较好的峰采。 普美的论文中莱些结果也可能相差10%,50%,善至更大。 MCM/ICM认为模型的检验越多越赶,关于模型的检验 MCM/ICM清童孩调研完问画、解决方法的原创性,国队 可以米取证明的方法。但更多的是对某些感兴鞭的情形进 合作支流以及体果的合理性。竟賽主要以三个大季生为一想, 行计算,并分新站果,对重要参数的高中低水平进行计算 在四天时间内,就指定的问题(从ABCDEF任速一个),先 成从建立提型、求解敬证到论文操写的全部工作遗晨。 份真,考感放松条件,假设条件普等。 四、美国大学生数学建模竞赛简介 四、美国大学生数学建模竟赛简介: MCM/CM主变参与国家和地区 2020年大学生竞赛获奖情况(2018年有20602队参加) ·USA, ·Mexico, 美项 所吉比例■ ·China Scotland, Outstanding 0.1% ·Canada ·Singapore, Finalist 1% ·acau S.AR ·Australia,. Meritorious 7% ·South Africa. Honorable Mention 40% ·Indonesia ·United Kingdom。 Suceessful Participant 51.9% ·Republic of Korea,. 合计 100% 四、美国大学生数学建模竞真简价: 一,数学建模简介 比赛时间 ◆享日潮:春节前后月中旬 转变 如何赛 学习思维转变 由3名大学生生组成参赛队,在指定的4天内,完成竞赛。 就短1做风1除规1 论文要查置。 普置创新风敏、用意券解决奥际问观 氢队建汉 一人主管建模,一人主管 学习态度转变 辅程,一人主管写作,合力完 婴我 成整个过程。 第7页,共105页 3
2021-12-28 3 13 美国数学建模竞赛评审的侧重点在于假设的合理性、建 模的创造性、文字表达 (英语)的清晰程度、关于结果的 正确性。 四、美国大学生数学建模竞赛简介: 有评委强调 ,由于所做的假设和建立模型各不相同,甚 至差异较大,因此结果以可能有相当大的差别,即便在特 等奖的论文中某些结果也可能相差 10%,50%,甚至更大。 MCM/ICM认为模型的检验越多越好 ,关于模型的检验 可以采取证明的方法。但更多的是对某些感兴趣的情形进 行计算,并分析结果,对重要参数的高中低水平进行计算 仿真,考虑放松 条件,假设条件等等。 14 四、美国大学生数学建模竞赛简介: 美国大学生数学建模竞赛简介每年都吸引大量著名高校参 加,近五年,每年有超过 2万个队伍参加,遍及五大洲。我国 学生从1989年(北京大学,清华大学,北京理工大学共四个 队)开始参加每年的一度的 MCM/ICM竞赛。电子科技大学 从1992年开始参加,美国大学生 MCM/ICM 竞赛,获得了比 较好的结果。 MCM/ICM 着重强调研究问题、解决方法的 原创性,团队 合作交流以及结果的合理性。竞赛主要以三个大学生为一组, 在四天时间内,就指定的问题(从 ABCDEF 任选一个),完 成从建立模型、求解验证到论文撰写的全部工作进展。 15 MCM/ICM主要参与国家和地区 • USA, • China, • Canada, • Australia, • Indonesia, • Republic of Korea, • Mexico, • Scotland, • Singapore, • Macau SAR, • South Africa , • United Kingdom . 四、美国大学生数学建模竞赛简介: 16 2020年大学生竞赛获奖情况 (2018年有20602队参加) 奖项 所占比例 Outstanding 0.1% Finalist 1% Meritorious 7% Honorable Mention 40% Successful Participant 51.9% 合计 100% 四、美国大学生数学建模竞赛简介: 17 如何参赛 组队建议 参赛日期:春节前后 月中旬 一人主管建模,一人主管 编程,一人主管写作, 合力完 成整个过程。 由3名大学生生组成参赛队,在指定的 4天内,完成竞赛。 论文要查重。 比赛时间 四、美国大学生数学建模竞赛简介: 转变 学习思维转变 学习态度转变 做题!做题!做题! 着重创新思维、用数学解决实际问题 要我 学习 我要 学习 一. 数学建模简介 《数学建模》课件汇总 第7页,共105页

2021-12-28 《数学建模》课件汇总 一 数学建模组队 合作不当1+1+1+1=0 如队与合作拔巧 各司其积,相互配 强强联合? 合:一人创重建模,一人制 童格加,一人侧童写作,一 取长补短 人精助、协调。 相得益彰 合作共赢1 合作愉快 1+1+1+1=成功 THANKS 第8页,共105页 4
2021-12-28 4 组队与合作技巧 强强联合? 合作共赢! 取长补短 相得益彰 一. 数学建模组队 合作不当 1+1+1+1= 0 各司其职,相互配 合:一人侧重建模,一人侧 重编程,一人侧重 写作,一 人辅助、协调。 合作愉快 1+1+1+1= 成功 21 《数学建模》课件汇总 第8页,共105页

2021-12-28 《数学建模》课件汇总 二.建模案例 第二章数学与现实世界 一从现实世界到数学模型 例2.1渡口模型 数学模型是现实世界与数学世界的理想 一个波口的渡船营运者拥有一只甲板长32米, 桥梁。 可以并排停放两列车柄的渡船。他在考虑怎样 在甲板上安排过河丰柄的位置,才能安全地运 数学模型是对于现实世界的一个特定对 象,为了一个特定目的,根据特有的内在 过最多戴量的车辆。 规律,做出必要的简化假设,运用适当的 数学工具建立的一个数学结构。 分析:怎样安排过河车辆,关心一次可以运 多少辆各类车。 数学遮模国习 数学地习 2 准备工作:观察数日,发现每次情况不尽相 (山应被怎样安排摩托车? 同,得到下列数据和情况: (2)下一辆到达的车是什么类型? ·()车辆随机到达,形成一个等待上船的车列; (③)怎样描述一辆车的车身长度? ●(2)来到车辆中,轿车约占40%,卡车约占55%, (④)如何安排到达车辆加入甲板上两列车队 摩托车的占5%; ●(3)轿车车身长为3.5~5.5米,卡车车身长为 中的哪一列中去? 8≈10米。 问题的解决: 这是一个机理较复杂的随机问题,是遵循 (1)认为摩托车不会占有实际空间。 “先到先服务”的随机排队问题。 (2)确定即将到达车柄类型,利用随机模拟方法。 摩托本 解决方法:采用模拟模型方法。 卡率 桥车 分析:需考意以下问题: 0.55 0.951 数学毫模习 数学地旗习 (③)确定随机到达车柄的身长车。 10次模拟情况,每次1000辆车。 汽车美型及车身长模椒原理分析 (④关于车柄的排放。 车柄数量情况 甲板可停放两列汽车,可供停车的总长为 32×2=64米 排放原则:两列尽可能均衡。(怎样实现?) 结果分析:由一组特定随机数确定车型和车身 长度,仅得到一个解答。 将一短随机敷模拟确定的结果,看成对一火 实际运载情况的“观察”,少数几次观察是无 意义的。 ■系转1目系2■系利由 需多次重复模拟,再进行统计分析 6 第9页,共105页 1
2021-12-28 1 数学建模 1 第二章 数学与现实世界 一. 从现实世界到数学模型 数学模型是现实世界与数学世界的理想 桥梁。 数学模型是对于现实世界的一个特定对 象,为了一个特定目的,根据特有的内在 规律,做出必要的简化假设,运用适当的 数学工具建立的一个数学结构。 数学建模 2 例2.1 渡口模型 一个渡口的渡船营运者拥有一只甲板长 32米, 可以并排停放两列车辆的渡船。他在考虑怎样 在甲板上安排过河车辆的位置,才能安全地运 过最多数量的车辆。 分析:怎样安排过河车辆,关心一次可以运 多少辆各类车。 二. 建模案例 数学建模 3 准备工作: 观察数日,发现每次情况不尽相 同,得到下列数据和情况: l (1)车辆随机到达,形成一个等待上船的车列; l (2)来到车辆中,轿车约占40%,卡车约占55%, 摩托车约占5%; l (3)轿车车身长为3.5~5.5米,卡车车身长为 8~10米。 这是一个机理较复杂的随机问题,是遵循 “先到先服务”的随机排队问题。 解决方法:采用模拟模型方法。 分析:需考虑以下问题: 数学建模 4 (1) 应该怎样安排摩托车? (2) 下一辆到达的车是什么类型? (3) 怎样描述一辆车的车身长度? (4) 如何安排到达车辆加入甲板上两列车队 中的哪一列中去? 问题的解决: (1)认为摩托车不会占有实际空间。 (2)确定即将到达车辆类型,利用随机模拟方法。 0 0.55 0.95 1 卡车 轿车 摩托车 数学建模 5 汽车类型及车身长模拟原理分析 (3) 确定随机到达车辆的身长车。 (4) 关于车辆的排放。 甲板可停放两列汽车,可供停车的总长为 32×2=64米 排放原则:两列尽可能均衡。(怎样实现?) 结果分析:由一组特定随机数确定车型和车身 长度,仅得到一个解答。 将一组随机数模拟确定的结果,看成对一次 实际运载情况的“观察”,少数几次观察是无 意义的。 需多次重复模拟,再进行统计分析 数学建模 6 10次模拟情况,每次1000辆车。 《数学建模》课件汇总 第9页,共105页
2021-12-28 《数学建模》课件汇总 魔桃案例 二,银行贤款问题 查找资料:想行还款方式有些? 等额 你认为:银 加录你想要 还款方式 本金 外选部寧种还 行帝望你遍部 货款投资,林 款方式? 种还款方式? 应诚如何选择? 等额 本息 1 <》 座立 假定你正在考虑月息0.5%、数领为150000元的抵 等颜本全型设a,为第i个月的还款金领。 模型 押货款.如采你每月可以还款2000元,能否在20年还 款后就能还清货款?并啼定你能够借货的最大款项。 4-+c-9r-9+c- 提取变量:题目中廊些变量比较重要? 四个:月悬r、本金C、月还款a、还款期数n a-C+ca-i-br 面城维叶么 公平:借战总价值与还钱总价值相等! + <》 <》 等本全型一一应用】 本息型 动手立预本地型 等额本金还款法计算范例: 如:货款20万元,贷款期为10年,凛如何还款: 每季等额归还本金:200000+(10×4)=5000元 建立模型 RANK 第-个季度利息:200000×(5.58%+4)=2790元 则第一个季度还款额为5000+2790=7790元: 第二个季度利息:(200000-5000×1)×(5.58%÷4)=2720元 r-ca+ry 则第二个季度还款额为5000+2720=7720元 4444 ◆违背了公平原则 第40个度利息:(200000-5000×39)×(5.58%+4)=69.75元 则第40个季度(最后一期)的还款额为5000+69.75=5069.75元 视有 <》s <<》。 第10页,共105页 1
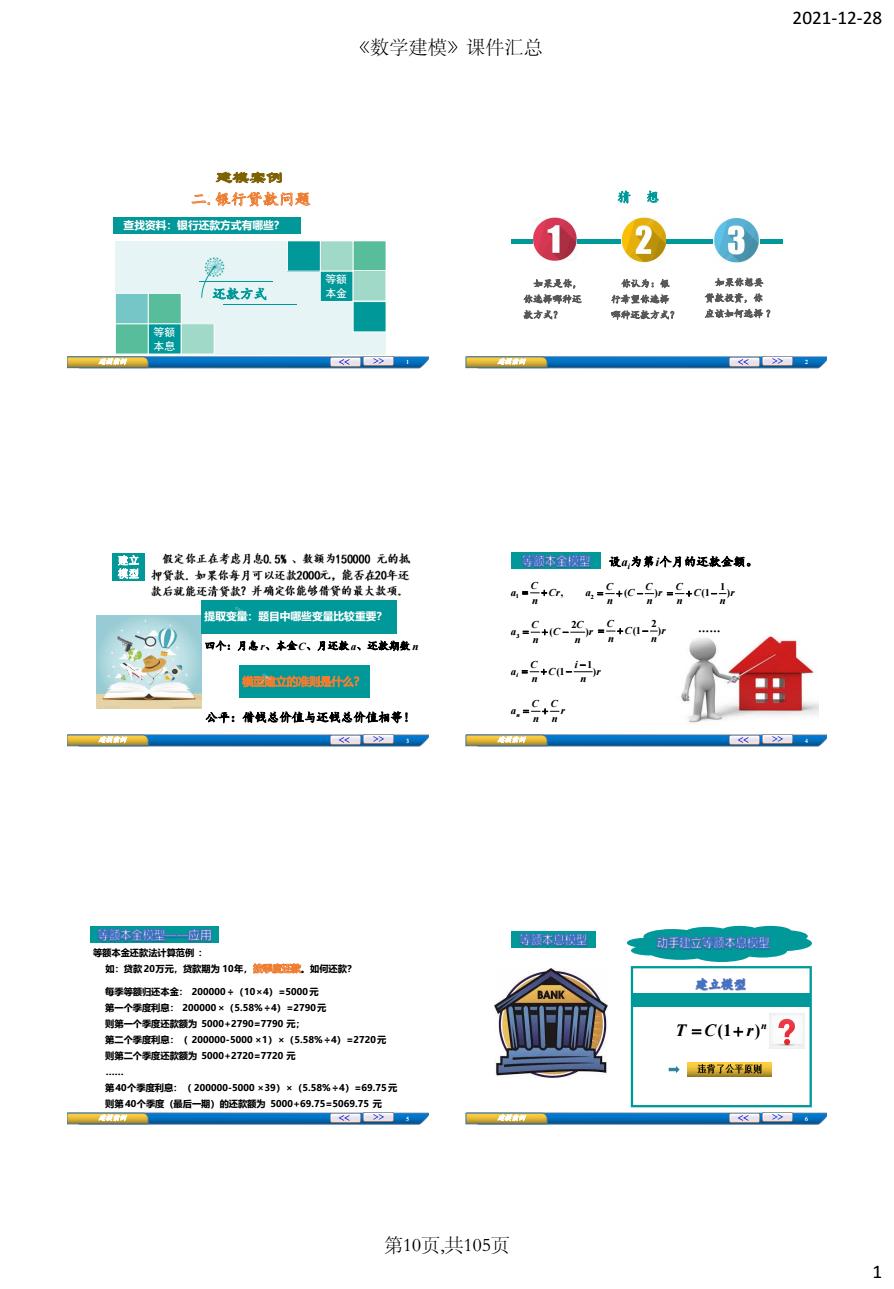
2021-12-28 1 建模案例 1 等额 本金 等额 本息 还款方式 查找资料:银行还款方式有哪些? 建模案例 建模案例 2 如果是你, 你选择哪种还 款方式? 你认为:银 行希望你选择 哪种还款方式? 如果你想要 贷款投资,你 应该如何选择 ? 猜 想 建模案例 3 建立 模型 提取变量:题目中哪些变量比较重要? 四个:月息 r、本金C、月还款a、还款期数 n 公平:借钱总价值与还钱总价值相等! 建模案例 4 , 1 Cr nC a r nC C nC a ( ) 2 r n C nC ) 1 (1 r nC C nC a ) 2 ( 3 r n C nC ) 2 (1 ...... 设ai为第i个月的还款金额。 r n i C nC ai ) 1 (1 r nC nC an 建模案例 5 每季等额归还本金: 200000÷(10×4)=5000元 第一个季度利息: 200000×(5.58%÷4)=2790元 则第一个季度还款额为 5000+2790=7790 元; 第二个季度利息:( 200000-5000 ×1)×(5.58%÷4)=2720元 则第二个季度还款额为 5000+2720=7720 元 ……第40个季度利息:( 200000-5000 ×39)×(5.58%÷4)=69.75元 则第40个季度(最后一期)的还款额为 5000+69.75=5069.75 元 等额本金还款法计算范例 : 如:贷款20万元,贷款期为 10年, 。如何还款? 建模案例 6 n T C(1 r) 《数学建模》课件汇总 第10页,共105页