
第四章 线性判别函数 2010-10-25
第四章 线性判别函数 2010-10-25

引言
引言

3 分类器设计 81 MAX a(x) 样本分布的 决策规则: 训练样本集 统计特征: 判别函数 概率密度函数 决策面方程 判别函数类{g(a),u∈A} 选择最佳准则 决策规则: 训练样本集 判别函数 准则函数L(a) 决策面方程 求a:L(a)=minL(a)
3 分类器设计 MAX g1 . . . g2 gc . . . x1 x2 xn a(x) 训练样本集 决策规则: 判别函数 决策面方程 选择最佳准则 训练样本集 样本分布的 统计特征: 概率密度函数 决策规则: 判别函数 决策面方程

4 线性判别函数的基本概念 口一般形式 权向量 8(X)=wx+0 阈值权 口两类问题的分类规则 g(x)=81(x)-82(x) g(x)>0,则决策X∈0, 如果{g(x)<0,则决策 X∈0) g(x)=0,可将其任意分类或拒绝
4 线性判别函数的基本概念 一般形式 两类问题的分类规则 4 0 ( ) T g x x w 1 2 ( ) 0, ( ) 0, ( ) 0, g g g x x x x x 则决策 如果 则决策 可将其任意分类或拒绝 1 2 gg g () () () xxx 阈值权 权向量

5 线性判别函数的几何意义 y>0 T2 y= :0 y<0 Ri R2 X W (X w X -00 lwlf
5 线性判别函数的几何意义
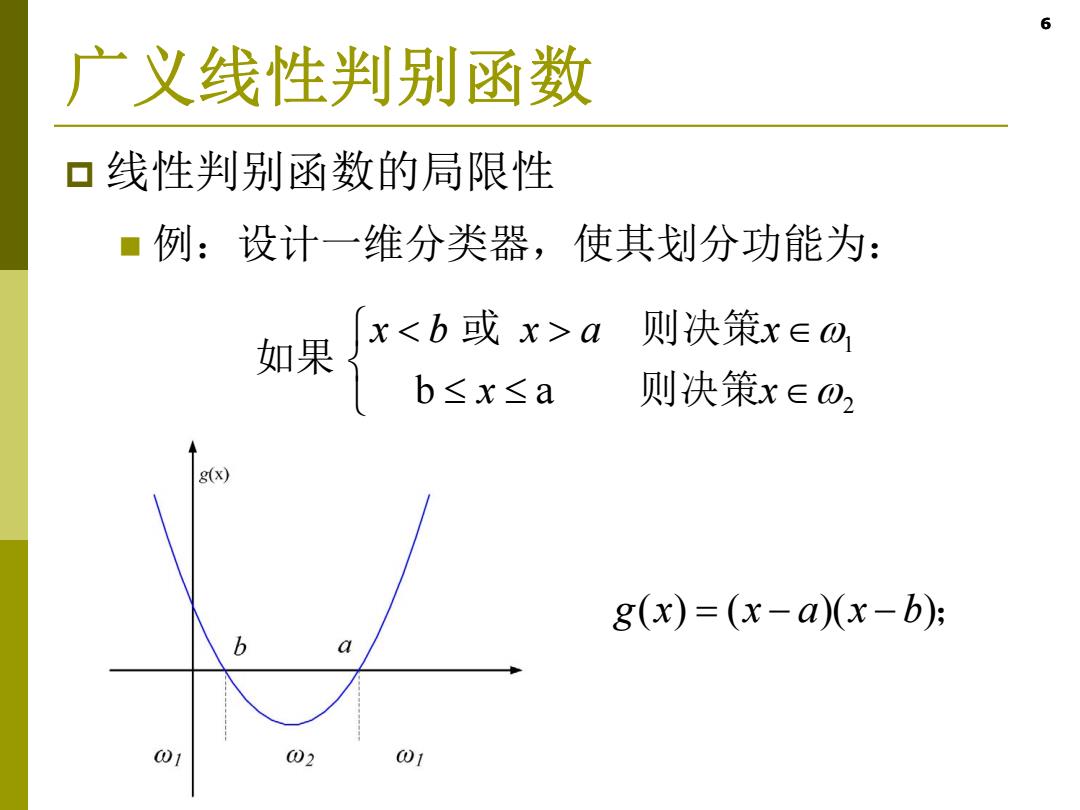
6 广义线性判别函数 口线性判别函数的局限性 ■例:设计一维分类器,使其划分功能为: 如果 xa 则决策x∈o b≤x≤a 则决策x∈ω2 g(x) 8(x)=(x-a)(x-b) 01 02 01
6 广义线性判别函数 线性判别函数的局限性 例:设计一维分类器,使其划分功能为: 6 g( ) ( )( ) x x axb ; 1 2 b a xb xa x x x 或 则决策 如果 则决策

7 广义线性判别函数 口非线性判别函数g(x),通过适当的变换可转化为 线性判别函数g(y) ■例:二次判别函数→广义线性判别函数 8(x)=C+Cx+C2x2; 乃 1 Co y= y2 三 ,8= a 三 C y3 x2 as C2 →g'(y)=ay=∑a,y,=g(x) i=1
7 广义线性判别函数 非线性判别函数 g (x ),通过适当的变换可转化为 线性判别函数 gꞌ( y ) 例:二次判别函数 广义线性判别函数 7 3 1 '( ) ( ). T i i i g a y g x y ay 2 01 2 g( ) x c cx cx ; 1 1 0 2 2 1 2 3 3 2 y 1 a c y x ac y x ac y a , ;
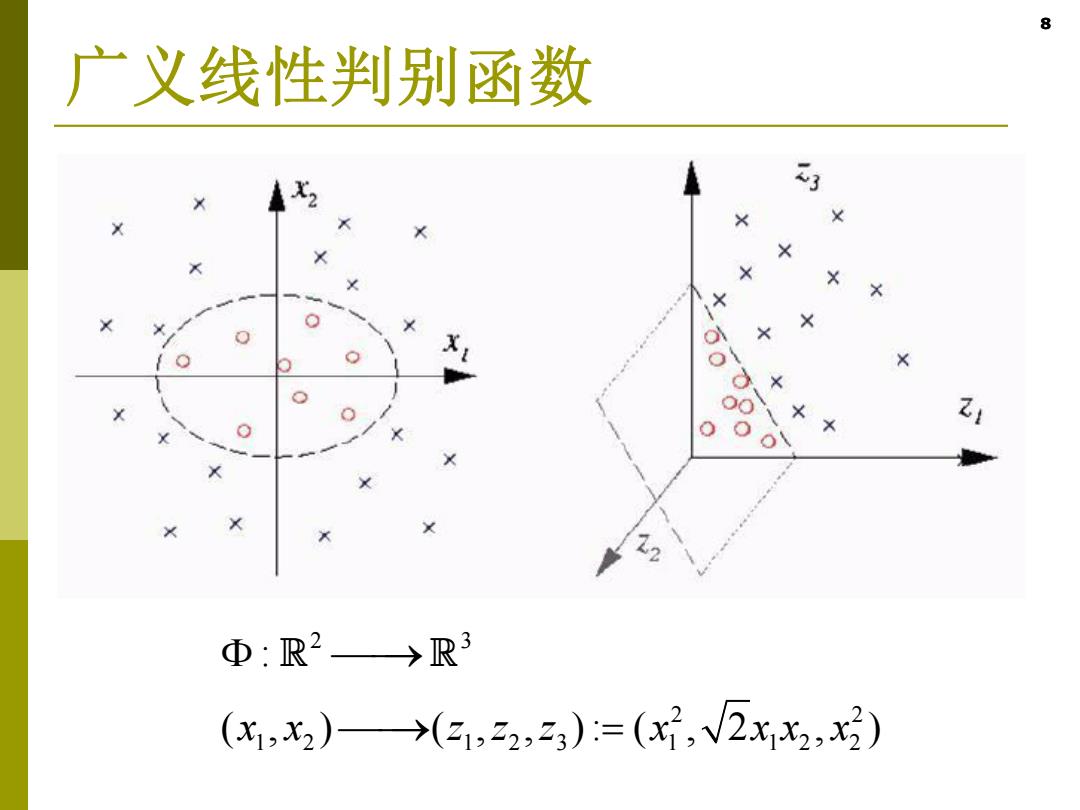
8 广义线性判别函数 X X d 0 Φ:R2→R3 (x,x2)→(31,2,23)=(x2,V2xx2,x)
8 广义线性判别函数 2 3 2 2 1 2 1 2 3 1 12 2 : ( , ) ( , , ): ( , 2 , ) x x z z z x xx x

9 广义线性判别函数 口例:设在三维空间中的分类问题拟采用二次曲面。 如采用广义线性方程求解,试求其广义样本向量 与广义权向量的表达式,及其维数。 axi +bx2+cx;+dx x2 +ex x;++gx+hx2 +l3+m=o a=(a,b,c,d,e,f,g,h,1,m) y=(x2,x2,x32,xx2,x3,x2x3,1,x2,x3,1) z=g(x)=g'(y)=a'y
9 广义线性判别函数 例:设在三维空间中的分类问题拟采用二次曲面。 如采用广义线性方程求解,试求其广义样本向量 与广义权向量的表达式,及其维数。 9

10 广义线性判别函数 口线性判别函数的齐次简化 g(x)=w'x+@o=a'y 1 a Xd wa 1 增广样本向量 增广权向量
10 广义线性判别函数 线性判别函数的齐次简化 10 0 ( ) T T g x wx a y 1 ; 1 1 d x x x y 增广样本向量 1 0 0 ; d w w w a 增广权向量