
数学摸型建立之二 一、 现实量与数学表达式 二、 微分方程建模
一、现实量与数学表达式 二、微分方程建模 数学模型建立之二
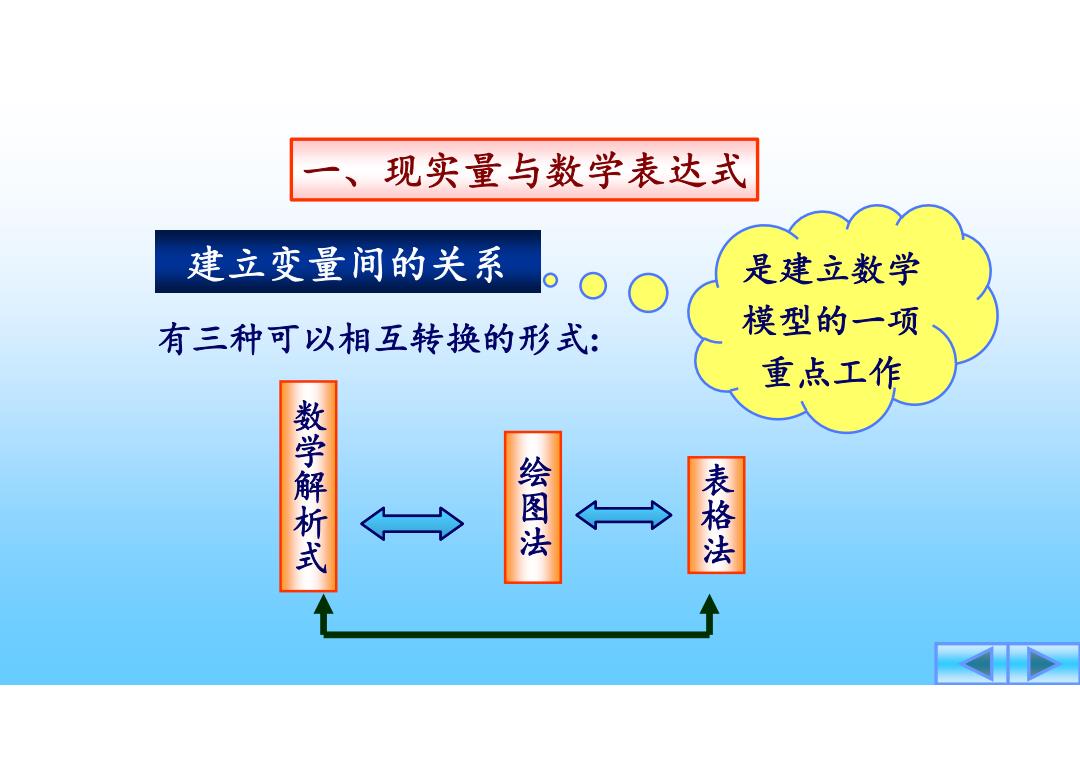
、现实量与数学表达式 建立变量间的关系 是建立数学 有三种可以相互转换的形式: 模型的一项 重点工作 数学解析式 绘图法 表格法
建立变量间的关系 是建立数学 模型的一项 重点工作 一、现实量与数学表达式 绘图法 表格法 数学解析式 有三种可以相互转换的形式 :

例8.1你心中的那场雨 杜甫描述成都的一场春雨 好雨知时节,当春乃发生, 随风潜入夜,润物细无声 若你非遐想花重锦官城的春夜喜雨,享受诵读带来的 愉悦心境,而是感触“春雨贵如油”,关心能否保障农作 物的春种! 问题1你关心的是什么量?降水总量!
例8.1 你心中的那场雨 杜甫描述成都的一场春雨 好雨知时节,当春乃发生, 随风潜入夜,润物细无声. 若你非遐想花重锦官城的春夜喜雨,享受诵读带来的 愉悦心境,而是感触“春雨贵如油”,关心能否保障农作 物的春种! 问题1 你关心的是什么量? 降水总量!
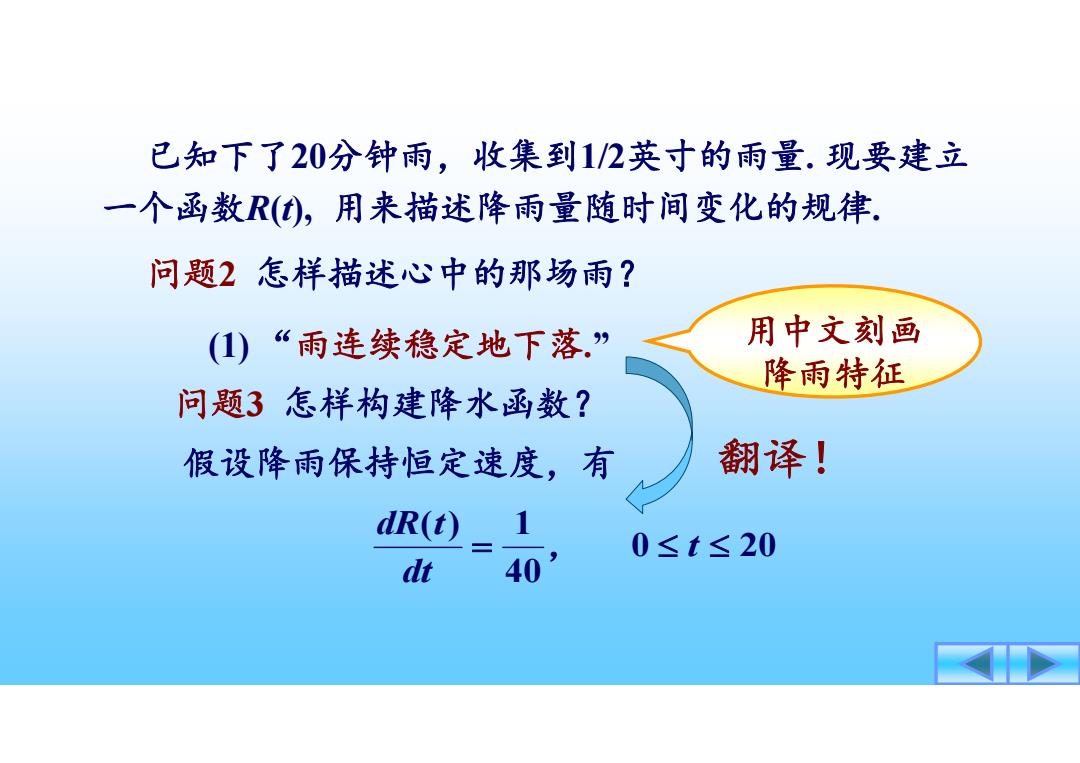
已知下了20分钟雨,收集到1/2英寸的雨量.现要建立 一个函数R(),用来描述降雨量随时间变化的规律. 问题2怎样描述心中的那场雨? ()“雨连续稳定地下落” 用中文刻画 降雨特征 问题3怎样构建降水函数? 假设降雨保持恒定速度,有 翻译! dR(t) 0≤t≤20 dt 40
问题2 怎样描述心中的那场雨? 已知下了20分钟雨,收集到1/2英寸的雨量. 现要建立 一个函数R(t), 用来描述降雨量随时间变化的规律. 问题3 怎样构建降水函数? (1) “雨连续稳定地下落.” 假设降雨保持恒定速度,有 0 20 40 ( ) 1 t dt dR t , 用中文刻画 降雨特征 翻译!

(2)“降雨开始较慢,中间逐渐地加快,达到最大速 度后又减小.” 若假设降雨速度先线性增长后又线性减小,得线性 降雨模型: dR(t) 0.005t, 0≤t≤10; dt 0.1-0.005t, 10<t≤20. 或考虑另一个降雨模型: dR(t)at-bt", a≤t≤b 主观! dt 模型中有两个待定参数a和b. 其它函数?
(2) “降雨开始较慢, 中间逐渐地加快, 达到最大速 度后又减小.” 若假设降雨速度先线性增长后又线性减小, 得线性 降雨模型: 0.1 0.005 , 10 20. ( ) 0.005 , 0 10; t t t t dt dR t 或考虑另一个降雨模型: at bt a t b dt dR t , ( ) 2 模型中有两个待定参数a 和b. 主观! 其它函数?

零件的参数设计一件产品由若千零件组装而成,标 志产品性能的某个参数取决于这些零件的参数,零件参 数包括标定值和容差两部分 1.进行零件参数设计,就是要确定标定值和容差,需 考虑两方面因素; 2.当各零件组装成产品时,如果产品参数偏离预先设 定的目标值就会造成质量损失,偏离越大,损失越大; 3.零件容差的大小决定了其制造成本,容差设计得越 小,成本越高
零件的参数设计 一件产品由若干零件组装而成,标 志产品性能的某个参数取决于这些零件的参数,零件参 数包括标定值和容差两部分. 1.进行零件参数设计,就是要确定标定值和容差,需 考虑两方面因素; 2. 当各零件组装成产品时,如果产品参数偏离预先设 定的目标值就会造成质量损失,偏离越大,损失越大; 3.零件容差的大小决定了其制造成本,容差设计得越 小,成本越高

试通过如下的具体问题给出一般的零件参数设计方法. 粒子分离器某参数(记作y)由7个零件的参数(记作x1, 七2,,x)决定,经验公式为 y=f(1,X2…,X7) 1-2.621-0.36点)2点)6 =142 X X X6X7
试通过如下的具体问题给出一般的零件参数设计方法. 粒子分离器某参数(记作y)由 7个零件的参数 (记作 x 1, x 2 , …, x 7 )决定,经验公式为 6 7 1.16 2 0.56 3/ 2 4 2 4 0.85 2 1 3 2 1 1 2 7 1 2.62 [ 1 0.36 ( ) ] ( ) 174.42 ( )( ) ( , , , ) x x x x x x x x x x x y f x x x

y的目标值(记作yo)为1.50,当y偏离y士0.1时,产品为 次品,质量损失为1000元;当y偏离y0士0.3时,产品为废 品,损失为9000元. 请综合考虑y偏离y,造成的损失和零件成本. 问题5试分析评价以下质量损失函数 成本损 0, y-yo≤0.1 失函数! L(y)=1000 0.1≤y-yo≤0.3 9000 0.3<y-yo
y的目标值(记作y0)为1.50, 当y偏离y0±0.1时,产品为 次品,质量损失为1 000元;当y 偏离y0 ± 0.3时,产品为废 品,损失为9 000元.…… 请综合考虑y偏离y0造成的损失和零件成本. 问题5 试分析评价以下质量损失函数 9000, 0.3 . 1000, 0.1 0.3; 0, 0.1; ( ) 0 0 0 y y y y y y L y 成本损 失函数!

仅为“y的目标值(记为yn)为1.50.当y与y的偏离 为0.1时,产品为次品,质量损失为1000元;当y偏离y0 为0.3时,产品为废品,损失为9000元”的数学语言表达 对损失的理解还应更深入 *此产品只是最终产品的某一部件,y对y,的偏离会 “持续地”影响最终产品的质量; *题目中“如果产品参数偏离预先设定的目标值就会 造成质量损失,偏离越大,损失越大”提示损失是具有 社会性的
仅为“y 的目标值(记为y0)为1.50. 当y与y0的偏离 为0.1时,产品为次品,质量损失为1 000元;当y偏离y0 为0.3时, 产品为废品,损失为9 000元” 的数学语言表达. 对损失的理解还应更深入 * 此产品只是最终产品的某一部件, y 对y0的偏离会 “持续地”影响最终产品的质量; * 题目中“如果产品参数偏离预先设定的目标值就会 造成质量损失,偏离越大,损失越大” 提示损失是具有 社会性的

假设社会质量损失函数Ly)是y一y)的连续函数。 问题6应选择以下哪一个函数? L(y)=k(y-yo) L2(0)=k(y-o) L3(y)=k(Jy-y)月 La(y)=k(y-yo) 常见变量间关系描述: 1.当自变量t变大(小)时,因变量y会怎样变化? 2.有无使y取极大值或极小值的t值? 3.有无使y=0的t值?
假设社会质量损失函数L (y ) 是 (y - y 0 )的连续函数 . 问题6 应选择以下哪一个函数? 2 4 0 L ( y ) k ( y y ) ( ) ( ) 2 0 L y k y y 3 3 0 L ( y ) k ( y y ) ( ) ( ) 1 0 L y k y y 常见变量间关系描述: 1.当自变量 t变大(小)时,因变量 y 会怎样变化? 2. 有无使 y 取极大值或极小值的 t 值? 3. 有无使 y = 0 的 t 值 ?