
第四章 线性判别函数 2010-11-1
第四章 线性判别函数 2010-11-1

最小平方误差准则 (MSE)
最小平方误差准则 (MSE )
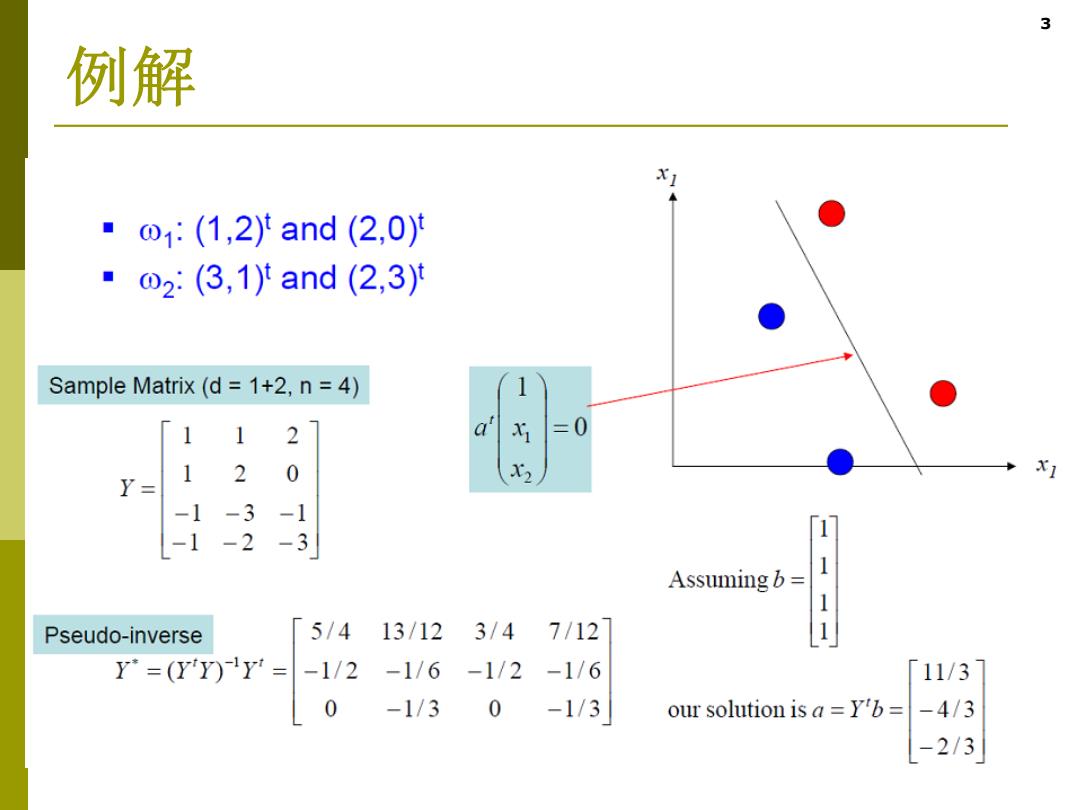
3 例解 ·o1(1,2)and(2,0) ■o2:(3,1)and(2,3) Sample Matrix(d 1+2,n=4) 1 2 1 =0 1 2 0 Y= -3 -1 -2 -3 「1 1 Assuming b Pseudo-inverse 5/4 13/12 3/4 7/12 i Y=(Y)r = -1/2 -1/6 -1/2 -1/6 11/3 0 -1/3 0 -1/3 our solution is a =Y'b= -4/3 -2/3
3 例解

MSE解与Bayes判别函数的关系 当N→∞,b=1n时,MSE的解以最小均方误差 逼近Bayes判别函数:g(x)=p(o|x)-p(o,|x): ■均方误差 e=fa'y-go(x)p(x)dx; 即有a=Y+b=argmine2. J,(a)=∑(a'y,-1)2+∑(ay,+1) X,∈01 X,∈02 =N 〔袋是er+梦m+ X,∈0 X∈02
4 MSE解与 Bayes 判别函数的关系 当 N→∞,b = 1n 时,MSE的解以最小均方误差 逼近 Bayes 判别函数: 均方误差 即有 01 2 gp p () ( xxx | ) ( | ); ;)()( 2 0 2 e dpg xxxyaT * 2 Y e argmin . a b 1 2 1 2 2 2 1 2 2 2 1 2 ( ) ( 1) ( 1) 1 1 ( 1) ( 1) ; i i i i T T si i T T i i J N N N NN NN x x x x a ay ay ay ay

MSE解与Bayes判别函数的关系 J,(a) N =P(@)J(a"y-1)p(xk)dx+P(@.)J(a"y+1)p(xrz)dx =∫(a'y-12pxo)dk+∫(ay-12px,o,)dk -Jtj+l-yoa》-+a p(x) -[(a'y)'p(x)dx-2J(a"y)go(x)p(xx+1 -J[a'y-g(xJp(xdk+[1-Jgi(x)p(xx =e2+[1-g6(x)p(x)本]
5 MSE解与 Bayes 判别函数的关系 2 1 2 1 2 1 2 2 2 1 1 2 2 2 2 1 2 2 0 0 (, ) (, ) (, ) (, ) 2 () (, ) (, ) ( ) ( ) ( 1) ( | ) ( ) ( 1) ( | ) ( 1) ( , ) ( 1) ( , ) () 2 ()() 1 ( ( ) T T T T T T T T T s p p p p pp p d p P p dP p d pd pd pd g pd g J N x x ay x x ay x x x x x ay x x ay x x ay x x ay x x ay x x ay x x x a y a 2 0 2 0 2 2 ) () 1 ()() 1 ()() ; pd g p e gp d d x xx x xx x xx

6 求解MSE解 口计算a*=Yrb,其中YT=(YTY)1YT; 口梯度下降法 VJ.(a)=>2(ay,-b)y,=2Y(Ya-b) a(1),任意初始化 a(k+1)=a(k)-n(k)Y(Ya-b) until VJ,(a≤0或者la(k+1)-a(k)‖≤ 可选7(k)=7(1)/k(7(1)>0)
6 求解MSE解 计算 a*=Y†b,其中 Y† = (YTY)-1YT; 梯度下降法 1 ( ) 2( ) 2 ( ) N T T s i ii i J bY Y a a y y a b (1), ( 1) ( ) ( ) ( ) until ( ) ( 1) ( ) ; ( ) (1) ( (1) 0). T s k k kY Y J kk k k a a a ab a aa 任意初始化 或者 可选

7 求解MSE解 口单样本修正法(Widrow-Hoff算法,LMS) a(1),任意初始化 a(k+1)=a(k)+n(k)(b -a(k)y*)y 其中y是使得a(k)Iy≠b的样本。 Algorithm 10 (LMS) 1 begin initialize a,b,criterion 0,n(),k=0 2 dok←-k+1 3 a←a+(k)(bk-ayk)yk 4 until n(k)(bk -a'yk)y<0 5 return a 6 end
7 求解MSE解 单样本修正法(Widrow-Hoff 算法,LMS) (1), ( 1) ( ) ( )( ( ) ) ( ) Tk k k k Tk k k k kb k k b a a a a yy y ay 任意初始化 其中 是使得 的样本

8 讨论 4 2 2 X X X 0 0 X 8 -2 88g 4 -6 -6 第 -8 -8 4 -2 0 2 4 6 8 -4 -2 0 2 4 6 8
8 讨论

最小错分样本准则
最小错分样本准则

10 简介 口基本思想:对于规范化的增广样本向量,寻找增 广权向量使得不等式组ay>0,i=1,,N中尽 可能多的不等式成立;可引入余量b增加解的 可靠性。 口准则函数:只考虑被错分样本,即只有被错分的 样本aTy<b有贡献,即 J(a)=(Ya-b)-Ya-b; ■求解:无约束最优化的各种算法, 如共轭梯度 法;带约束的二次规划
10 简介 基本思想:对于规范化的增广样本向量,寻找增 广权向量使得不等式组 aTyi ﹥0, i = 1, …, N 中尽 可能多的不等式成立;可引入余量 b 增加解的 可靠性。 准则函数:只考虑被错分样本,即只有被错分的 样本 aTyi ﹤bi 有贡献,即 求解:无约束最优化的各种算法,如共轭梯度 法;带约束的二次规划。 JY Y () ( ) ; a ab ab