北京大学：《模式识别》课程教学资源（课件讲稿）贝叶斯决策理论（第二部分）

2010/9/27 基于最小风险的贝叶斯决策 口定义 第二章贝叶斯决策理论 ■状态空间2：由c个可能的状态(c类)组成 2={0,02,…,0} 2010.09.27 ■决策空间：由所有可能采取的决策组成 月={a,a2,…,ag} ■损失函数(a,0,i=1,…,k,j=1,…,c: 表示对真实状态为@，的样本，采取决策α，时所 造成的损失。 基于最小风险的贝叶斯决策 基于最小风险的贝叶斯决策 口条件期望损失（条件风险）：对于特定的观察 样本x(特征向量)，决策a,造成的损失对x 实际所属类别的各种可能的平均： 6》 4》 R(a,Ix)=E[(a,0,) =22(a,o,P(o,lx) 口期望风险：对所有x取值所作的决策α(x)所带来 的平均风险，即条件风险对x的数学期望。 决策表 R(a)=E[R(a(x)lx】=∫R(a(x)lx)p(x)ds 基于最小风险的贝叶斯决策 基于最小风险的贝叶斯决策 口目标：最小化决策所带来损失的平均值一（平均） 口两类别问题 风险 ·行为a:deciding, 口决策规则 ·行为a2:deciding: Decide a.if R(ax)=min R(a,x) ·损失=(a,0,),1,=1,2. 口最小风险决策的计算步骤 ■条件风险 ·计算后验概率)计算每个决策的条件风险 依据最小条件风险决策 R(a1Ix)=P(o1|x)+元2P(02|x) R(a2 Ix)=42P(@Ix)+422P(02 Ix) 1

2010/9/27 1 第二章 贝叶斯决策理论 2010.09.27 2 基于最小风险的贝叶斯决策  定义  状态空间Ω：由c个可能的状态（ c类）组成  决策空间A：由所有可能采取的决策组成  损失函数 ： 表示对真实状态为ωj 的样本，采取决策 时所 造成的损失。 i i k j c i j ( , ), 1,, , 1,, { , , , }   1 2  c { , , , } Α  1  2   k 3 基于最小风险的贝叶斯决策 决策表 4 基于最小风险的贝叶斯决策  条件期望损失（条件风险）：对于特定的观察 样本 x（特征向量），决策 造成的损失对 x 实际所属类别的各种可能的平均：  期望风险：对所有 x 取值所作的决策α(x)所带来 的平均风险，即条件风险对 x 的数学期望。 i 1 ( |) ( , ) ( , )( |) i ij c ij j j R E P               x x R ( ) [ ( ( ) | )] ( ( ) | ) ( )     ER R p d  xx xx xx 5 基于最小风险的贝叶斯决策  目标：最小化决策所带来损失的平均值—（平均） 风险  决策规则  最小风险决策的计算步骤  计算后验概率  计算每个决策的条件风险  依据最小条件风险决策 1, , , if ( | ) min ( | ) kk i j a Decide R R    x x   6 基于最小风险的贝叶斯决策  两类别问题  条件风险 1 1 2 2 ij j : deciding ; : deciding ; ( , ), , 1, 2. i i j            行为 行为 损失 1 11 1 12 2 2 21 1 22 2 ( |) ( |) ( |) ( |) ( |) ( |) R PP R PP           xxx xxx

2010/9/27 基于最小风险的贝叶斯决策 基于最小风险的贝叶斯决策 口两类别问题 口例：两类细胞识别问题：正常类和异常类 ■决策规则 ■根据已有知识和经验，两类的先验概率： 正常(o):P(o)=0.9 Decide fo,if ()P(Ix)>()P(@1x) 0,otherwise 异常(o,)：P(o)=0.1 对某一样本观察值x,通过计算或查表得到： if P(x)(2)P(@) p(xlo,)-0.2,p(xlo.)=0.4 Decide P(xo2)(-2i)P(a) ,otherwise 入1=0，入12=6，入21=1，入2=0 ■依据最小风险决策如何对细胞x进行分类？ 基于最小风险的贝叶斯决策 两种决策方法之间的关系 口解： 2a,0,)= 0,i=j 0.9×0.2 山，i≠ ，i,j=1,…,c P(a x)= 0.9x02+0.1x0.4=0.818 P(@1x) 0.4×0.1 02x0.9+0.4×0=0.182 R(a,Ix)=2(a.0,)P(@,Ix) J- Ra1国-2，PO,l)=2Pal)=1.092, P(o,1x)=1-P(o,Ix) R41国=2PO,1x)=2,Pax)=0818 min R(a,Ix)max P(o,Ix) .R(ax)>R(a x),.Decide a,xe 2 两种决策方法之间的关系 Neyman-Pearson决策 A12>入21 口两类错误率 ■令R是整个特征空间，R,是类别o1的决策域， R是类别o2的决策域：R+R2-R。 P(error)=SP(o.s+P(.)d =Jpa)P(a达+∫pxa)Pah =P(@:)Jp(xIo.)dx+P(@p(xl@)dx 。=P(e:)P(o) cision regions 0,P(oNini P(o,P.(error)P(@P(error) P()-in) 两类错误率 2

2010/9/27 2 7 基于最小风险的贝叶斯决策  两类别问题  决策规则 1 21 11 1 12 22 2 2 , if ( ) ( | ) ( ) ( | ) Decide , otherwise      P P       x x 12 22 2 1 2 21 11 1 2 1 ( )() , if > Decide ( )() , otherwise (| ) ( | ) P P P P                x x 8 基于最小风险的贝叶斯决策  例：两类细胞识别问题：正常类和异常类  根据已有知识和经验，两类的先验概率： 正常（ω1）： P(ω1) = 0.9 异常（ω2）： P(ω2) = 0.1 对某一样本观察值 x，通过计算或查表得到： p(x|ω1)=0.2， p(x|ω2)=0.4 λ11=0， λ12=6， λ21=1， λ22=0  依据最小风险决策如何对细胞 x 进行分类？ 9 基于最小风险的贝叶斯决策  解： 1 2 2 1 1 12 2 1 2 2 2 21 1 1 1 2 22 0.9 0.2 ( | ) 0.818, 0.9 0.2 0.1 0.4 0.4 0.1 ( | ) 0.182; 0.2 0.9 0.4 0.1 ( | ) ( | ) ( | ) 1.092, ( | ) ( | ) ( | ) 0.818; ( | ) ( | ), Decide , . j j j j j j P P R PP R PP R R                              x x x xx x xx  xx x 10 两种决策方法之间的关系 0, ( , ) , , 1, , . 1, i j i j ij c i j           1 1, ( |) ( , )( |) ( |) 1 ( |) c i ij j j c j i j ji R P P P               x x x x min ( | ) max ( | ) R P i i    x x   11 两种决策方法之间的关系 当前无法显示此图像。 (decision regions) 2 1 ( )/ ( )  a  P P   2 12 22 1 21 11 ( )( ) ( )( ) b P P           12 Neyman-Pearson 决策  两类错误率  令 R 是整个特征空间，R1 是类别ω1的决策域， R2 是类别ω2的决策域：R1 + R2= R。 1 2 1 2 1 2 2 1 2 2 11 2 21 1 2 2 11 ( ) ( ,) ( ,) (| )( ) (| )( ) ( ) (| ) ( ) (| ) ( )( ) ( )( ) R R R R R R P error P d P d p Pd p Pd P p dx P p d P P error P P error                        xx xx x xx x x xx 两类错误率

2010/9/27 14 Neyman-Pearson决策 Neyman-Pearson决策 口决策目标：在Pz(emor)=eo条件下，求P(emo) 口决策目标：极小化Y 极小值。 ■根据Lagrange乘子法 y=(1-16)+J [ap(x)-p(xx: 或者 y=P(error)+(P(error)-5o), y=(1-)+J [p(xlo,)-ip(x: 其中，是Lagrange乘子，目标是求y的极小值。 fp(xlo)ds=6o. 注意：R(ero)=pxah=l-po 头=0st=pIo2 B(error)=Jp(xl0.)ds=1-Jp(xl0.)ds=o p(to) 16 Neyman-Pearson决策 Neyman-Pearson决策 口决策准则 口例：一个两类问题中，模式均为二维正态分布， g if ip)p().then xe 其均值矢量和协方差阵分别为： lo. 4=(-1,0),4=(1,0,8,=82=1 or =pa2> 设，=0.09，求Neyman-Pearson的决策阈值。 i,then x∈t a po2)< 02 ■解： =立[-aa-小云[6++ →N-P决策规则归结为寻找阀值入，使得 s云n-%-小立6-+ p(xlo yds=6o .p(xl)=exp(-2x,) p(xl) Neyman-Pearson决策 Neyman-Pearson决策 口解：判决准则 口解：通过计算P(error)=o求解入： 任e22te5ame侵 B(error)=p(xo)ds .对于不同的元，决策边界是平行于x,的不同直线。（如图） -+正k 2 4 2 1 1/2 1/4 00.0460.0890.0159 0.2580.378 4 与的关系表 3

2010/9/27 3 13 Neyman-Pearson 决策  决策目标：在 P2(error)=ε0条件下，求 P1(error) 极小值。  根据Lagrange乘子法 其中λ是Lagrange乘子，目标是求γ的极小值。 1 20    P error P error ( ) ( ( ) ),   2 1 1 2 1 11 2 2 20 ( ) (| ) 1 (| ) ; ( ) (| ) 1 (| ) . R R R R P error p d p d P error p d p d               xx xx xx xx 注意： 14 Neyman-Pearson 决策  决策目标：极小化γ 1 2 0 21 0 12 (1 ) [ ( ) ( )] (1 ) [ ( ) ( )] R R p pd p pd                   x xx x xx ； 或者 ； . ( | ) ( | ) 0 0 ( | ) , 2 * 1 * * 2 0 1         t t t x x p p p d R            15 Neyman-Pearson 决策  决策准则 N-P决策规则归结为寻找阈值λ，使得 1 2 1 2 1 1 2 2 if ( ) ( ), then or ( ) ( ) , then ( ) p p p l p                     xx x x x x x 1 2 0 (| ) . R p d     x x 16 Neyman-Pearson 决策  例：一个两类问题中，模式均为二维正态分布， 其均值矢量和协方差阵分别为：  解： 1 2 12 ( 1,0) , (1,0) , . T T         I 0 设 ， 0.09 Neyman-Pearson   求 的决策阈值。               2 2 1 11 12 2 2 2 22 12 1 1 2 11 11 ( | ) exp exp 1 ; 22 22 11 11 ( | ) exp exp 1 ; 22 22 (| ) exp( 2 ). (| ) T T p xx p xx p x p                                              x xx x xx x x 17 Neyman-Pearson 决策  解：判决准则 1 1 2 2 1 if exp( 2 ) i e , th 1 - ln 2 en ; x x x               ， . . x 对于不同的 ，决策边界是平行于 的不同直线。（如图） 18 Neyman-Pearson 决策  解：通过计算 P2(error)=ε0求解λ： 1 2 2 1 2 2 ln 2 1 2 2 1 1 2 ln 2 1 1 ( ) (| ) 1 ( 1) exp 2 2 1 ( 1) exp . 2 2 R P error p d x x dx dx x dx                                  x x  4 2 1 1/2 1/4 0 0.046 0.089 0.0159 0.258 0.378  0 与 的关系表 

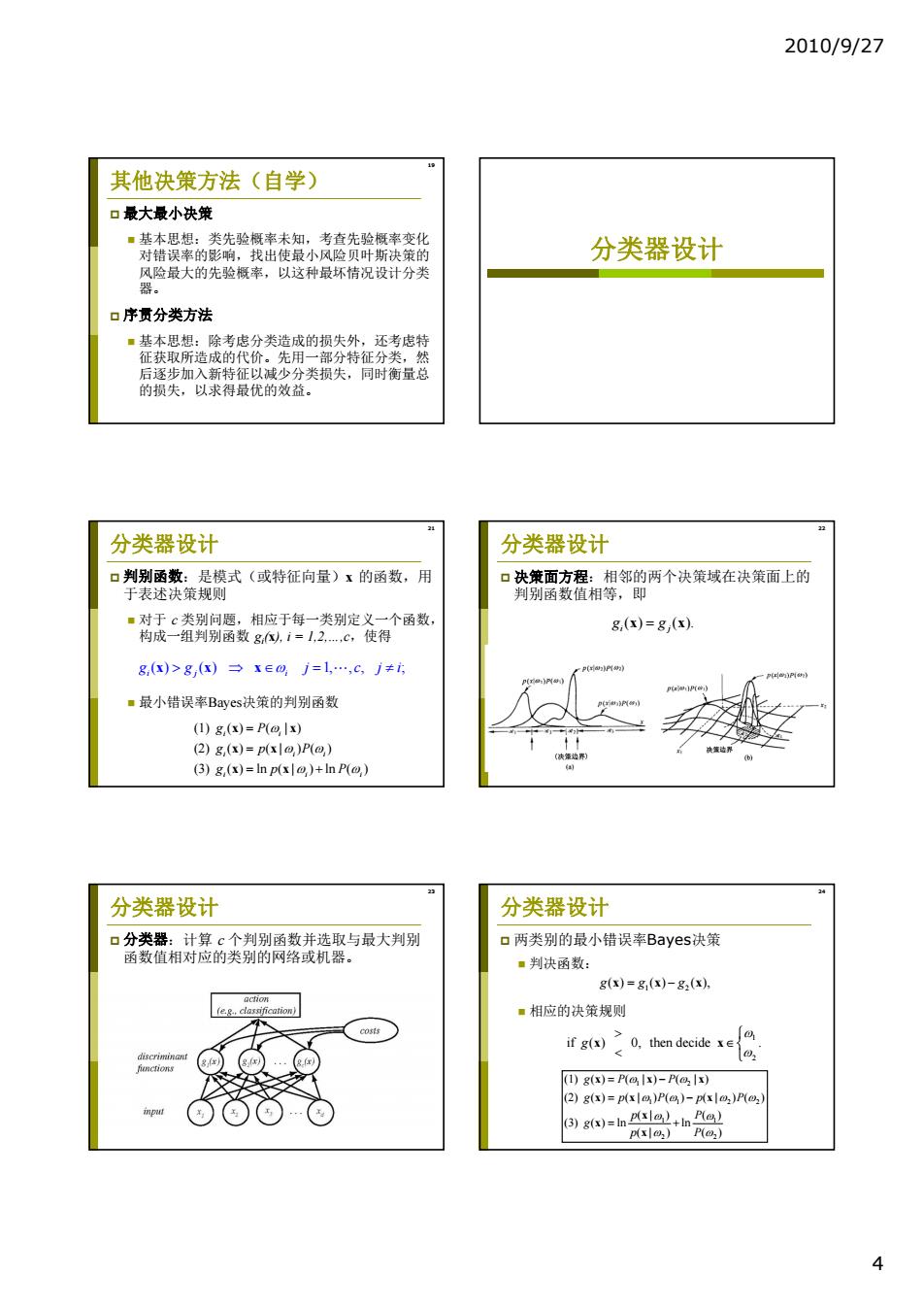
2010/9/27 其他决策方法（自学） 口最大最小决策 ■基本思想：类先验概率未知，考查先验概率变化 对错误率的影响，找出使最小风险贝叶斯决策的 分类器设计 风险最大的先验概率，以这种最坏情况设计分类 器。 口序贯分类方法 ·基本思想：除考虑分类造成的损失外，还考虑特 征获取所造成的代价。先用一部分特征分类，然 后逐步加入新特征以减少分类损失，同时衡量总 的损失，以求得最优的效益。 22 分类器设计 分类器设计 口判别函数：是模式（或特征向量）x的函数，用 口决策面方程：相邻的两个决策域在决策面上的 于表述决策规则 判别函数值相等，即 ■对于c类别问题，相应于每一类别定义一个函数， 8,()=8(x) 构成一组判别函数g,i=1,2…,c,使得 g()>8()→x∈0，j=1,…,c,j≠i p()P() ■最小错误率Bayes决策的判别函数 (1)g,(x)=P(@,Ix) (2)g,(x)=p(xlo,)P(@,) (3)g(x)=lnp(x|@)+lnP(@) 分类器设计 分类器设计 口分类器：计算c个判别函数并选取与最大判别 口两类别的最小错误率Bayes决策 函数值相对应的类别的网络或机器。 ■判决函数： g(x)=8(x)-g2(x), action ■相应的决策规则 if g(x)> O,then decide x∈ discriminant funcnons (1)8(x)=P(@lx)-P(@Ix) (2)g(x)=p(xIo)P()-p(xlo:)P(o: 3)8(x)=Inn P(o) p(xlo)P(o) 4

2010/9/27 4 19 其他决策方法（自学）  最大最小决策  基本思想：类先验概率未知，考查先验概率变化 对错误率的影响，找出使最小风险贝叶斯决策的 风险最大的先验概率，以这种最坏情况设计分类 器。  序贯分类方法  基本思想：除考虑分类造成的损失外，还考虑特 征获取所造成的代价。先用一部分特征分类，然 后逐步加入新特征以减少分类损失，同时衡量总 的损失，以求得最优的效益。 分类器设计 21 分类器设计  判别函数：是模式（或特征向量）x 的函数，用 于表述决策规则  对于 c 类别问题，相应于每一类别定义一个函数， 构成一组判别函数 gi (x), i = 1,2,…,c，使得  最小错误率Bayes决策的判别函数 ( ) ( ) 1, , , ; ij i g xx x     g j cji   (1) ( ) ( | ) (2) ( ) ( | ) ( ) (3) ( ) ln ( | ) ln ( ) i i i ii i ii g P gpP gp P          x x x x x x 22 分类器设计  决策面方程：相邻的两个决策域在决策面上的 判别函数值相等，即 ( ) ( ). i j g g x x  23 分类器设计  分类器：计算 c 个判别函数并选取与最大判别 函数值相对应的类别的网络或机器。 24 分类器设计  两类别的最小错误率Bayes决策  判决函数：  相应的决策规则 1 2 gg g ( ) ( ) ( ), xxx   1 2 11 2 2 1 1 2 2 (1) ( ) ( | ) ( | ) (2) ( ) ( | ) ( ) ( | ) ( ) (| ) ( ) (3) ( ) ln ln (| ) ( ) gP P gp P p P p P g p P                xxx xx x x x x 1 2 if ( ) 0, then decide . g        x x

2010/9/27 分类器设计 口两类别的最小错误率Bayes决策 正态分布的 ·决策面方程 最小错误率贝叶斯决策 g()=0. ·分类器 值单元 决 单变量的正态分布 单变量的正态分布 A bell-shaped distribution defined by the probability density function 口p(x)完全由u与o2确定，常记作N(4,G2) 1 口正态分布的熵(entropy)在所有的已知均值及方 p(x)= 2aoe。 1 差的分布中最大。 It the random variable x follova a normal diatribution,then 口px)关于均值对称，最大值位于x=μ处， ThPea414 ty that Y w411ga114 nto the aterva1{w,b】w 1 p)= .Expected,or mean,value of X is EX灯=Jp(xd冰=u √2πG Var(x)=ET(x-u)]=(x-u)p(x)dx a' Standard deviation of x,a',is 0,=0 多元正态分布 多元正态分布 口概率密度函数 口均值μ和协方差矩阵 1 p(x)= 2 exp←-rza-》 μ=E=∫xp(x)dk 2=Ex--μ]=∫(x-)x-四'px)k 其中： =Ex,]=xp(x,)dx, 1=[:,x,,x是d维列向量(T表示向量的转置)： o=E(3-4x,-4门=∬(x-4,-4,'pxx,本 μ=[4,4，…，4了是d维均值向量： Σ是d×d协方差矩阵： Σ= E(x-4)门 是Σ的逆矩阵，四是Σ的行列式。 E(x2-4x-4】 5

2010/9/27 5 25 分类器设计  两类别的最小错误率Bayes决策  决策面方程  分类器 g( ) 0. x  正态分布的 最小错误率贝叶斯决策 27 单变量的正态分布 28 单变量的正态分布  p(x) 完全由μ与σ2确定，常记作N(μ, σ2)。  正态分布的熵(entropy)在所有的已知均值及方 差的分布中最大。  p(x) 关于均值对称，最大值位于 x=μ处， . 2 1 ( )  p   29 多元正态分布  概率密度函数 1 1 1/2 2 / 2 1 2 1 2 1 1 ( ) exp( ( ) ( )), (2 ) [ , , , ] [ , , , ] T d T d T d p xx x d T d d d            x x μ Σ x μ Σ x μ Σ Σ Σ ΣΣ   其中： 是 维列向量( 表示向量的转置)； 是 维均值向量； 是 协方差矩阵； 是 的逆矩阵， 是 的行列式。 30 多元正态分布  均值μ和协方差矩阵Σ [] () ; [( ) ] ( ( ) ; T T E pd E p d       μ x xxx Σ x -μ)(x -μ x -μ)(x -μ) xx [( )( ) ] ( )( ) ( , ) . [ ] ( ) 2 i j i j T i i j j T ij i i j j i i i i i E x x x x p x x dx dx E x x p x dx                 . [( )( )] [( ) ] [( ) ] [( )( )] 2 2 2 21 2 12 2 1 2 2 2 1 1 2 2 1 1 2 2 2 1 1                          E x u x u E x u E x u E x u x u