
§5.2可分空间 定义5.2.1 设X是一个拓扑 空间,DGX:如果D=乃 则称D是X的一个稠密子集
§5.2 可分空间 定义5.2.1 设X是一个拓扑 空间, .如果 , 则称D是X的一个稠密子集. D X D X =

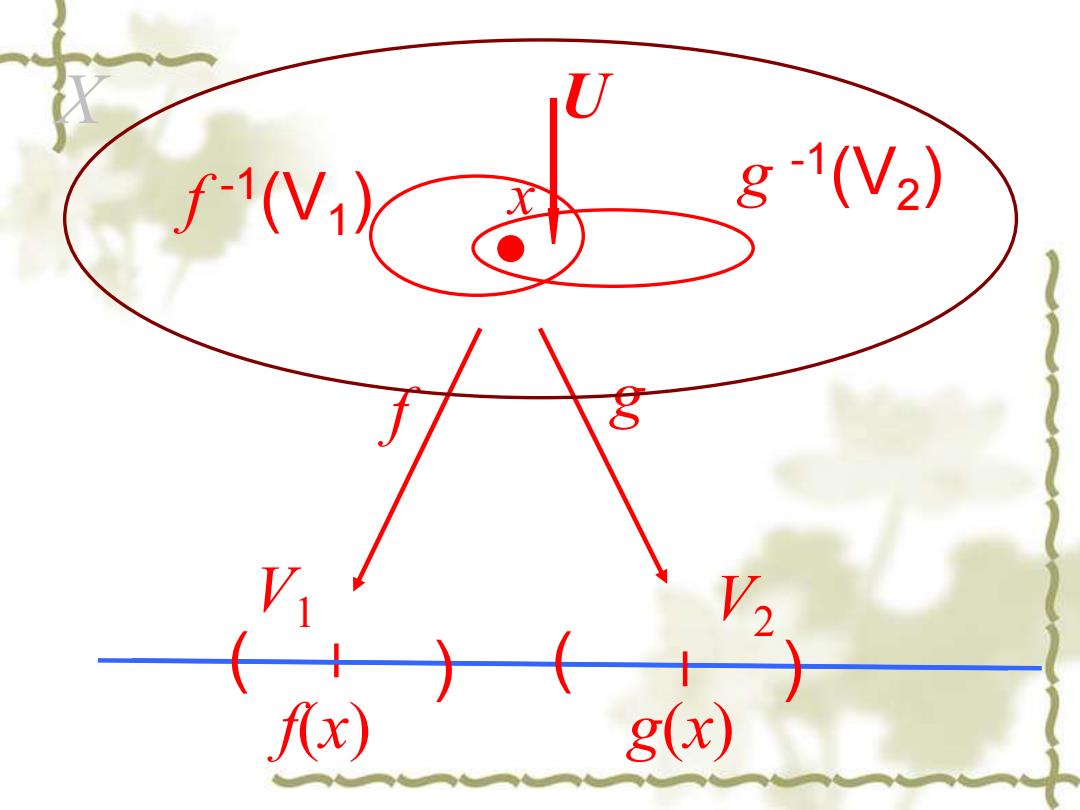
定理5.2.1 设X是一个拓 扑空间,D是X中的一个稠密 子集.又设f,g:X→R青 都是连 续映射,如果flD=glD, 则f=g
定理5.2.1 设X是一个拓 扑空间,D是X中的一个稠密 子集.又设 都是连 续映射,如果 , 则f = g. f g X R , : → | | D D f g =
U f1(V1 g1N2) A fx) 8(x)
f(x) g(x) x ( ) ( ) V1 V2 f g f -1 (V1 ) g -1 (V2 ) X U

定义5.2.2 设X是一个拓 扑空间.如果X中有一个可数 稠密子集,则称X是一个可分 空间
定义5.2.2 设X是一个拓 扑空间.如果X中有一个可数 稠密子集,则称X是一个可分 空间.

定理5.2.2每一个满足第二 可数性公理的空间都是可分空间 继续
定理5.2.2 每一个满足第二 可数性公理的空间都是可分空间. 继续

证朗设X是-个满足第可数性公理的空间,3是它的· 个可数基在中的年-个控元素B中任意取定-个点 B.令 D=iBC黑,8≠

这是个可数集由于X中的每一个排空开集都能够表示为勇中 若干个元素其中当然至少会有-个不是空集之并,因此这个非 空开集-定与D有韩空的交,所以可数集D是X的个稠密 集

推论5.2.3满足第二可 数性公理的空间的每一个子 空间都是可分的
推论5.2.3 满足第二可 数性公理的空间的每一个子 空间都是可分的

定理5.3.2逆不成立 可分性出不具有可遗传性 (见例5.2.1) 继续
定理5.3.2逆不成立 可分性出不具有可遗传性 (见例5.2.1) 继续

例52,1设(X,S是-个拓扑空间,0是任何-个不属于 X的元素(例如我们可以取∞=X).令X'=XUoo和=A U∞AU0,容易验证(请读者記证明)(X,S)是 一个拓扑空间