
随机地程及应用 精品课程 第0章序言
第0章 序言

序言 一、研究对象 随机过程 在许多实际问题中,不仅需要对随机现象做 特定时间点上的一次观察,且需要做连续不断 的观察,以观察研究对象随时间推移的演变过 程
序 言 一、研究对象 在许多实际问题中,不仅需要对随机现象做 特定时间点上的一次观察,且需要做连续不断 的观察,以观察研究对象随时间推移的演变过 程. 随机过程

古埃及人把尼罗河涨落的情况逐天记录下来, 就构成所谓的时间序列。对这个时间序列长 期的观察使他们发现尼罗河的涨落非常有规 律。由于掌握了尼罗河泛滥的规律,使得古 埃及的农业迅速发展,从而创建了埃及灿烂 的史前文明。 尼罗河泛滥期 1月1日 6月17日 10月 12月 “落泪夜
古埃及人把尼罗河涨落的情况逐天记录下来, 就构成所谓的时间序列。对这个时间序列长 期的观察使他们发现尼罗河的涨落非常有规 律。由于掌握了尼罗河泛滥的规律,使得古 埃及的农业迅速发展,从而创建了埃及灿烂 的史前文明。 1月1日 6月17日 10月 12月 尼罗河泛滥期 “落泪夜
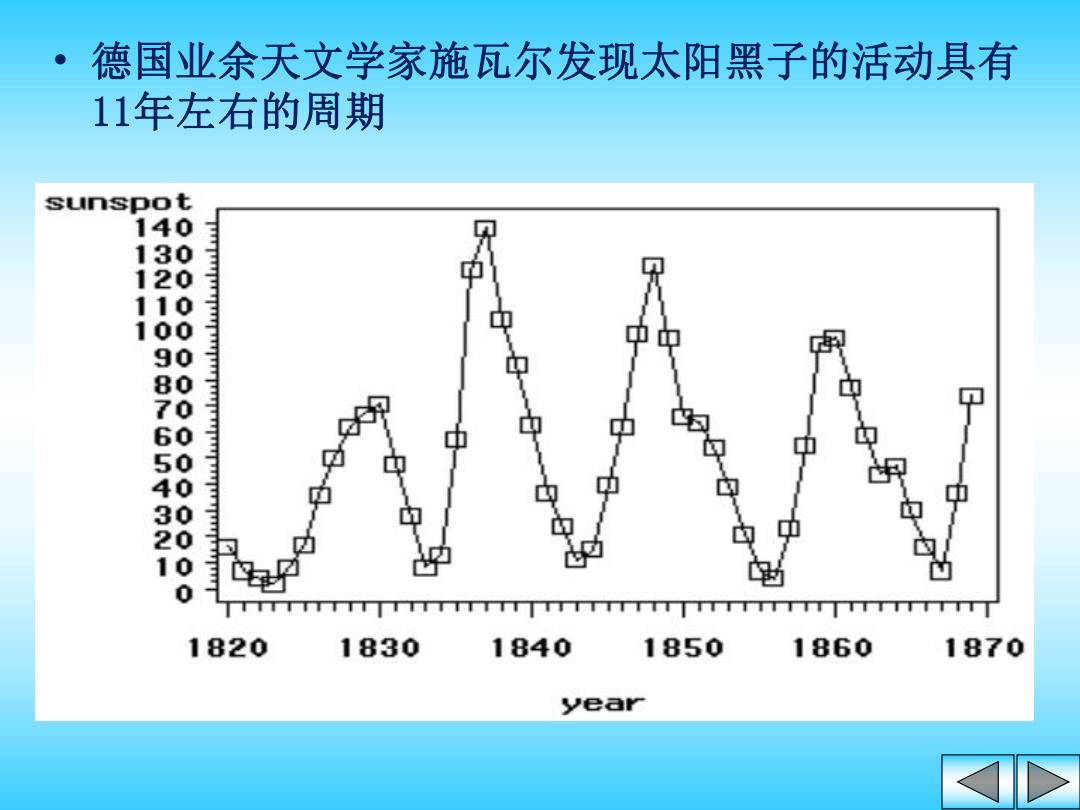
德国业余天文学家施瓦尔发现太阳黑子的活动具有 11年左右的周期 sunspot 140 130 中 1820 1830 1840 1850 1860 1870 year
• 德国业余天文学家施瓦尔发现太阳黑子的活动具有 11年左右的周期

冰川运动
冰川运动

冰川消融
冰川消融

据四川台网测定:截止2008年7月8日8时, 汶川8.0级地震余震区共发生16299次余震, 其中4.0~4.9级198次,5.0~5.9级28次, 6.0~6.9级5次,最大震级为6.4级。 汶川余震序列 汶川余震地,点图 汶川余震序列图1 汶川余震序列图2
汶川余震序列 汶川余震序列图1 汶川余震地点图 据四川台网测定:截止2008年7月8日8时, 汶川8.0级地震余震区共发生16 299次余震, 其中4.0~4.9级198次,5.0~5.9级28次, 6.0~6.9级5次,最大震级为6.4级。 汶川余震序列图2
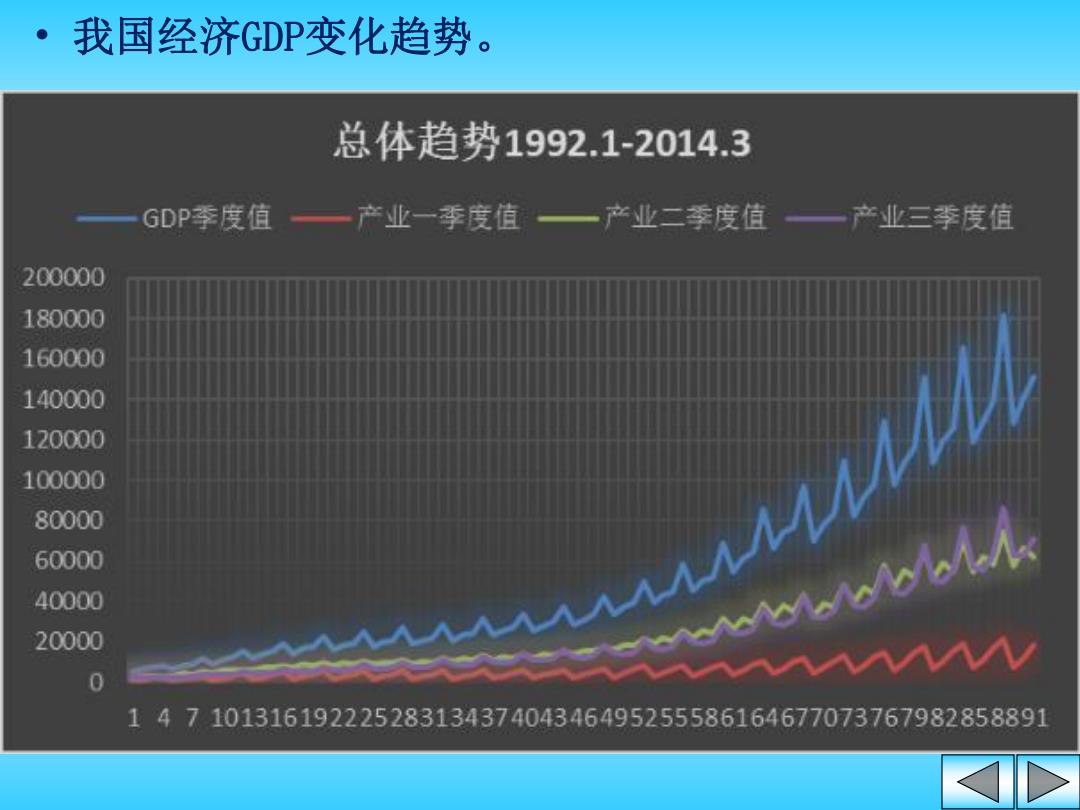
·我国经济GDP变化趋势。 总体趋势1992.1-2014.3 GDP季度值一产业一季度值一产业二季度值一产业三季度值 200000 180000 160000 140000 120000 100000 80000 60000 40000 20000 0 14710131619222528313437404346495255586164677073767982858891
• 我国经济GDP变化趋势

现象特点:关注一族随时间或地,点变 化的随机变量,有自身的统计规律,而 且变量间有着内在的关联关系. 随机过程论:研究和描述随机现象演变 的概率统计规律. 随机过程理论是近代数学的重要组成部 分,应用非常广泛,实际工程背景强
随机过程论:研究和描述随机现象演变 的概率统计规律. 现象特点:关注一族随时间或地点变 化的随机变量,有自身的统计规律,而 且变量间有着内在的关联关系. 随机过程理论是近代数学的重要组成部 分, 应用非常广泛,实际工程背景强

二、研究方法 Ex.设某种细菌群体的个数在时段(,什△)内 只能增加,增加的数量与t时刻的细菌数成正比, 且x=x(0)>0. 1)确定性方法设t时刻的细菌数为x(),有 △x(t)=入x(t)△t, (入>0). 令△t→0得微分方程 dx(1)=Xx(t) dt 解得实值连续函数x(t)=xe“,t≥0
Ex. 设某种细菌群体的个数在时段(t, t+Δt)内 只能增加,增加的数量与t 时刻的细菌数成正比, 且x0 =x(0)>0. 1) 确定性方法 设t 时刻的细菌数为x(t),有 x(t) x(t)t, ( 0). ( ) d ( ) x t dt x t 二、研究方法 解得实值连续函数 ( ) , 0. x t x0e t t