
§3.1正态过程 在现实问题中,满足一定条件的随机变量 之和的极限服从正态分布. 电子技术中的热噪声是由大量的热运动引 起,也服从正态分布. 由于一个随机过程可以用有限维分布来 描述,为研究正态过程应首先研究多维正态分 布随机变量. 电子科技大学
电子科技大学 §3.1 正 态 过 程 在现实问题中,满足一定条件的随机变量 之和的极限服从正态分布. 电子技术中的热噪声是由大量的热运动引 起,也服从正态分布. 由于一个随机过程可以用有限维分布来 描述,为研究正态过程应首先研究多维正态分 布随机变量

多维正态随机变量 1.概率密度与特征函数 若(X,)~N(1,o;u2,o2;p) X,)的联合概率密度为 p(x,y)= X 2πg02V1-p2 mn-。.5 01 电子科技大学
电子科技大学 一、多维正态随机变量 1.概率密度与特征函数 (X,Y)的联合概率密度为 2 2 1 2 1 ρ 1 ( , ) x y 2 2 1 1 2 2 2 2 2 1 1 2 2 1 ( ) ( ) ( ) ( ) exp 2ρ 2(1 ) x x y y

记 = 时 E X= p012 其中01>0,02>0, |pK1,故协方差 矩阵满足B卡0
电子科技大学 记 , ( ) ( ) 2 1 μ μ μ E Y E X Y X E 2 1 2 2 1 2 2 1 B y x X 其中σ1>0,σ2>0, | |<1, 故协方差 矩阵满足|B|≠0

(X,)的联合概率密度为 o(x,y)= X 2πgo2V1-p2 a-aw,“ 01 02 网时 记为X,)N(u,B). 电子科技大学
电子科技大学 (X,Y)的联合概率密度为 2 1 2 2 1 1 ( , ) ρ x y 2 2 1 1 2 2 2 2 2 1 1 2 2 1 ( ) ( ) ( ) ( ) exp 2 2(1 ) x x y y ( μ) τ ( μ) 2 1 exp 2π 1 1 2 1 X B X B

定义3.1.1设B=(b)是n阶正定对称矩阵,u是 n维实值列向量,定义n维随机向量 X=(XI X2...,X) 的联合密度函数为 f(x1,x2,,xm)= 1 p-n以-叫o 2m 其中X=(x,x2,,x),称X服从n维正态分布. 电子科技大学
电子科技大学 定义3.1.1 设B=(bij) 是n 阶正定对称矩阵,μ是 n 维实值列向量, 定义n维随机向量 X=(X1 , X2 , …, Xn ) t 的联合密度函数为 f x1 , x2 ,, xn 1 1 2 2 1 1 τ exp ( μ) ( μ) 2 (2π) X X n B B (*)

记为X=X1,X2,,Xn)TN(u,B). 注当B=(b)是阶正定对称矩阵,有引B1≠0 若引B引=0则不能用(*)式给出其概率密度. 定理3.1.1n维正态分布随机向量X=(X,X, ,X)的特征函数为 w)-op'u-w 其中u=(u1,u2,…,un)7. 电子科技大学
电子科技大学 注 定理3.1.1 n维正态分布随机向量X=(X1 , X2 , …, Xn ) 的特征函数为 (**)

定义3.1.2若u是n维实向量,B是n阶非负 定对称阵,称以(**)式中的φ()为其特征函数 的n维随机变量X服从n维正态分布。 注若(**)式中的B!=0,称X服从退化正态分 布或奇异正态分布. 2.边缘分布及二阶矩 以下结论总假定随机向量X=(X,X2,,X,)T 服从N(,B). 电子科技大学
电子科技大学 定义3.1.2 若μ是n 维实向量, B 是n 阶非负 定对称阵, 称以(**)式中的 为其特征函数 的n 维随机变量X 服从n 维正态分布. (t) 2.边缘分布及二阶矩

定理3.1.2n维正态分布随机变量X的任一 子向量 (XXXk) (m≤n) 也服从正态分布B(元,B),其中 a=(uk1uk2,…,km),B是B保留第k,k2,, k,m行及列所得的m阶矩阵. 多元正态分布的 边缘分布仍是正 态分布 电子科技大学
电子科技大学 定理3.1.2 n维正态分布随机变量X的任一 子向量 ( , , , ) ( ) τ 1 2 X X X m n k k km 多元正态分布的 边缘分布仍是正 态分布
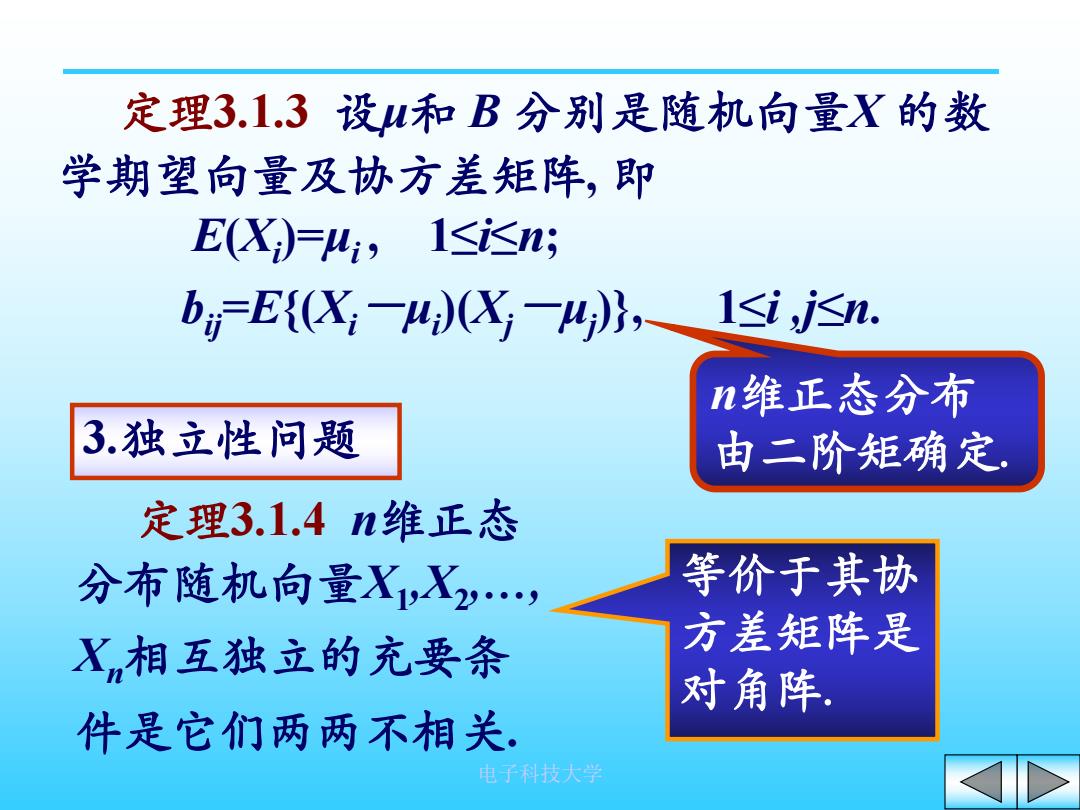
定理3.1.3设u和B分别是随机向量X的数 学期望向量及协方差矩阵,即 E(X)=4,1≤isn; b,E{X:一X一4},1≤i,jn. n维正态分布 3.独立性问题 由二阶矩确定 定理3.1.4n维正态 分布随机向量X,X, 等价于其协 X相互独立的充要条 方差矩阵是 对角阵。 件是它们两两不相关 电子科技大学
电子科技大学 定理3.1.3 设μ和 B 分别是随机向量X 的数 学期望向量及协方差矩阵, 即 E(Xi)=μi , 1≤i≤n; bij =E{(Xi-μi)(Xj-μj)}, 1≤i ,j≤n. n维正态分布 由二阶矩确定. 3.独立性问题 定理3.1.4 n维正态 分布随机向量X1 ,X2 ,…, Xn相互独立的充要条 件是它们两两不相关. 等价于其协 方差矩阵是 对角阵

4.正态随机向量的线性变换 定理3.1.5正态随机向量X=(XvX…,Xm)T, 记E()=山,协方差矩阵为B. 1)对X的线性组合 7=∑,X,=LX,L=4,2,,ln) i=1 有 EY)=1,4,=L, D)=∑2H,=LB,, i=1k=1 电子科技大学
电子科技大学 4.正态随机向量的线性变换 定理3.1.5正态随机向量 X=(X1 ,X2 ,…,Xn ) τ , 记E(X)=μ, 协方差矩阵为B. 1 , n j j j Y l X LX L=(l1 , l2 ,…, ln ) 有 1 1 τ ( ) , n n j k jk j k D Y l l b LBL 1 ( ) μ, n j j j E Y l L 1) 对X 的线性组合