
随机过程的分布 04.9.4 §2.2随机过程的分布 、分布函数 定义2.2.1随机过程Xx={X(t),t∈T},对 Vt∈T,随机变量X(t)的分布函数 Ft;x)=P{Xt)≤x},x∈R 称为过程X,的一维分布函数, 注 一维分布函数描述了随机过程在各个孤 立时间,点处的统计特性,未给出过程的整体 统计特性, 电子科技大学
随机过程的分布 04.9.4 电子科技大学 §2.2 随机过程的分布 一、分布函数 称为过程XT的一维分布函数. 注 一维分布函数描述了随机过程在各个孤 立时间点处的统计特性, 未给出过程的整体 统计特性. F(t; x) = P{ X(t) ≤ x }, x∈R

随机过程的分布 04.9.4 E 定义2.2.2 随机过程{X(t),t∈T),对任给的 t1,t2,…,tn∈T,随机向量 (X(1),X(t2),…,X(tn) 的联合分布函数 F(G1,t2,…,tnK1,x2,…,xn≌ P{X(t1)≤x1,X(t)≤X2,…,X(n)≤xn} 称为过程的n维分布函数. 电子科技大学
随机过程的分布 04.9.4 电子科技大学 ( ), ( ), , ( ) 1 2 n X t X t X t 的联合分布函数 称为过程的n 维分布函数. 1 2 1 2 ( , , , ; , , , ) F n n t t t x x x 1 1 2 2 { ( ) , ( ) , , ( ) } P X n n t x X t x X t x

随机过程的分布 04.9.4 记F兰{F(t1,t2)…,t;X1,2,xn): t;∈T,x∈R,i=1,2,…,n,n≥1} 称F为X,的有限维分布函数族」 Xx的任意有 限维分布函 数的全体构 成的集合 定义2.2.3过程{X(t),t∈T)的n维特征函数定 义为 p(t1,t2,…,tn;01,02,…,0n)= 电子科技大学
随机过程的分布 04.9.4 电子科技大学 , , 1,2, , , 1} F ˆ { ( , , , ; , , , ): 1 2 1 2 t T x R i n n F t t t x x x i i i n n 称F为XT的有限维分布函数族. XT的任意有 限维分布函 数的全体构 成的集合 φ(t1 ,t2 ,,tn;θ1 ,θ2 ,,θn ) 记

随机过程的分布 04.9.4 =E{e8,xG++8mx(.川小} 称 {0(t1,t2,…,tn01,02,…,0n): t1,t2,…,tn∈T,n≥1} 为X,的有限维特征函数族 特征函数和分布函数是相互唯一确定, 2.随机过程存在定理 随机过程的维分布函数能近似地描述 过程的统计特性,n越大则描述越趋于完善, 电子科技大学
随机过程的分布 04.9.4 电子科技大学 { } [θ ( ) θ ( )] 1 1 n n j X t X t E e 特征函数和分布函数是相互唯一确定. , , , , 1} {φ( , , , ;θ ,θ , ,θ ): 1 2 1 2 n 1 2 t t t T n t t t n n 称 为XT的有限维特征函数族. 2. 随机过程存在定理 随机过程的n维分布函数能近似地描述 过程的统计特性, n越大则描述越趋于完善

随机过程的分布 04.9.4 需研究随机过程与有限维分布函数的关系, 随机过程的有限维分布函数有以下性质: 1)对称性:对1,2,,n的任一排列j1,j2,…, jn,均有 F(tiy…,t,火iy…,xin)=F(41,42,…,tnx1,X2,xn) 注 因事件乘积满足交换律 2)相容性:对任意固定的自然数n,均有 F(41,t2,…,tm;X1,x2,,xm) 电子科技大学
随机过程的分布 04.9.4 电子科技大学 F t1 ,t2 ,,tm ; x1 , x2 ,, xm 需研究随机过程与有限维分布函数的关系. 随机过程的有限维分布函数有以下性质: 1) 对称性:对1, 2, …, n的任一排列j1 , j2 , … , jn ,均有 ( , , ; , , ) ( , , , ; , , , ) 1 2 1 2 j1 j j1 j n n F t t x x F t t t x x x n n 注 因事件乘积满足交换律. 2) 相容性:对任意固定的自然数m<n,均有

随机过程的分布 04.9.4 =F(t1,t2,…,tm,…,tnX1,2…3火m30.oo) limF(t1,t2…,tn1,xm,…xn) 尤m+1,,n→00 注 联合分布函数能完全确定边缘分布函数 类似地,随机过程的有限维特征函数满足: 1)对1,2,,n的任一排列j1,j2,,jn有 0(iy…,401y…,0.)=p(41,42,…,tn;01,02,…,0n) 2)对任意固定的自然数m<n,均有 电子科技大学
随机过程的分布 04.9.4 电子科技大学 ( , , , , , ; , , , , ) F t1 t2 tm tn x1 x2 xm lim ( , , , ; , , , ) 1 2 1 , , 1 n m n x x F t t t x x x m n 注 联合分布函数能完全确定边缘分布函数. 类似地,随机过程的有限维特征函数满足: 1) 对1,2,…,n的任一排列j1 , j2 , …, jn有 ( , , ;θ , ,θ ) ( , , , ;θ ,θ , ,θ ) 1 2 1 2 j1 j j1 j n n φ t t φ t t t n n 2) 对任意固定的自然数m<n,均有

随机过程的分布 04.9.4 p(t1,2,…,tm01,023…,0m) =0(t1,t2y…,tm)…,tn;01,02)…,0m,0,…,0) 定理2.2.1(柯尔莫哥罗夫存在定理) 如果有限分布函数族 F={F(41,t2,…,tn;X1,x2,,xn)t1,t2,…,tn∈T,n≥1l 满足相容性和对称性,则存在一个概率空间上 的一个随机过程Xr=X(t),t∈T以F为有限维 分布函数族,即 电子科技大学
随机过程的分布 04.9.4 电子科技大学 XT X(t),t T φ( , , , ;θ ,θ , ,θ ) 1 2 m 1 2 m t t t φ( , , , , , ;θ ,θ , ,θ ,0, ,0) t1 t2 tm tn 1 2 m 定理2.2.1 (柯尔莫哥罗夫存在定理) 如果有限分布函数族 F { ( , , , ; , , , ), , , , , 1} F t1 t2 tn x1 x2 xn t1 t2 tn T n 满足相容性和对称性,则存在一个概率空间上 的一个随机过程 以F 为有限维 分布函数族, 即

随机过程的分布 04.9.4 F(t1,t2,…,tnX13x2,3n) =P{X(t1)≤X1,…,X(tn)≤xn}. Ex1.设随机过程{X(t,o),t∈R只有两条样本 函数 X(t,@)=2cost,X(t,0,)=-2cost,tER 且 P(o Pe 求1)一维分布函数F(0;x)和F(/4;x); 2)二维分布函数F(0,/4;飞,y). 电子科技大学
随机过程的分布 04.9.4 电子科技大学 ( , , , ; , , , ) 1 2 n x1 x2 xn F t t t 1 1 { ( ) , , ( ) }. P X n n t x X t x Ex1.设随机过程 只有两条样本 函数 X(t,),t R X(t,1 ) 2cost, X(t,2 ) 2cost, t R 且 1 2 2 1 {ω } , {ω } 3 3 P P 求 1) 一维分布函数F(0; x) 和 F(p/4; x); 2) 二维分布函数F(0, p/4; x, y)

随机过程的分布 04.9.4 解1)对任意实数t∈R,有 X(t) -2cost 2cost p 1/3 2/3 特别 -2 2 1/3 2/3 √2 p 1/3 2/3 电子科技大学
随机过程的分布 04.9.4 电子科技大学 解 1) 对任意实数t∈R,有 X(t) - 2cost 2cost p 1/3 2/3 特别 X(0) - 2 2 p 1/3 2/3 X( ) p 1/3 2/3 2 2 4 p
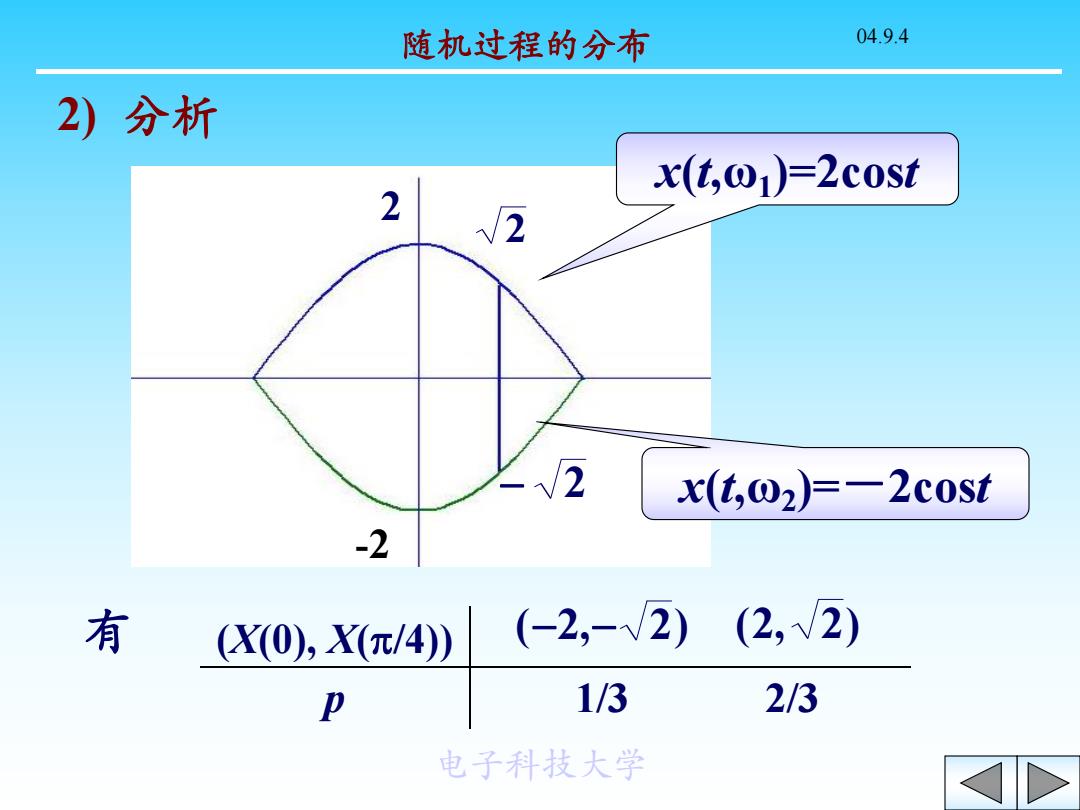
随机过程的分布 04.94 2)分析 x(t,@)=2cost 2 2 2 x(t,02)=-2cost -2 有 (X0),X元/4) (-2,-V2)(2,V2) 1/3 2/3 电子科技大学
随机过程的分布 04.9.4 电子科技大学 2) 分析 有 (X(0), X(p/4)) p 1/3 2/3 (2, 2) (2, 2) x(t,ω1)=2cost x(t,ω2)=-2cost 2 2 -2 2