
§6.3齐次马氏链状态的分类(一) 为揭示齐次马氏链的基本结构,需对其状 态按某些概率特性进行分类,状态分类是研 究n步转移概率的极限状态的基础. 状态类型定义 EX.1设系统有三种可能状态E={1,2,3}, “1”表示系统运行良好,“2”表示系统运行正 常,“3”表示系统失败. 电子科技大学
电子科技大学 §6.3 齐次马氏链状态的分类(一) 为揭示齐次马氏链的基本结构,需对其状 态按某些概率特性进行分类,状态分类是研 究n步转移概率的极限状态的基础. 一、状态类型定义 EX.1 设系统有三种可能状态E={1, 2 ,3}, “1”表示系统运行良好, “2”表示系统运行正 常, “3”表示系统失败

以X(n)表示系统在n时刻的状态,并设 X(m),n20}是一马氏链.在没有维修及更换 的条件下,其自然转移概率矩阵为 2 p11 P12 P13 20 20 20 P= P21 P22 P23 0 10 P31 p32 p33 0 0 由矩阵P可见,从“1”或“2”出发经有限次 转移后总能到达“3”状态,而一旦到达“3” 状态则永远停留在“3”. 电子科技大学
电子科技大学 以X(n)表示系统 在n 时刻的状态, 并设 {X(n),n≥0}是一马氏链. 在没有维修及更换 的条件下, 其自然转移概率矩阵为 0 0 1 10 1 10 9 0 20 1 20 2 20 17 31 32 33 21 22 23 11 12 13 p p p p p p p p p P 由矩阵P可见,从“1”或“2”出发经有限次 转移后总能到达“3”状态,而一旦到达“3” 状态则永远停留在“3

状态“1”,“2”与状态“3”有不同的概率特性. 1.刻画状态特性的几个特征量 定义6.3.1对Vi,j∈E及n≥2,记 f盼会PX四=K(0)= f分会PXm)=j方,X)≠j,k=1,2,,n-1K0)=i 称为(n步)首达概率 系统从状态“” 出发经过n步转 称f)=∑f”为最终概率。 移后首次到达状 n=1 态“”的概率 电子科技大学
电子科技大学 状态“1” , “2”与状态“3”有不同的概率特性. 1. 刻画状态特性的几个特征量 定义6.3.1 对i, j E 及 n 2,记 ˆ { (1) (0) } (1) f P X j X i ij ˆ { ( ) , ( ) , 1,2, , 1 (0) }, ( ) f P X n j X k j k n X i n ij 称为(n步)首达概率. 1 ( ) n n ij ij 称 f f 为最终概率. 系统从状态“i” 出发经过n步转 移后首次到达状 态“j” 的概率

最终概率 f=P{存在n≥1,使X(m)=jX(0)=i, 是系统从状态“”出发经过有限步转移后 最终到达状态“”的概率. 定理6.3.1 首达概率表示式 对Vi,j∈E及n≥l,有 )0≤分≤15 2)首达概率可以用一步转移概率表示为 电子科技大学
电子科技大学 f P{ n 1, X(n) j X(0) i}, ij 存在 使 是系统从状态“i” 出发经过有限步转移后 最终到达状态“j” 的概率. 最终概率 定理6.3.1 首达概率表示式 对i, j E 及 n 1,有 1) 0 1; ( ) n ij f 2)首达概率可以用一步转移概率表示为
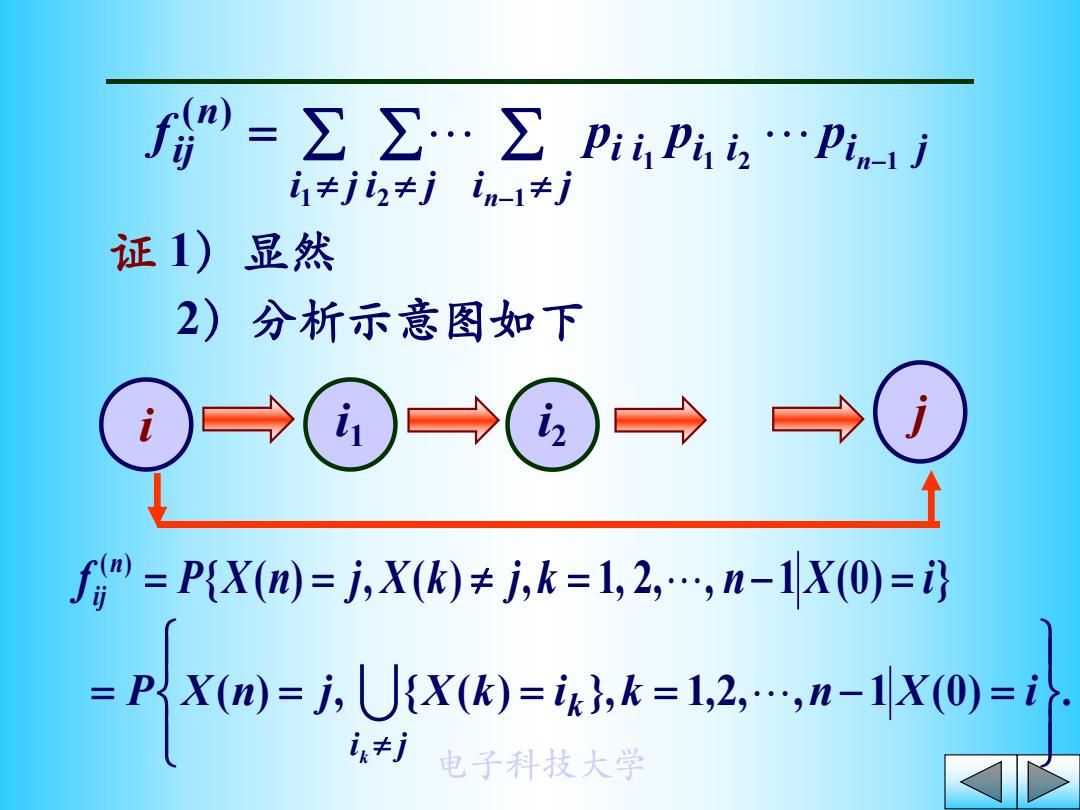
f}=∑∑…∑Pi,Pi,Pn1j 1≠j2≠jin-1≠j 证1)显然 2)分析示意图如下 i j f分=P{X(m=j,X(k)≠j,k=1,2,,n-1X0)=i =Xm=X=k=28-0= i,j电子科技大学
电子科技大学 i i i j i j i j i i i j n ij n n f p p p 1 2 1 1 1 1 2 ( ) 证 1)显然 i i1 i2 j 2)分析示意图如下 { ( ) , ( ) , 1, 2, , 1 (0) } ( ) f P X n j X k j k n X i n ij ( ) , { ( ) }, 1,2, , 1 (0) . P X n j X k i k n X i i j k k

=4=心w=4=2a-x= -UU-Ug itjij itj =∑∑:…∑PX=i,,Xm-0=in-,X四=jX0=i i1≠ji2+jin-1tj =∑∑…∑PiP话,…Pij i≠j2+jin1*j 电子科技大学
电子科技大学 P X i X n i X n j X i n i j i j i j n { (1) , , ( 1) , ( ) } (0) 1 1 1 2 1 ( ) , { ( ) }, 1,2, , 1 (0) . P X n j X k i k n X i i j k k i j i j i j 1 2 n 1 { (1) , , ( 1) , ( ) (0) } 1 1 P X i X n i X n j X i n i i i j i j i j ii i j n n p p p 1 2 1 1 1 1 2

定义63.2对i∈E,称 T=min{n:n≥1,X(n)=j,X(0)=i} 为到达j的首达时间. 随机变量 注若右边是空集,则令T0. EX.2在股票交易过程中令状态空间为 E={-1,0,1} 各状态分别代表“下跌”、“持平”、“上升” 若X(0)=0,有h1<n2<…<<…使 电子科技大学
电子科技大学 定义6.3.2 对j∈E, 称 T min{n : n 1, X(n) j, X(0) i} ij 为到达 j 的首达时间. 注 若右边是空集, 则令Tij=∞. 随机变量 EX. 2 在股票交易过程中令状态空间为 E={-1, 0, 1} 各状态分别代表“下跌” 、 “持平” 、 “上升” , 若X(0)=0, 有 n1 n2 nk 使

X(n1)=1,X(2)=1,…,X(nk)=1,… to minfn:X(nx)=1,X(0)=0) =min{1,2,…,nk,}=n1 注1 T:表示从i出发首次到达j的时间, T表示从i出发首次回到i的时间. 注2 T与首达概率之间有关系式: 1) f=P(Ty nlx(0)=0ij EE,n=1,2,... 2)fi=P{Ti<0X(0)=i, i,ieE. 电子科技大学
电子科技大学 X(n1 ) 1, X(n2 ) 1,, X(nk ) 1, min{ : ( ) 1, (0) 0} 则 t01 n X nk X 1 2 1 min{n ,n ,,nk ,} n 注 1 Tij表示从 i 出发首次到达 j 的时间, Tii表示从 i 出发首次回到i 的时间. 注 2 Tij与 首达概率之间有关系式: 2) f P{T X(0) i}, i, j E. ij ij

续X.1设系统有三种可能状态E={1, 2,3},“1”表示系统运行良好,“2”表示系统运 行正常,“3”表示系统失败 P11 P12 P13 [1720 20 20 P= 0 p21 P22 P23 三 10 P31 P32 p33 0 0 1 T13是系统的工作寿命,有 f8=P{T13=1X(0)=1=P13= 1 20 电子科技大学
电子科技大学 续EX.1 设系统有三种可能状态E={1, 2 ,3}, “1”表示系统运行良好, “2”表示系统运 行正常, “3”表示系统失败. 0 0 1 10 1 10 9 0 20 1 20 2 20 17 31 32 33 21 22 23 11 12 13 p p p p p p p p p P T13是系统的工作寿命,有 , 20 1 { 1 (0) 1} 13 13 (1) 13 f P T X p

f8=PT13=2X(0)=1 21 =P11P13+P12P23= 4002 P{T13≥n}是系统在[0,n]内运行的可靠性,有 00 PT3≥m=∑PTg=kXo)=1刂=∑f格 k=n k=n 研究首达概率和首达时间有实际工程意义, 电子科技大学
电子科技大学 , 400 21 { 2 (0) 1} 11 13 12 23 13 (2) 13 p p p p f P T X 研究首达概率和首达时间有实际工程意义. ……