
优化试验设计与数据分析 第二章方差分析方法 cmese,uestc 本章主要内容 一、试验数据构造模型 二、正交试验的方差分析法 三、有重复试验的方差分析 四、缺落数据的弥补 School of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 优化试验设计与数据分析 本章主要内容 · 一、试验数据构造模型 · 二、正交试验的方差分析法 · 三、有重复试验的方差分析 · 四、缺落数据的弥补

第二章方差分析方法 >在工农业生产和科研活动中, 我们经常遇到这样 的问题:影响产品产量、质量的因素很多,例如影 响农作物的单位面积产量有品种、施肥种类、施肥 量等许多因素。我们要了解这些因素中哪些因素对 产量有显著影响,就要先做试验,然后对测试结果 进行分析,作出判断。方差分析是分析测试结果的 种方法。 Schodl of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 ➢ 在工农业生产和科研活动中,我们经常遇到这样 的问题:影响产品产量、质量的因素很多,例如影 响农作物的单位面积产量有品种、施肥种类、施肥 量等许多因素。我们要了解这些因素中哪些因素对 产量有显著影响,就要先做试验,然后对测试结果 进行分析,作出判断。方差分析是分析测试结果的 一种方法

第二章方差分析方法 >正交试验方差分析的意义 >极差分析法的优点是简单明了、通俗易懂、计算 工作量少、便于普及推广。 >缺点是 cmese.uestc ①极差分析法不能把试验中由于试验因素的改变引起的 数据波动同试验误差引起的数据波动区别开来。 ②极差分析法对影响试验结果的各因素的重要程度,不 能给以精确的数量估计,不能判断考察因素的作用是否 显著。 Schodl of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 ➢正交试验方差分析的意义 ➢极差分析法的优点是简单明了、通俗易懂、计算 工作量少、便于普及推广。 ➢缺点是: – ①极差分析法不能把试验中由于试验因素的改变引起的 数据波动同试验误差引起的数据波动区别开来。 – ②极差分析法对影响试验结果的各因素的重要程度,不 能给以精确的数量估计,不能判断考察因素的作用是否 显著

第二章方差分析方法 >方差分析(analysis of variance)是数理统 计的基本方法之一,是工农业生产和科研上 分析试验数据的一种有效工具。 cmese.uestc >它所要解决的基本问题是 >通过数据分析,搞清与实验研究有关的各 个因素对实验结果的影响及影响的程度,即 对实验结果有无显著性影响的问题。 School of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 ➢方差分析(analysis of variance)是数理统 计的基本方法之一,是工农业生产和科研上 分析试验数据的一种有效工具。 ➢它所要解决的基本问题是: ➢通过数据分析,搞清与实验研究有关的各 个因素对实验结果的影响及影响的程度,即 对实验结果有无显著性影响的问题
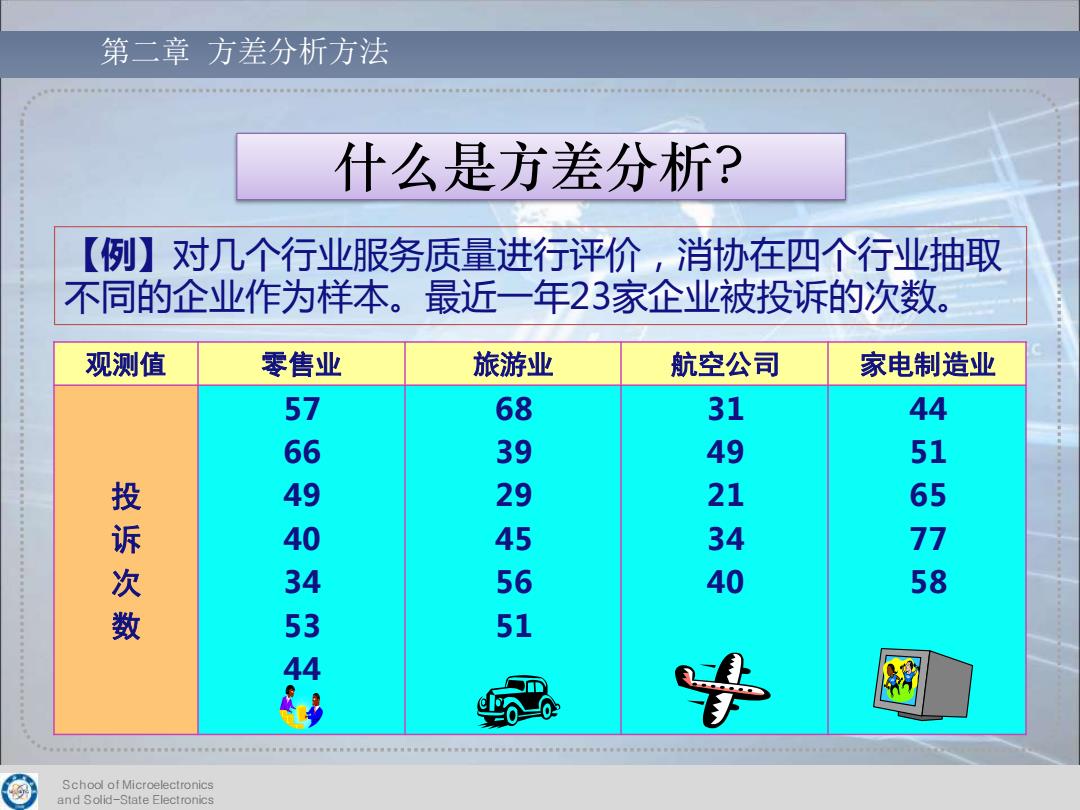
第二章方差分析方法 什么是方差分析? 【例】对几个行业服务质量进行评价,消协在四个行业抽取 不同的企业作为样本。最近一年23家企业被投诉的次数。 观测值 零售业 旅游业 航空公司 家电制造业 5 31 44 6 49 21 5 投诉次数 4 3 689294451 40 78 53 4 School of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 什么是方差分析? 观测值 零售业 旅游业 航空公司 家电制造业 投 诉 次 数 57 66 49 40 34 53 44 68 39 29 45 56 51 31 49 21 34 40 44 51 65 77 58 【例】对几个行业服务质量进行评价,消协在四个行业抽取 不同的企业作为样本。最近一年23家企业被投诉的次数

第二章方差分析方法 什么是方差分析?(例题分析) 1. 分析四个行业之间的服务质量是否有显著差异 也就是要判断“行业”对“投诉次数”是否有显 著影响 cmese.uesto 2.作出这种判断最终被归结为检验这四个行业被投 诉次数的均值是否相等 3. 若它们的均值相等,则意味着“行业”对投诉次 数是没有影响的,即它们之间的服务质量没有显 著差异;若均值不全相等,则意味着“行业”对 投诉次数是有影响的,它们之间的服务质量有显 著差异 Schodl of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 什么是方差分析?(例题分析) 1. 分析四个行业之间的服务质量是否有显著差异, 也就是要判断“行业”对“投诉次数”是否有显 著影响 2. 作出这种判断最终被归结为检验这四个行业被投 诉次数的均值是否相等 3. 若它们的均值相等,则意味着“行业”对投诉次 数是没有影响的,即它们之间的服务质量没有显 著差异;若均值不全相等,则意味着“行业”对 投诉次数是有影响的,它们之间的服务质量有显 著差异

第二章方差分析方法 方差分析的基本思想和原理 80 60 40 20 零售业 旅游业 航空公司家电制造 1 2 3 4 5 不同行业被投诉次数的散点图 行业 Schodl of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 方差分析的基本思想和原理 不同行业被投诉次数的散点图 0 20 40 60 80 0 1 2 3 4 5 行业 被投诉次数 零售业 旅游业 航空公司 家电制造

第二章方差分析方法 >从散点图上可以看出 - 不同行业被投诉的次数是有明显差异的 ·家电制造被投诉的次数较高,航空公司被投诉的次数较低 一同行业的不同企业被投诉的次数也明显不同 cmese.uestc >仅从散点图上观察还不能提供充分的证据证明不 同行业被投诉的次数之间有显著差异 一这种差异也可能是由于抽样的随机性所造成的 Schodl of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 ➢从散点图上可以看出 – 不同行业被投诉的次数是有明显差异的 • 家电制造被投诉的次数较高,航空公司被投诉的次数较低 – 同行业的不同企业被投诉的次数也明显不同 ➢仅从散点图上观察还不能提供充分的证据证明不 同行业被投诉的次数之间有显著差异 – 这种差异也可能是由于抽样的随机性所造成的

第二章方差分析方法 方差分析的基本思想和原理 需要有更准确的方法来检验这种差异是否 显著,也就是进行方差分析 所以叫方差分析,因为虽然我们感兴趣的是 均值,但在判断均值之间是否有差异时则需 要借助于方差 这个名字也表示:它是通过对数据误差来源 的分析判断不同总体的均值是否相等。因此 进行方差分析时,需要考察数据误差的来 源 Schodl of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 方差分析的基本思想和原理 需要有更准确的方法来检验这种差异是否 显著,也就是进行方差分析 – 所以叫方差分析,因为虽然我们感兴趣的是 均值,但在判断均值之间是否有差异时则需 要借助于方差 – 这个名字也表示:它是通过对数据误差来源 的分析判断不同总体的均值是否相等。因此 ,进行方差分析时,需要考察数据误差的来 源

第二章方差分析方法 两类误差 1。随机误差 因素的同一水平(总体)下,样本各观察值之间 的差异 ◆比如,同一行业下不同企业被投诉次数是不同的 这种差异可以看成是随机因素的影响,称为随 机误差 Schodl of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 第二章 方差分析方法 两类误差 1. 随机误差 ▪ 因素的同一水平(总体)下,样本各观察值之间 的差异 ◆ 比如,同一行业下不同企业被投诉次数是不同的 ▪ 这种差异可以看成是随机因素的影响,称为随 机误差