
分段插值 分段插值函数 三次样条插值的概念 用一阶导数表示的样条 三次样条的极性 二元函数插值简介
1 分段插值函数 三次样条插值的概念 用一阶导数表示的样条 三次样条的极性 二元函数插值简介 分段插值

分段线性插值 插值节点满足:X<x<<Xm己知 yf(c) (j=0,1,2,…,n) x∈[比+时,线性插值函数 Ln()=七i+1r y+ x-xi-yi (j=0,1,…,n-1) 2
2 分段线性插值 插值节点满足: x0<x1<······<xn 已知 yj=f (xj) ( j= 0,1,2,···,n) 1 1 1 1 ( ) j j j j j j j j h y x x x x y x x x x L x ( j= 0,1,···,n-1) x∈[xj,xj+1]时, 线性插值函数

分段线性插值 yt Xo Xj-1 Xj Xj+1 Xn X Ln(x)=∑yl,(x) x-xL,x-1≤x≤xj 计算量与n无关; xj-xj-1 X-,x,≤x≤x n越大,误差越小. L,(x)= xj-xj+1 0, 其它 limL.(x)=g(x),x≤x≤xm n-00 3
3 分段线性插值 计算量与n无关; n越大,误差越小. n n n L x g x x x x 0 lim ( ) ( ), x0 xj-1 xj xj+1 xn x o y 0 , 其它 , , ( ) ( ) ( ) 1 1 1 1 1 1 0 j j j j j j j j j j j n j n j j x x x x x x x x x x x x x x l x L x y l x
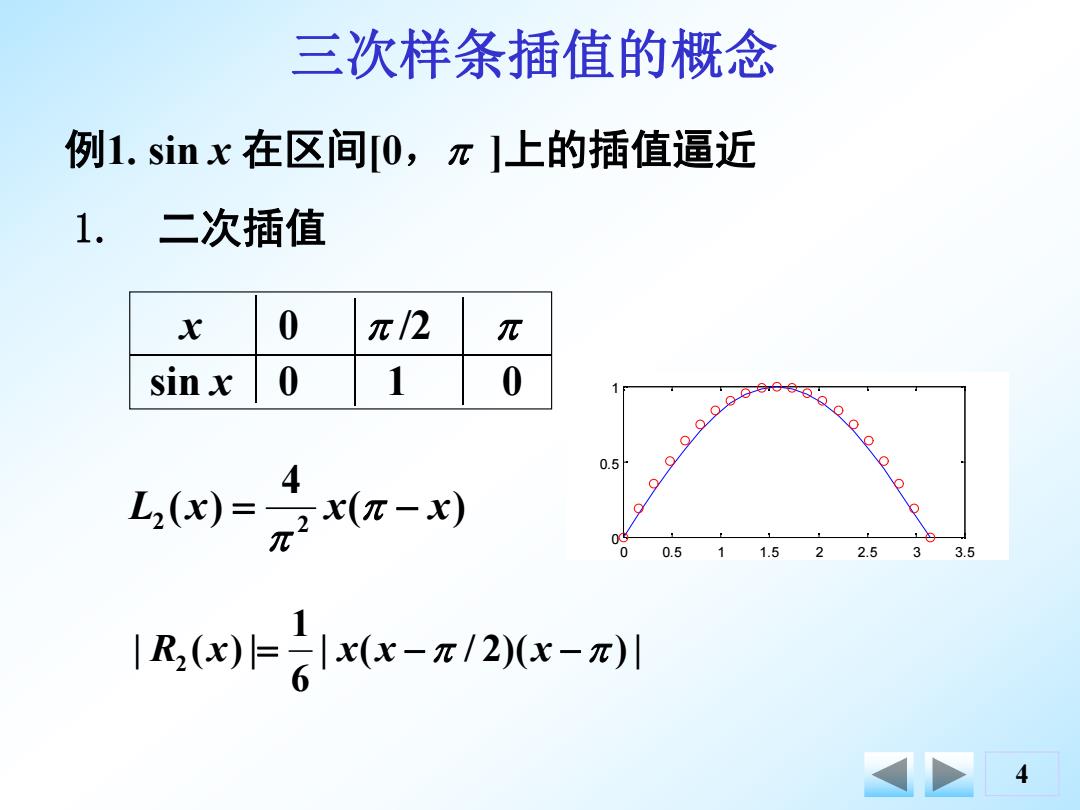
三次样条插值的概念 例1.sinx在区间[0,π]上的插值逼近 1.二次插值 X 0 π/2 π sin x 0 1 0 0.5 4 L,()=元π- 0 0.5 1.5 2 2.5 33.5 IR,(x)非言x-π12-川 4
4 例1. sin x 在区间[0, ]上的插值逼近 1. 二次插值 0 0.5 1 1.5 2 2.5 3 3.5 0 0.5 1 x 0 /2 sin x 0 1 0 ( ) 4 ( ) 2 2 L x x x | ( / 2)( )| 6 1 | ( )| R2 x x x x 三次样条插值的概念

定义5.4给定区间[a,b]上的一个分划: a=x<x<...<x=6 己知x)=y0=0,1,…,,如果 S1(x),x∈[xo,x1] S(x)= S2(x),x∈x1,x2] Sn(x),x∈[xm-1xnJ 满足:(I)Sx)在比?x#上为三次多项式; (2)Sx)在区间[M,b]上连续; (3)Sc)=y;(j=0,1,…,n). 则称S)为三次样条插值函数. 5
5 定义 5.4 给定区间[a , b]上的一个分划: a = x0 < x1 < … < x n = b 已知 f(xj) = yj (j = 0,1,···,n), 如果 ( ), [ , ] ( ), [ , ] ( ), [ , ] ( ) 1 2 1 2 1 0 1 n n n S x x x x S x x x x S x x x x S x 满足: (1) S(x)在 [xj,xj+ 1]上为三次多项式; (2) S”(x)在区间[a,b]上连续; (3) S(xj) = yj ( j = 0,1,···,n). 则称 S(x)为三次样条插值函数

n个三次多项式,待定系数共4n个! 当x∈s,#l(j=0,1,.m-1)时 Sx)=aj+bix+cix2+dix3 插值条件:Sc)=y(j=0,1,…,n) 连续性条件:Sc+0)=S(c0) (j=1,…,n-1) S'(c0)=S(c0)(j=1,…,n-1) S”(ct0)=S”(c0)(j=1,,n-1) 由样条定义,可建立方程(4n-2)个! 方程数少于未知数个数?? 6
6 当x∈[xj , xj+ 1] ( j= 0,1,…n-1 )时 Sj(x)= aj + bj x + cj x 2 + dj x 3 插值条件: S(xj) = yj ( j = 0,1,···,n) 连续性条件: S(xj+0) =S(xj-0) ( j = 1,···,n-1) S’(xj+0) =S’(xj-0) ( j = 1,···,n-1) S”(xj+0) =S”(xj-0) ( j = 1,···,n-1) 由样条定义,可建立方程(4n-2)个! n个三次多项式, 待定系数共4n个! 方程数少于未知数个数 ??

(1)自然边界条件:S”x)=0,S”比n)=0 (2)周期边界条件:S'xo)=S'K),S”(xo)=S"xm) 3)固定边界条件:S'()=f'x),S'(Km)=f'化n) 例25.7已知f-1)=1,f0)=0,1)=1.求-1,1]上 的三次自然样条(满足自然边界条件). 解设 ax3+bx2+cix+d x∈[-1,0] S(x)= a,x3+bc2+cx+d,x∈0,1刂 则有: -a1+b1-c1+d1=1, d1=d2, d=0, 1 C1-C2, a2+b2+C2+l2=1 b1-b2
7 (1)自然边界条件: S”(x0)=0, S”(xn )=0 例2 5.7 已知f(–1) = 1, f(0) = 0, f(1) = 1.求[–1,1]上 的三次自然样条(满足自然边界条件). 解 设 , [ , ] , [ , ] ( ) 0 1 1 0 2 2 2 2 3 2 1 1 2 1 3 1 a x b x c x d x a x b x c x d x S x 则有: – a1+b1–c1+d1 =1, d1 =0, a2+b2+c2+d2 =1 (2)周期边界条件: S’(x0)=S’(xn ), S”(x0)=S”(xn ) (3)固定边界条件: S’(x0)=f ’(x0), S’(xn )=f ’(xn ) d1=d2 , c1 =c2 , b1 =b2

由自然边界条件: -641+2b1=0,62+2b2=0 解方程组,得 41=-u2-1/2,b1=b2=3/2, c1=c2=d1=d2=0. 问题的解 头3 x2, x∈[-1,0] 2 2 S(x)= .3 , x∈[0,1] ●】 8
8 由自然边界条件: 解方程组,得 , [ , ] , [ , ] ( ) 0 1 2 3 2 1 1 0 2 3 2 1 3 2 3 2 x x x x x x S x 问题的解 a1=-a2=1/2, b1=b2=3/2, – 6a1+2b1 =0, 6a2+2b2 =0 c1=c2=d1=d2=0

三次Hermite插值 H(x)=yoao(x)+ya(x)+mBo(x)+mB(x) a)=(1+2二二PR(x)=(x-x)(-)2 X1-X0X1-X0 X1-X0 a()=1+2二二花A(e)=(c-x二 X1-X0 x1-X0 1-X0 x Xo X1 x Xo x1 a(x) 1 0 B(x) 0 0 ai(x) 0 0 B6(x) 1 0 a,(x) 0 1 B(x) 0 0 af(x) 0 0 β1(x) 0 1 9
9 ( ) ( ) ( ) ( ) ( ) 0 0 1 1 0 0 1 1 H x y x y x m x m x 2 1 0 1 1 0 0 0 ( ) (1 2 )( ) x x x x x x x x x 2 1 0 0 1 0 1 1 ( ) (1 2 )( ) x x x x x x x x x 2 1 0 1 0 0 ( ) ( )( ) x x x x x x x 2 1 0 0 1 1 ( ) ( )( ) x x x x x x x x0 x1 1 0 0 0 0 1 0 0 ( ) 0 x ( ) 1 x ( ) 0 x ( ) 1 x x ( ) 1 x ( ) 0 x x0 x1 0 0 1 0 0 0 1 (x) 0 1 ( ) 0 x x 三次Hermite插值

用一阶导数表示的样条 已知函数表 X Xo x1 ●·●●●● Xn fx) Yo V ●●●●●● Yn 设f)在各插值节点x处的一阶导数为m 取1-=h,(j=0,1,2,,n).当x∈+时, 分段Hermite插值 s=42角之6i+0- +代-xXm+6x-xX房ymn 10
10 用一阶导数表示的样条 已知函数表 x x0 x1 ······ xn f(x) y0 y1 ······ yn 设 f(x) 在各插值节点 xj 处的一阶导数为 mj 取 xj+1 – xj = h,( j = 0,1,2,···,n). 当 x∈[xj, xj+ 1]时, 分段Hermite插值 1 2 1 1 2 1 1 2 1 2 1 2 1 2 j j j j j j j j j j j j m h x x m x x h x x x x y h x x h x x y h x x h x x S x ( )( ) ( )( ) ( ) ( )( ) ( )( )