电子科技大学：《数值分析 Numerical Analysis》课程教学资源（课件讲稿）数据拟合

数据拟合 数据拟合的基本概念 数据拟合的线性模型 数据拟合的非线性模型

1 数据拟合的基本概念 数据拟合的线性模型 数据拟合的非线性模型 数据拟合

拟合问题引例1 已知热敏电阻数据： 温度C) 20.532.751.073.095.7 电阻R(2)765 826873 9421032 求60C时的电阻R。 1100 + 1000 设R=at+b 900 ,b为待定系数 + 800 70 20 40 60 80 100 2

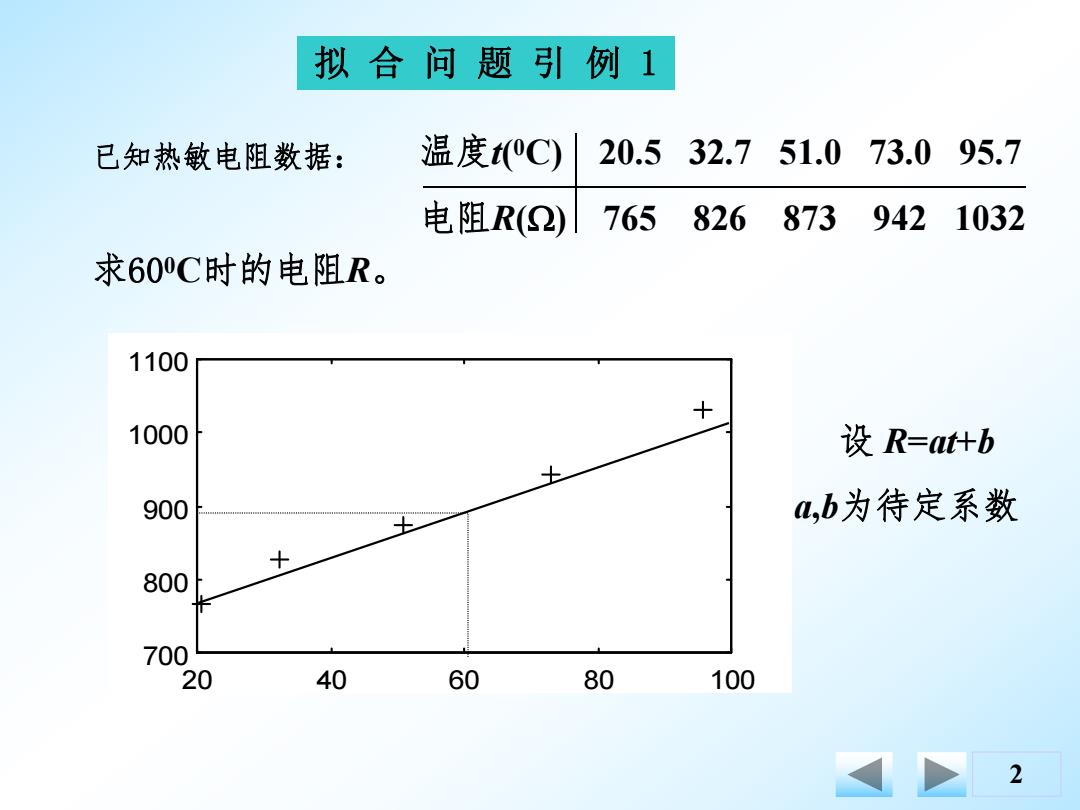
2 拟 合 问 题 引 例 1 温度t( 0C) 20.5 32.7 51.0 73.0 95.7 电阻R() 765 826 873 942 1032 已知热敏电阻数据： 求60 0C时的电阻R。 20 40 60 80 100 700 800 900 1000 1100 设 R=at+b a,b为待定系数

曲线拟合问题的提法 已知一组（二维)数据，即平面上n个点(x,y)i=1,.n, 寻求一个函数（曲线)y=x),使)在某种准则下与所 有数据点最为接近，即曲线拟合得最好。 yt +=Ar) 6为点(xy)与曲线y=f)的距离 3

3 曲 线 拟 合 问 题 的 提 法 已知一组（二维）数据，即平面上 n个点（xi,yi) i=1,…n, 寻求一个函数（曲线）y = f(x), 使 f(x) 在某种准则下与所 有数据点最为接近，即曲线拟合得最好。 + + + + + + + + + x y y = f(x) (xi,yi) i i为点（xi,yi) 与曲线 y = f(x) 的距离

拟合与插值的关系 问题：给定一批数据点，需确定满足特定要求的曲线或曲面 解决方案： 若要求所求曲线（面）通过所给所有数据点，就是插值问题； 若不要求曲线（面）通过所有数据点，而是要求它反映对 象整体的变化趋势，这就是数据拟合，又称曲线拟合或曲 面拟合。 函数插值与曲线拟合都是要根据一组数据构造一个函数 作为近似，由于近似的要求不同，二者的数学方法上是完全 不同的

4 拟合与插值的关系 函数插值与曲线拟合都是要根据一组数据构造一个函数 作为近似，由于近似的要求不同，二者的数学方法上是完全 不同的。 问题：给定一批数据点，需确定满足特定要求的曲线或曲面 解决方案： •若不要求曲线（面）通过所有数据点，而是要求它反映对 象整体的变化趋势，这就是数据拟合，又称曲线拟合或曲 面拟合。 •若要求所求曲线（面）通过所给所有数据点，就是插值问题;

最临近插值、线性插值、样条插值与曲线拟合结果： 25 25 0 20 15 15 10 已知数据点 10 已知数据点 5 nearest linest 曲线拟合 5 曲线拟合 0 0 0 5 10 15 20 0 5 10 15 20 25 20 80 15 10 已知数据点 5 spline 曲线拟合 0 5 10 15 20 5

5 最临近插值、线性插值、样条插值与曲线拟合结果：

离散数据的线性拟合 已知数据表 X X1 x2 Xm fx) y1y'2 Vm 求拟合函数：p(x)=M+bx a+bx=y a+bx2=y2 1 y 1 …: … 》 GX-F a+bxm=ym 1 Xm ym」 超定方程组 6

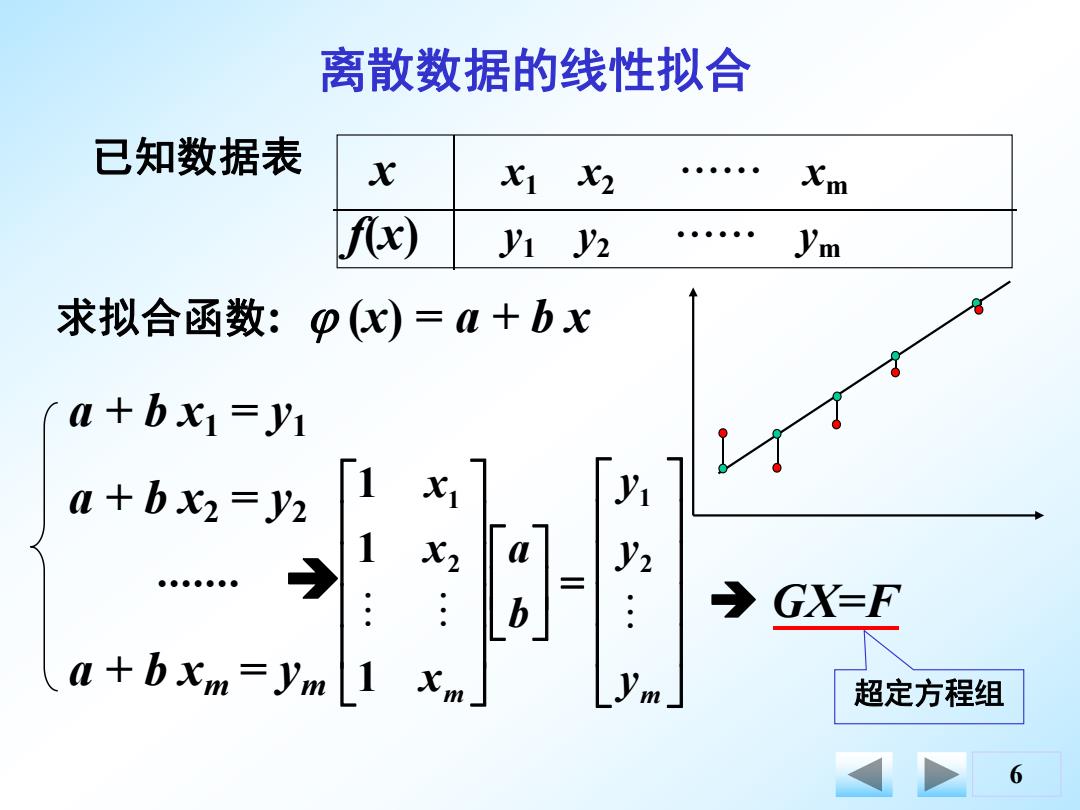
6 已知数据表 x x1 x2 ······ xm f(x) y1 y2 ······ ym 离散数据的线性拟合 求拟合函数:  (x) = a + b x a + b x1 = y1 a + b x2 = y2 ······· a + b xm = ym                    m m y y y b a x x x    2 1 2 1 1 1 1  GX=F 超定方程组

残差：r=GX-F 最小二乘问题 min GX-F2 X∈R2 GX-F=GX-F,GX-F) (GX,GX)-2(GX,F)+F,F) G7GX)-2,GTF)+(F,F) )=(X,GTGX)-2(X,GTF) 求解极值问题： min f(X)=min[(X,G'GX)-2(X,GF)] X∈R2 X∈R2 7

7 2 2 min ||GX F || X R   最小二乘问题 残差: r = GX – F = (GX–F , GX–F ) =(GX, GX) – 2(GX, F )+(F, F) =(X, GTGX) – 2(X, GTF )+(F, F) f(X) = (X, GTGX) – 2(X, GTF ) 求解极值问题: min ( ) min[( , ) 2( , )] 2 2 f X X G GX X G F T T X R X R     2 2 ||GX  F ||

设X*是函数f)的极值点，任意e∈R2 f(X*+te)=(X*+te,GTG(X*+te))-2(X*+te,GTF) g(t)=fX*+te)=fX)+2t(e,GT(GX*-F))+P(e,GTGe) g'(0)=0今(e,G7(GX*-F)=0今 e,GTGX*-F)=0GTGX*F=0 GTGX*GTF-0 GTGX*GTF 令A=GTG,B=GTF→AX*=B对称正定方程组 8

8 g(t)=f(X*+ te) = f(X*)+2t(e, GT(GX*–F))+ t2(e, GTGe) g’(0)=0  (e, GT(GX *– F))=0  (e, GT(GX* – F)) = 0  GT(GX*– F) = 0 GTGX*– GTF = 0  GTGX*=GTF 设 X* 是函数 f(X) 的极值点,任意 e∈R2 f (X*+ te)=(X*+ te, GTG(X*+te)) – 2(X*+te, GTF ) 令 A = GTG, B = GTF  AX* =B

超定方程组最小二乘解X*的几何意义 2x+4y=11 「2 4 例 3x-5y=3 11 G= 3 -5 B= x+2y=6 1 25 6 1lB-GXmigllB-GX ll. 向量组 G=[a1,2] 正规方程GTGX=GrB 平面π GX=xa+ya2 GB-GX=0 Grmin =0 Tmin =B-GX (GX",rmin)=0 GX" π 9

9            2 6 3 5 3 2 4 11 x y x y x y 超定方程组最小二乘解 X*的几何意义        6 3 11  2 2 * || GX || min || GX || X R               1 2 3 5 2 4 例 G [ , ] 向量组 G  1  2 1  2 平面 GX  x  y   * GX * rmin    GX ( , min ) 0 * GX r   T T G GX  G 正规方程 * ( ) 0 * G  GX  T  G rmin  0 T

S(a,b)=‖rl3=∑I(a+bxk)-y]2 k=1 求，b使S(a,b)=min 超定方程组：GX=F→ 正规方程组：GTGX=GTF 1 1 co- m 1 1 七2 三 Xm」 1 Xm」 10

10      m k k k S a b r a bx y 1 2 2 2 ( , ) || || [( ) ] 求 a, b 使 S(a, b)= min 超定方程组: GX=F  正规方程组: GTGX=GTF                          m j j m j j m j j m m T x x m x x x x x x x G G 1 2 1 2 1 1 1 2 1 1 1 1 1 1    