电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第三章 分离变量法（2/4）

数理方程与特殊函激 第三章分离变量法（二） 主讲：杨春

第三章 分离变量法(二) 主讲：杨春

主要内容 一、拉普拉斯方程定解问题分离变量求解 二、高维混合问题分离变量求解

主要内容 一、拉普拉斯方程定解问题分离变量求解 二、高维混合问题分离变量求解

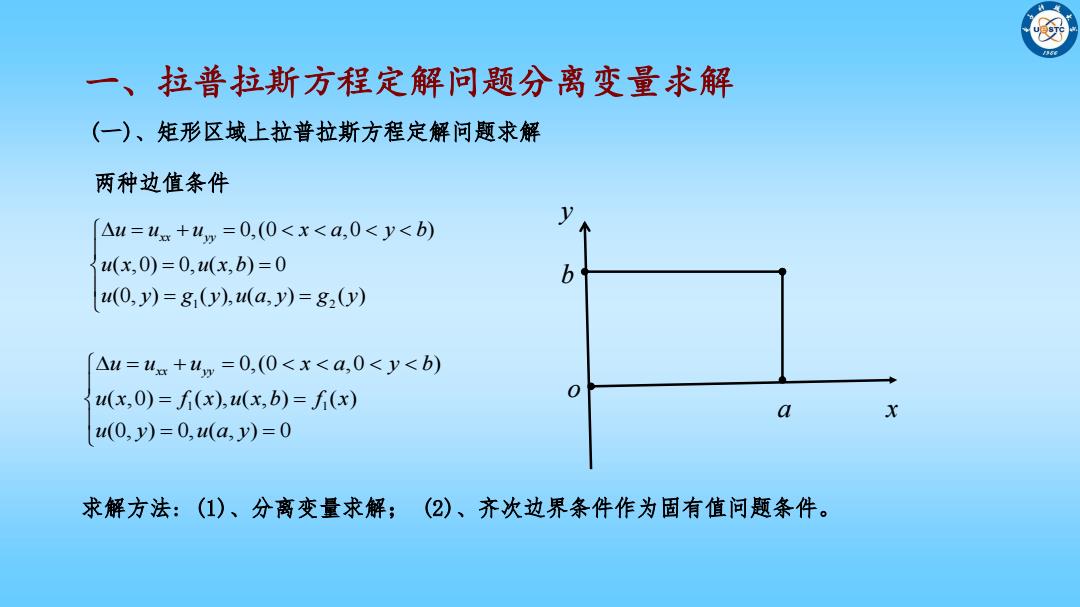
一、拉普拉斯方程定解问题分离变量求解 (一)、矩形区域上拉普拉斯方程定解问题求解 两种边值条件 △u=4.x+4p=0,(0<x<a,0<y<b) u(x,0)=0,u(x,b)=0 b u(0,y)=g(y),(a,y)=g2(y） △u=ux+4w=0,(0<x<a,0<y<b) u(x,0)=f(x),u(x,b)=f(x) 0 a X u(0,y)=0,(a,y)=0 求解方法：(1)、分离变量求解；(2)、齐次边界条件作为固有值问题条件

(一)、矩形区域上拉普拉斯方程定解问题求解 两种边值条件 一、拉普拉斯方程定解问题分离变量求解 1 2 0,(0 ,0 ) ( ,0) 0, ( , ) 0 (0, ) ( ), ( , ) ( ) u u u x a y b xx yy u x u x b u y g y u a y g y                 1 1 0,(0 ,0 ) ( ,0) ( ), ( , ) ( ) (0, ) 0, ( , ) 0 u u u x a y b xx yy u x f x u x b f x u y u a y                 x y a b o 求解方法: (1)、分离变量求解； (2)、齐次边界条件作为固有值问题条件

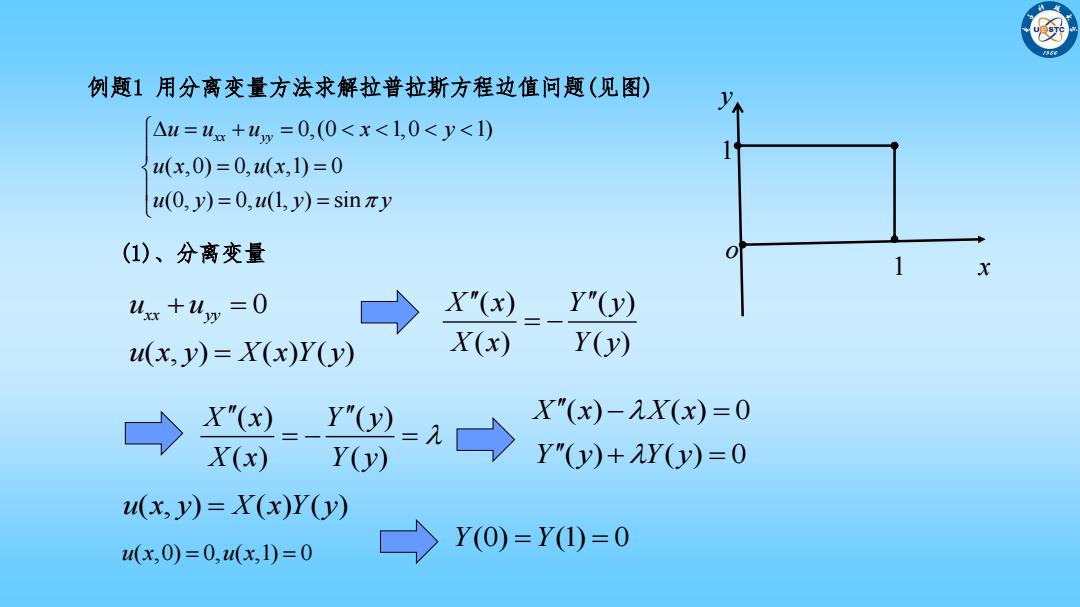
例题1用分离变量方法求解拉普拉斯方程边值问题（见图） △u=4.+4p=0,(0 X"(x)-X(x)=0 X(x) Y(y) Y"(y)+Y(y)=0 u(x,y)=X(x)Y(y) (x,0)=0,(x,1)=0 Y(0)=Y(I)=0

例题1 用分离变量方法求解拉普拉斯方程边值问题(见图) x y 1 1 (1)、分离变量 o 0,(0 1,0 1) ( ,0) 0, ( ,1) 0 (0, ) 0, (1, ) sin u u u x y xx yy u x u x u y u y y                  u u xx yy   0 u x y X x Y y ( , ) ( ) ( )  ( ) ( ) ( ) ( ) X x Y y X x Y y     ( ) ( ) ( ) ( ) X x Y y X x Y y       X x X x ( ) ( ) 0    Y y Y y ( ) ( ) 0    u x y X x Y y ( , ) ( ) ( )  u x u x ( ,0) 0, ( ,1) 0   Y Y (0) (1) 0  

Y"y)+Y(y)=0 于是得到定解问题的固有值问题 Y(0)=Y(I)=0 (2)、求解固有值问题 Y"(y)+Y(y)=0 入n=(nm)2 n=1,2,3,… Y(0)=Y(1①)=0 〉 Y(y)=sinnay (3)、求解另-个常徽分方程X"(x)-1X(x)=0· X"(x)-4X(x)=0 X,(x)=C,e"+D.e-ms X(x)=Cemx +De-nzx Y (y)=sinnay →4，(x,y)=X,x)Y,y)=(C,eax+D,)sinnzy n=1,2,3,…

(2)、求解固有值问题 2 ( )   n  n n 1,2,3, ( ) ( ) 0 (0) (1) 0 Y y Y y Y Y          于是得到定解问题的固有值问题 ( ) ( ) 0 (0) (1) 0 Y y Y y Y Y          Y y n y n ( ) sin   (3)、求解另一个常微分方程 X x X x ( ) ( ) 0    . X x X x ( ) ( ) 0 n    ( ) n x n x X x C e D e n n n      ( ) n x n x X x C e D e n n n      Y y n y n ( ) sin   ( , ) ( ) ( ) sin   n x n x u x y X x Y y C e D e n y n n n n n        n 1,2,3

x.u(.)(C.+De)sinnzy (④)、求定解 xW-2C,e+D,er）sinnry u(0,y)=0 →2(C,+Dj小smny=0→C,+D=0 (CD)sinmy uL,y)=sinπy →iCe+De")iny=sny 只有n=1时，等式才成立！ (Ce+De)sinzy=sinmy Ce+De=1

(4)、求定解   1 1 ( , ) ( , ) sin n x n x n n n n n u x y u x y C e D e n y                1 ( , ) sin n x n x n n n u x y C e D e n y          u y (0, ) 0    1 sin 0 n n n C D n y       0 C D n n     1 ( , ) sin n x n x n n n u x y C e D e n y          u y y (1, ) sin     1 sin sin n n n n n C e D e n y y           只有n=1时，等式才成立！ C e D e y y 1 1 sin sin        1 1 C e D e 1    

C+D=0 Ce+De*=1 D2-e2-1 所以，拉普拉斯方程在该矩形域内的定解为： x0=二e-e"sny 注：教材上采用了双曲函数表示

1 1 C D  0 ( , ) sin 2   1 e x x u x y e e y e          所以，拉普拉斯方程在该矩形域内的定解为： 1 1 C e D e 1     1 2 1 e C e     1 2 1 e D e      注：教材上采用了双曲函数表示

(二)、园域上拉普拉斯方程定解问题求解 1、物理背景与定解问题 一个半径为r。的薄圆盘，上下两面绝热，圆周边缘温度分布为已知，求达到稳 恒状态时圆盘内的温度分布。 分析：(1)这是一个稳态问题，所以温度分布满足拉普拉斯方程： Ou u △，u= 2 =0,(x2+y2<62) 可设边界条件为： x2+=2=f(x,y) 引进极坐标变换： x=rcos 。,(0≤r<+o0,0≤0≤2π) y=rsine

(二)、园域上拉普拉斯方程定解问题求解 1、物理背景与定解问题 一个半径为r0 的薄圆盘，上下两面绝热，圆周边缘温度分布为已知，求达到稳 恒状态时圆盘内的温度分布。 分析:(1)这是一个稳态问题，所以温度分布满足拉普拉斯方程： 2 2 2 2 2 2 0 2 2 0,( ) u u u x y r x y           可设边界条件为： 2 2 2 0 ( , ) x y r u f x y    引进极坐标变换： cos ,(0 ,0 2 ) sin x r r y r              

x=rcos0 (0≤r<+0,0≤0≤2π) y=rsine △2u= 24+0-=0,(2+y2<0) 1 → 14=0.() ou* .r2a02 4,=n=f(0)…(2) 42y6=fx, 2)圆盘中心温度有限，于是有：u(0,O)川<+o…(3) 3)c,9)与c,0+2)是圆盘上同-一点，于是有：u(r,Θ)=u(T,0+2π)…(4) -(r r or ar )+0=0c<)0 定解问题 u(6,0)=f(0)…(2) u(r,0)=u(r,0+2π)…(3) u(0,0)<+oo…(4)

2 2 2 2 2 2 0 2 2 0,( ) u u u x y r x y           (2) 圆盘中心温度有限，于是有： cos ,(0 ,0 2 ) sin x r r y r               0 2 2 2 1 1 ( ) 0 (1) ( ) (2) r r u u r r r r r u f                  2 2 2 0 ( , ) x y r u f x y    u(0, ) (3)    (3) (r,θ)与(r,θ+2π)是圆盘上同一点，于是有： u r u r ( , ) ( , 2 ) (4)      2 2 2 0 0 1 1 ( ) 0,( ) (1) ( , ) ( ) (2) ( , ) ( , 2 ) (3) (0, ) (4) u u u r r r r r r r u r f u r u r u                                定解问题

2、分离变量求解 1oou、1a2u △u= -(r r oror =0,0<6)(0 (山)分离变量 u(6,0)=f(0)…(2) (,0)=R(r)Φ(0) (r,0)=(,0+2π)…(3) u(0,0)<+o.…(4) Au=00)+1=0 r oror r2 00 〉 RD+ro+片Rm-0→ r2R”+rR'( r2R"+rR' = R R Φ Φ”+Φ=0…(6) r2R"+rR'-R=0…(7) Φ”+Φ=0 固有值问题 1Φ(0+2π)=Φ(0)

2、分离变量求解 (1) 分离变量 u r R r ( , ) ( ) ( )     2 2 2 0 0 1 1 ( ) 0,( ) (1) ( , ) ( ) (2) ( , ) ( , 2 ) (3) (0, ) (4) u u u r r r r r r r u r f u r u r u                                2 2 2 1 1 ( ) 0 u u u r r r r r            2 1 1 R R R 0 r r          2 r R rR R         2 r R rR R           2 0 (6) r R rR R 0 (7)             固有值问题                    2 0