电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第六章 Green函数法 6.2 Dirichlet问题求解（2/2）

§6.2 Dirichlet问题求解 定理1 △M=-f(M),M∈V luls=2(M) 的解的积分表达式为 =∯o(u)2Cas+ca:MM,m, Greeni函数 AG=-δ(M-Mo),M∈V CRR书 准格林函数方法的理论及其在力学中的应用 边界元法广泛用宗解庆各件边晚问盟其拉西是津立可墨的暴本制 个在边界上具有奇丹性的积分方程准格 意8，估作·中国力学学合学木大会 Gs=0 凝聚态物理的 格林函数理论 城号引屈：0发表：2005年 准格林函敖方法在弹性扭转问题中的应用 利阳Poissor方程的基本解构造一个#格林墙数这个国数真是Pg 并通过建立一个玩英化的边界方程来表示 王红，寒调·《病理工大学学报白然学) 表2004 的开。中公

§6.2 Dirichlet问题求解 2 定理1 ( ), ( ) S u f M M V u M           的解的积分表达式为   0 0 0 0 0 ( ; ) ( ) ( ; ) ( ) S V G M M u M M dS G M M f M dM n          0 , S 0 G M M M V G            Green函数

用镜像法求Green函数 q 点电荷电势 u= 4元GIMMo 无穷长导线电势 W= 9-1nm 1 2E元 IMMo 两个函数特点 △G=-6(M-M,),M,M∈V △u=0,r≠0

3 用镜像法求Green函数 两个函数特点 0 4 MM q u  r  0 1 ln 2 MM q u  r     u r 0, 0 点电荷电势 无穷长导线电势      G M M M M V   0 0 ,

1.半空间的Green函数 △G=-6(x-5,y-1,2-5),z>0 G--0 G(M;M)=41+u2= [】 4 3.5 1 3 2.5 =4r(M,Mo) 1.5 1 0.5 2=一 4πrM,M) M

4 1. 半空间的Green函数   0 , , , 0 0 z G x y z z G                  1 0 1 4 ( , ) u  r M M  2 1 1 4 ( , ) u  r M M   0 1 2 0 1 1 1 1 4 ( , ) ( ) ( , ; ) u u r M M r M M G M M            M0 M M1

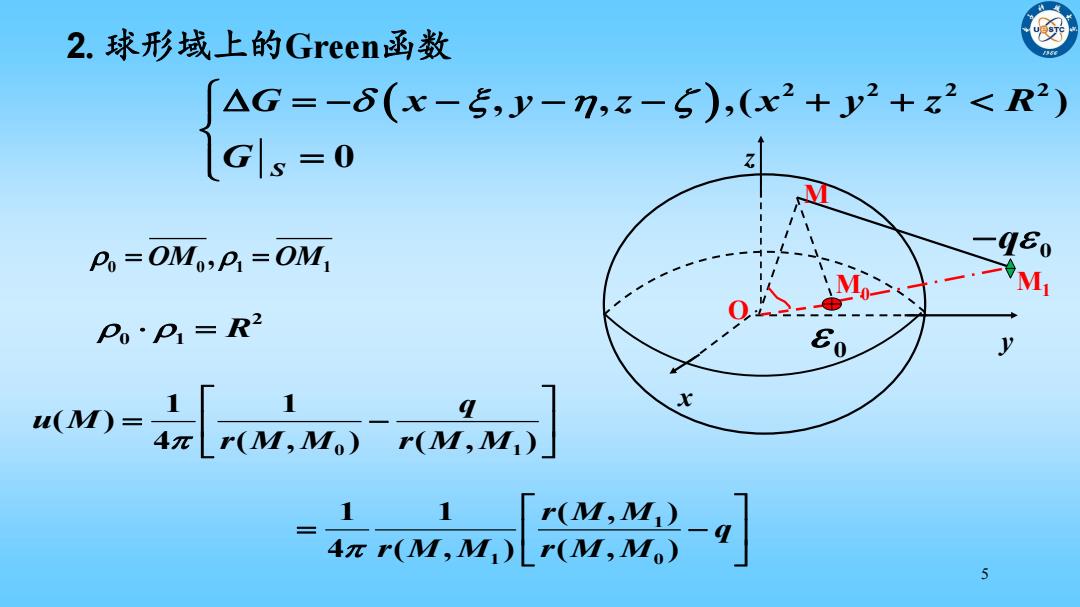
2.球形域上的Green函数 AG=-6(x-5y-7,z-5),(x2+2+z2<R2) lGls-0 Po=OMo,P:=OMT M P0·P1=R2 y uw-[nm] [C}-] 1 5

5 2. 球形域上的Green函数   2 2 2 2 , , ,( ) S 0 G x y z x y z R G                   0 0 1 1     OM OM , 2   0 1   R M z O y x 0  q 0   M0 M1 1 1 0 1 1 ( , ) 4 ( , ) ( , ) r M M q  r M M r M M         0 1 1 1 ( ) 4 ( , ) ( , ) q u M  r M M r M M        

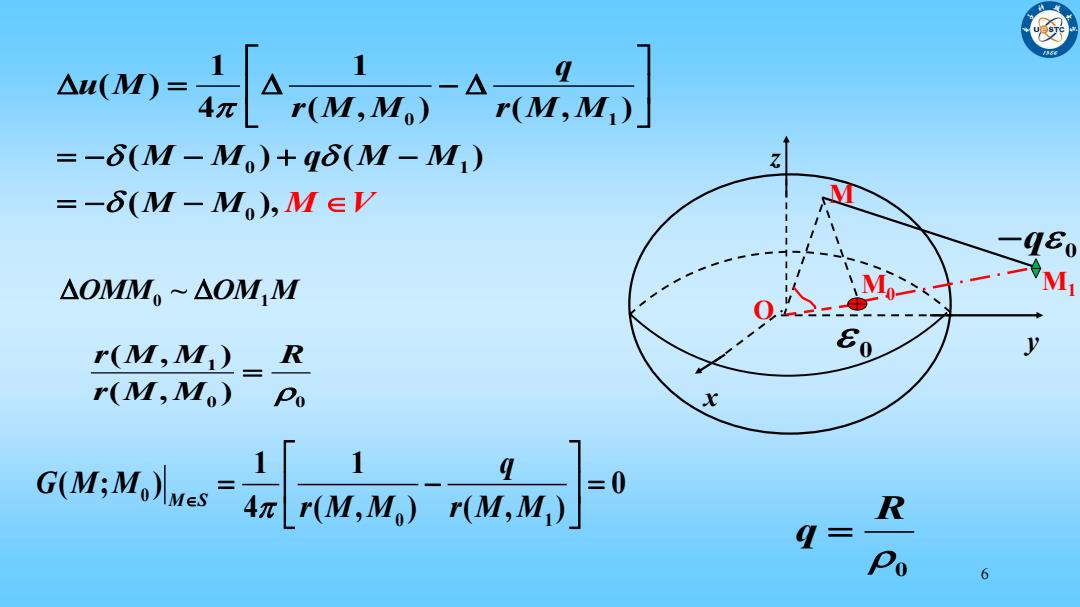
=-6(M-M,)+q6(M-M1) =-6(M-M),M∈V △OMM.~△OMM .9M1 r(M,M) R y r(M,Mo) Po anwl一Lgwi R Po 6

6 0 1 0 1 0 1 1 ( ) 4 ( , ) ( , ) ( ) ( ) ( ), M q u M r M M r M M M M q M M V M M                         1 0 0 ( , ) ( , ) r M M R r M M   0 1   OMM OM M ~ 0 0 1 1 1 0 4 ( , ) ( , ) ( ; ) M S q r M M G M M   r M M          0 R q   M z O y x 0  q 0   M0 M1

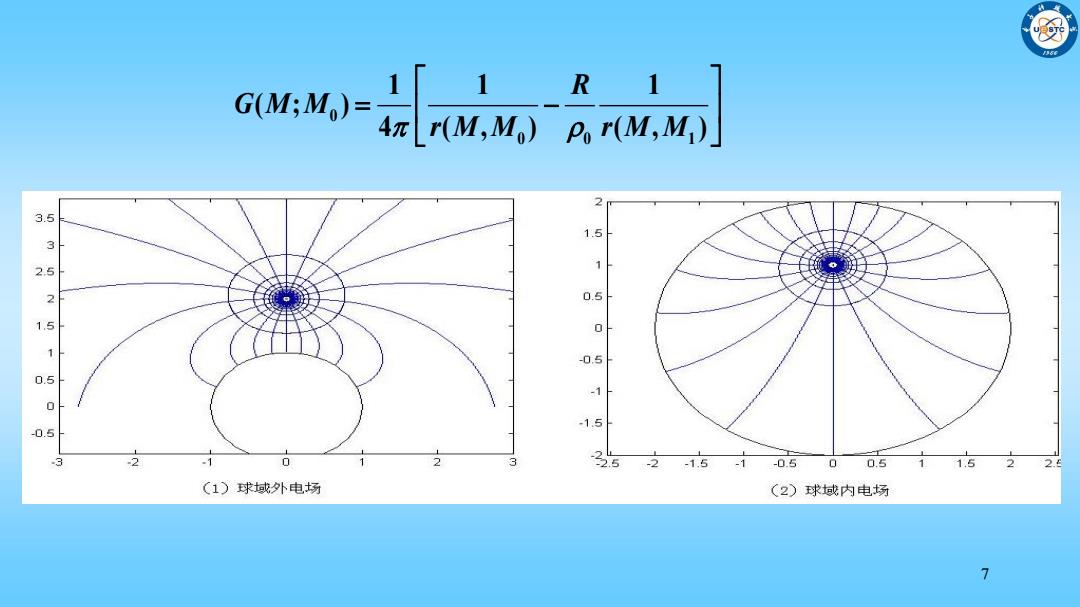
ouw=员 2 3.5 1.5 352 0.5 151 -0.5 -1 -1.5 2 1 0 2 225 1.51 -0.5 0 0.5 1 1.5 2.9 (1)球域外电场 (2)球域内电场 7

7 0 0 0 1 1 1 1 4 ( , ) ( ; ) ( , ) R r M M r G M M   M M        

3.圆域上的Green函数 △G(M;M)=-6(M-Mo),(x2+y2<R2) G2=0 M 1 M In 2π Mo 会 0 R In 2元 9太}

8 3. 圆域上的Green函数 0 2 2 2 0 ( ; ) ( ),( ) 0 L M M x R G       G M M  y     1 0 1 0 1 1 1 1 ln ln ln 2 2 MM MM MM MM r v   r r r            1 0 0 1 1 ln ln 2 2 MM L MM L r R v   r r           0 1 0 0 1 1 1 ln ln l 2 ( ; ) n MM MM G M r M R  r r            0 1 0 1 1 1 ln ln 2 MM MM R  r r r                   L O M0 M1 M

4.上半平面的Green函数 △G=-δ(M-M,),y>0 M 1G-o=0 G(M;M.)- 〔点) M 9

9 4. 上半平面的Green函数 0 1 0 1 1 1 ( ; ) ln ln 2 MM MM G M M  r r           0 0 ( ), 0 y 0 G M M y G            M M1 M0

5.第一象限上的格林函数 △G(M;M)=-6(M-M,),x>0,y>0 G(M;Mo)o=0,G(M;Mo)=0=0 10 8 2 容 ⊕ M3 M2 6 -8 90 -8 -6 1 1 1 In- 2元 1 In 元 IMM2 2元 IMM3 10

10 0 0 0 0 0 0 ( ; ) ( ), 0, 0 ( ; ) 0, ( ; ) 0 x y G M M M M x y G M M G M M               5. 第一象限上的格林函数 1 2 3 1 1 1 1 1 1 ln , ln , ln 2 2 2    r r r MM MM MM  

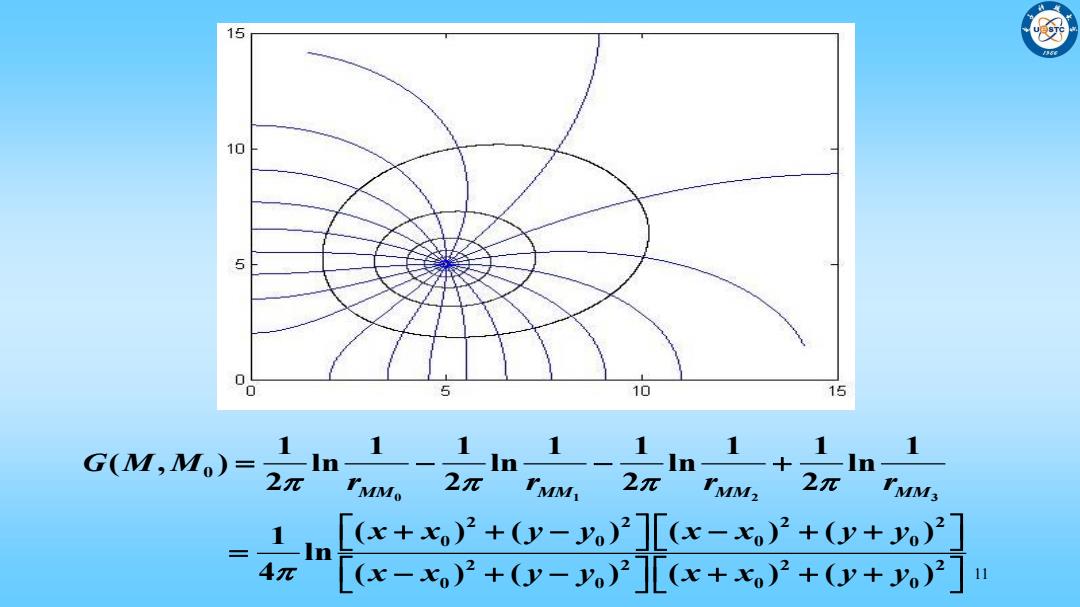
15 10 5 0 0 5 10 15 G(M,Mo)= ,n1-,n L-1n1+n1 2元 MM 2元“ IMM2 2元 IMM3 -8g4 1

11 0 1 2 3 0 2 2 2 2 0 0 0 0 2 2 2 2 0 0 0 0 1 1 1 1 1 1 1 1 ( , ) ln ln ln ln 2 2 2 2 1 ( ) ( ) ( ) ( ) ln 4 ( ) ( ) ( ) ( ) MM MM MM MM G M M r r r r x x y y x x y y x x y y x x y y                                      