
《矩阵理论》 第三章矩阵分解 数学科学学院 2021年9月 4口+4四,,左·生·生Q0 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月1/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 《矩阵理论》 第三章矩阵分解 数学科学学院 2021 年 9 月 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 1 / 61
3.1节:矩阵的三角分解 定义3.1.1 如果a(i=1,2,·,n)均为正实数 a∈C(R)(i<j,i=1,2,…,n-1;j=i+1,i+2,…,n), 口4·2·生·生分QC 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月2/61
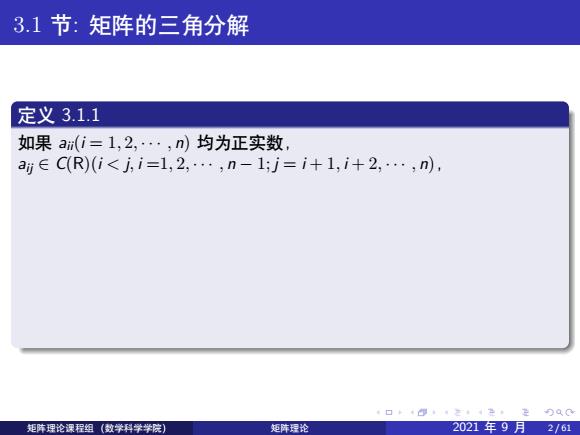
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定义 3.1.1 如果 aii(i = 1, 2, · · · , n) 均为正实数, aij ∈ C(R)(i < j, i =1, 2, · · · , n − 1; j = i + 1, i + 2, · · · , n), 则上三角矩阵 R = a11 a12 · · · a1n 0 a22 · · · a2n . . . . . . . . . . . . 0 0 · · · ann 称为正线上三角复 (实) 矩阵. 特别当 aii = 1(i = 1, 2, · · · , n) 时,R 称为 单位上三角复 (实) 矩阵. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 2 / 61

3.1节:矩阵的三角分解 定义3.1.1 如果a(i=1,2,·,n)均为正实数 a时∈C(R)(i<j,i=1,2,…,n-1;j=i+1,i+2,…,n), 则上三角矩阵 a11 a12 ain 0 a22 a2n R= 0 0 ann 4口+·左·生·生分Q0 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月2/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定义 3.1.1 如果 aii(i = 1, 2, · · · , n) 均为正实数, aij ∈ C(R)(i < j, i =1, 2, · · · , n − 1; j = i + 1, i + 2, · · · , n), 则上三角矩阵 R = a11 a12 · · · a1n 0 a22 · · · a2n . . . . . . . . . . . . 0 0 · · · ann 称为正线上三角复 (实) 矩阵. 特别当 aii = 1(i = 1, 2, · · · , n) 时,R 称为 单位上三角复 (实) 矩阵. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 2 / 61

3.1节:矩阵的三角分解 定义3.1.1 如果a(i=1,2,·,n)均为正实数 a时∈C(R)(i<,i=1,2,…,n-1j=i+1,i+2,…,n), 则上三角矩阵 a11 a12 a1n 0 a22 a2n R= 0 0 ann 称为正线上三角复(实)矩阵.特别当ai=1(i=1,2,·,n)时,R称为 单位上三角复(实)矩阵 口+4①·左·生生Q0 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月2/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定义 3.1.1 如果 aii(i = 1, 2, · · · , n) 均为正实数, aij ∈ C(R)(i < j, i =1, 2, · · · , n − 1; j = i + 1, i + 2, · · · , n), 则上三角矩阵 R = a11 a12 · · · a1n 0 a22 · · · a2n . . . . . . . . . . . . 0 0 · · · ann 称为正线上三角复 (实) 矩阵. 特别当 aii = 1(i = 1, 2, · · · , n) 时,R 称为 单位上三角复 (实) 矩阵. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 2 / 61

3.1节:矩阵的三角分解 定义3.1.2 如果am(i=1,2,…,n)均为正实数,a时∈C(R)(i>jJ= 1,2,·,n-1;i=j+1,j+2,,n, 4口+4四,左·生·生分QC 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月3/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定义 3.1.2 如果 aii(i = 1, 2, · · · , n) 均为正实数,aij ∈ C(R)(i > j, j = 1, 2, · · · , n − 1; i = j + 1, j + 2, · · · , n), 则下三角矩阵 L = a11 0 · · · 0 a21 a22 · · · 0 . . . . . . . . . . . . an1 an2 · · · ann 称为正线下三角复 (实) 矩阵. 特别当 aii = 1(i = 1, 2, · · · , n) 时,R 称为 单位下三角复 (实) 矩阵. 为了方便起见,我们用 C m×n r (R m×n r ) 表示复数 (实数) 域上秩为 r 的 m × n 矩阵的集合. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 3 / 61

3.1节:矩阵的三角分解 定义31.2 如果ami=1,2,·,n)均为正实数,a时∈C(R)(i>j,j= 1,2,…,n-1;i=j+1,j+2,…,n, 则下三角矩阵 a11 0 0 a21 a22 0 L= ·.. anl an2 ann 口4·2·生·生分QC 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月3/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定义 3.1.2 如果 aii(i = 1, 2, · · · , n) 均为正实数,aij ∈ C(R)(i > j, j = 1, 2, · · · , n − 1; i = j + 1, j + 2, · · · , n), 则下三角矩阵 L = a11 0 · · · 0 a21 a22 · · · 0 . . . . . . . . . . . . an1 an2 · · · ann 称为正线下三角复 (实) 矩阵. 特别当 aii = 1(i = 1, 2, · · · , n) 时,R 称为 单位下三角复 (实) 矩阵. 为了方便起见,我们用 C m×n r (R m×n r ) 表示复数 (实数) 域上秩为 r 的 m × n 矩阵的集合. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 3 / 61

3.1节:矩阵的三角分解 定义3.1.2 如果am(i=1,2,…,n)均为正实数,a∈C(R)(i>jJ= 1,2,…,n-1;i=j+1,j+2,…,n, 则下三角矩阵 a11 0 0 a21 a22 0 L= anl an2 ann/ 称为正线下三角复(实)矩阵.特别当a=1(i=1,2,·,n)时,R称为 单位下三角复(实)矩阵 为了方便起见,我们用C”x”(R四x)表示复数(实数)域上秩为r的 m×n矩阵的集合 是月a0 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月3/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定义 3.1.2 如果 aii(i = 1, 2, · · · , n) 均为正实数,aij ∈ C(R)(i > j, j = 1, 2, · · · , n − 1; i = j + 1, j + 2, · · · , n), 则下三角矩阵 L = a11 0 · · · 0 a21 a22 · · · 0 . . . . . . . . . . . . an1 an2 · · · ann 称为正线下三角复 (实) 矩阵. 特别当 aii = 1(i = 1, 2, · · · , n) 时,R 称为 单位下三角复 (实) 矩阵. 为了方便起见,我们用 C m×n r (R m×n r ) 表示复数 (实数) 域上秩为 r 的 m × n 矩阵的集合. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 3 / 61

3.1节:矩阵的三角分解 定理3.1.1 设A∈C?xn,则A可以唯一地分解为 A=U1R,(3.1.1) 其中U1是n阶酉矩阵,R为n阶正线上三角复矩阵; 4口+4四,,左·生·生Q0 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月4/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定理 3.1.1 设 A ∈ C n×n n ,则 A 可以唯一地分解为 A = U1R,(3.1.1) 其中 U1 是 n 阶酉矩阵,R 为 n 阶正线上三角复矩阵; 或 A 可以唯一地分解为 A = LU2,(3.1.2) 其中 U2 是 n 阶酉矩阵,L 为 n 阶正线下三角复矩阵. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 4 / 61

3.1节:矩阵的三角分解 定理3.1.1 设A∈C?xn,则A可以唯一地分解为 A=U1R,(3.1.1) 其中U1是n阶酉矩阵,R为n阶正线上三角复矩阵; 或A可以唯一地分解为 A=L2,(3.1.2) 其中U2是n阶酉矩阵,L为n阶正线下三角复矩阵 口4·2·生·生分QC 矩阵理论课程组(数学科学学院)】 矩阵理论 2021年9月4/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 定理 3.1.1 设 A ∈ C n×n n ,则 A 可以唯一地分解为 A = U1R,(3.1.1) 其中 U1 是 n 阶酉矩阵,R 为 n 阶正线上三角复矩阵; 或 A 可以唯一地分解为 A = LU2,(3.1.2) 其中 U2 是 n 阶酉矩阵,L 为 n 阶正线下三角复矩阵. 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 4 / 61

3.1节:矩阵的三角分解 证:把矩阵A按列分块可得A=(a1,a2,·,an).由于A的秩为n,故 a1,Q2,…,an线性无关.将a1,a2,·,an斯密特正交化、单位化得 6= 01 a12, -1 B:= -昌a.g i=2,3…·,n. (1) (a,8)3 口+4①,,之·生生分Q0 矩阵理论课程组(数学科学学院) 矩阵理论 2021年9月5/61
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.1 节: 矩阵的三角分解 证: 把矩阵 A 按列分块可得 A = (α1, α2, · · · , αn). 由于 A 的秩为 n,故 α1, α2, · · · , αn 线性无关. 将 α1, α2, · · · , αn 斯密特正交化、单位化得 β1 = α1 ||α1||2 , βi = αi− i∑−1 j=1 (αi ,βj)βj αi− i∑−1 j=1 (αi ,βj)βj , i = 2, 3, · · · , n. (1) 令 矩阵理论课程组 (数学科学学院) 矩阵理论 2021 年 9 月 5 / 61