
1 数论基础
数论基础 1

回顾 2 问题1:什么是集合的基数? 有限集合的基数就是一个自然数,表示集合的元素个数 无限集合中最小的那一个就是自然数集合,它的基数是X。 我们也可以判断一个集合是有限还是无限 问题2:(基数)最大的集合有多大? 实数集比自然数集大 任意集合的幂集比自身大 问题3:如何比较两个(无限)集合的基数? 利用双射函数证明等势 利用Bernstein定理证明等势
回顾 2 问题1:什么是集合的基数? - 有限集合的基数就是一个自然数,表示集合的元素个数 - 无限集合中最小的那一个就是自然数集合,它的基数是ℵ0 - 我们也可以判断一个集合是有限还是无限 问题2:(基数)最大的集合有多大? - 实数集比自然数集大 - 任意集合的幂集比自身大 问题3:如何比较两个(无限)集合的基数? - 利用双射函数证明等势 - 利用Bernstein定理证明等势

本节提要 3 问题1:什么是(初等)数论? 问题2:素数有哪些性质?
本节提要 3 问题1:什么是(初等)数论? 问题2:素数有哪些性质?

现代数论的早期铺垫 4 证明质数无穷 -Euclid:Elements (~300 A.D.) 筛法寻找质数 Eratosthenes (~250 A.D.) 辗转相除法求最大公约数 N-I Euclid:Elements (~300 A.D.) ■求解同余方程的中国剩余定理 《孙子算经》(~420B.C.)
现代数论的早期铺垫 4

什么是数论 5 数论是纯数学的一个分支,也是纯数学的代 表,它主要研究整数的性质 ■数论的早期研究可追溯至Euclid时期(~300 B.C.):对质数和整除的研究 中国古代(~400A.D.)对同余方程的研究 为现代数论作出了基础性贡献
什么是数论 5

整数集 6 整数集一般记为Z(来源于德语“数”: Zahlen的首字母),同时用Z+表示正整数集 (N-{0}),用Z-表示负整数集(Z-N) Z为可列集:Z≈N,基数为Xg Z是全序集味来课程详述),无上界和下界 Z和加法运算形成一个循环群(未来课程详述);和 加法运算及乘法运算形成一个环(参见抽象代数资料*)
整数集 6
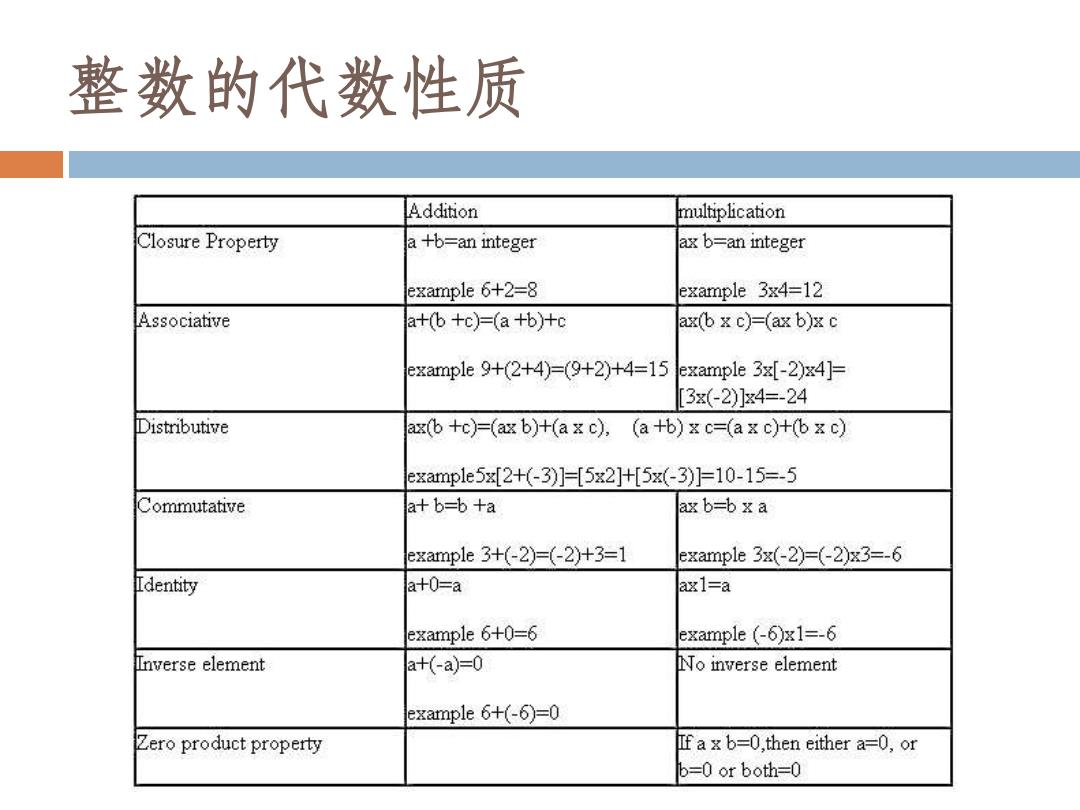
整数的代数性质 Addition multiplication Closure Property a +b=an integer ax b=an integer example 6+2=8 example 3x4=12 Associative a+(b+c)=(a+b)+c ax(b x c)=(ax b)x c example9+(2+4)=(9+2)+4=15 example3z[-2)x4]= 3x(-2)]x4=-24 Distributive ax(b+c)=(ax b)+(a xc),(a+b)xc=(a xc)+(bxc) example5x[2+(-3)]=[5x2]H[5x(-3)]=10-15=-5 Commutative a+b-b +a ax b=b x a example3+(-2)=(-2)+3=1 example3x(-2)=(-2)x3=-6 Identity a+0=a ax1=a example 6+0=6 example (-6)x1=-6 Inverse element a+(-a)=0 No inverse element example 6+(-6)=0 Zero product property If a x b=0,then either a=0,or b=0 or both=0
整数的代数性质

整除 口对任意整数a和b,a≠0,我们说a整除b(记作叫b), 如果存在整数c使得b=ac. 口设,b和c是整数,M≠0, 口若db,且ac,则a(b+c) ▣若db,则bc) o若ab,且blc,则dlc
整除 对任意整数a和b, a 0, 我们说a整除b (记作a|b) , 如果存在整数c使得b = a c . 设a, b和c是整数,a 0, 若a|b,且 a|c,则 a|(b+c) 若a|b,则 a|(b c) 若a|b,且 b|c,则 a|c

余数 余数(remainder)来源于带余除法 定义(带余除法):令a∈Z,d∈Z+,则: (3!q,r∈Z∧0≤r<d)(a=d×q+r) 0 其中,a称为被除数(dividend),d称为除数 (divisor),q称为商(quotient),r称为余数 0 记:q=adiv d,r=a mod d,后者读作“a模b” 例:-11=3×(-4)+1,·-11m0d3=1
余数

同余算术(高斯,Gauss) 设a和b为整数,m为正整数,如果m整除(b-a),就 说a模m同余b.记作a三b(modm). ●a三b(modm)iffa(modm)=b(modm) ●a三b(modm)iff3k∈Z.a=b+km ● 举例-1≡5(m0d6),-2=4(m0d6),,-5≡1(m0d6) ●[0]={.,-6,0,6,…} 。[1]={..-5,1,7,…} ●[2]={.,-4,2,8,…}
同余算术 (高斯, Gauss)