
1 二部图与匹配
二部图与匹配 1

上节回顾 ▣内容1:Dijkstra算法 口内容2:Floyd-Warshall算法 ▣内容3:旅行商问题(TSP) ▣内容4:最大流问题
内容1:Dijkstra算法 内容2:Floyd-Warshall算法 内容3:旅行商问题(TSP) 内容4:最大流问题* 上节回顾

本节提要 口问题1:什么是二部图及其匹配? 口问题2:二部图中的有哪些匹配?
问题1:什么是二部图及其匹配? 问题2:二部图中的有哪些匹配? 本节提要
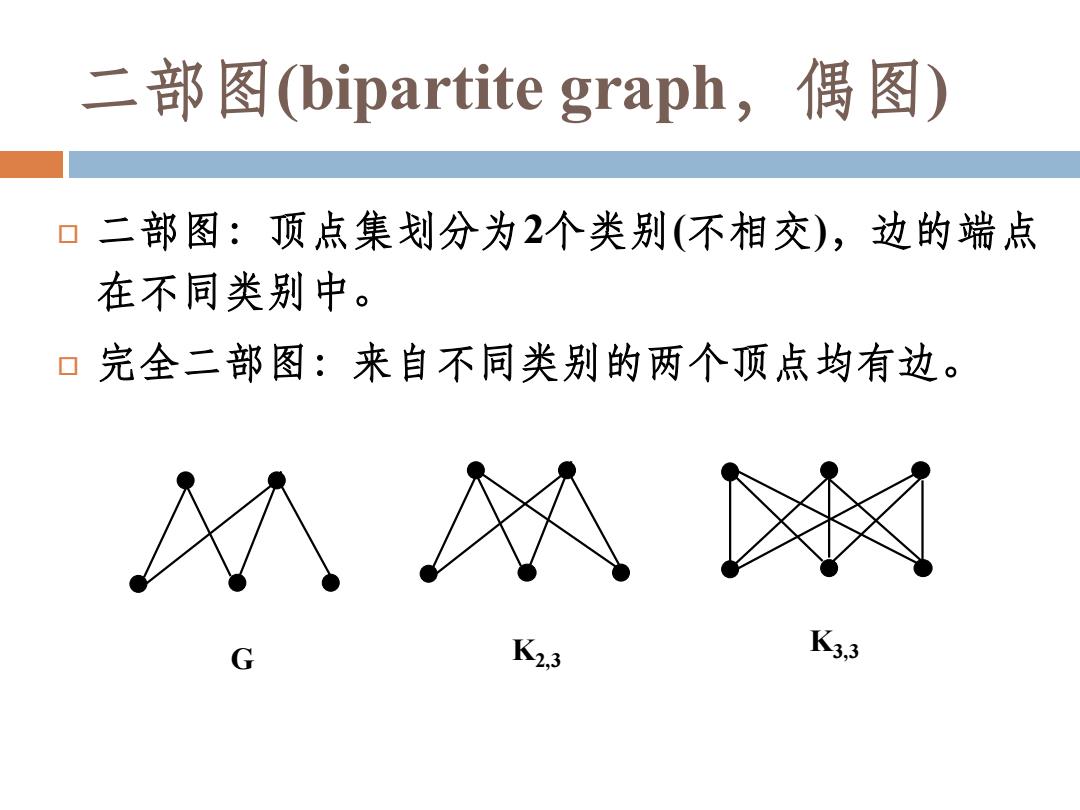
二部图(bipartite graph,偶图) 二部图:顶点集划分为2个类别(不相交),边的端点 在不同类别中。 口完全二部图:来自不同类别的两个顶点均有边。 G K23 K33
二部图(bipartite graph,偶图) 二部图:顶点集划分为2个类别(不相交),边的端点 在不同类别中。 完全二部图:来自不同类别的两个顶点均有边。 K2,3 G K3,3
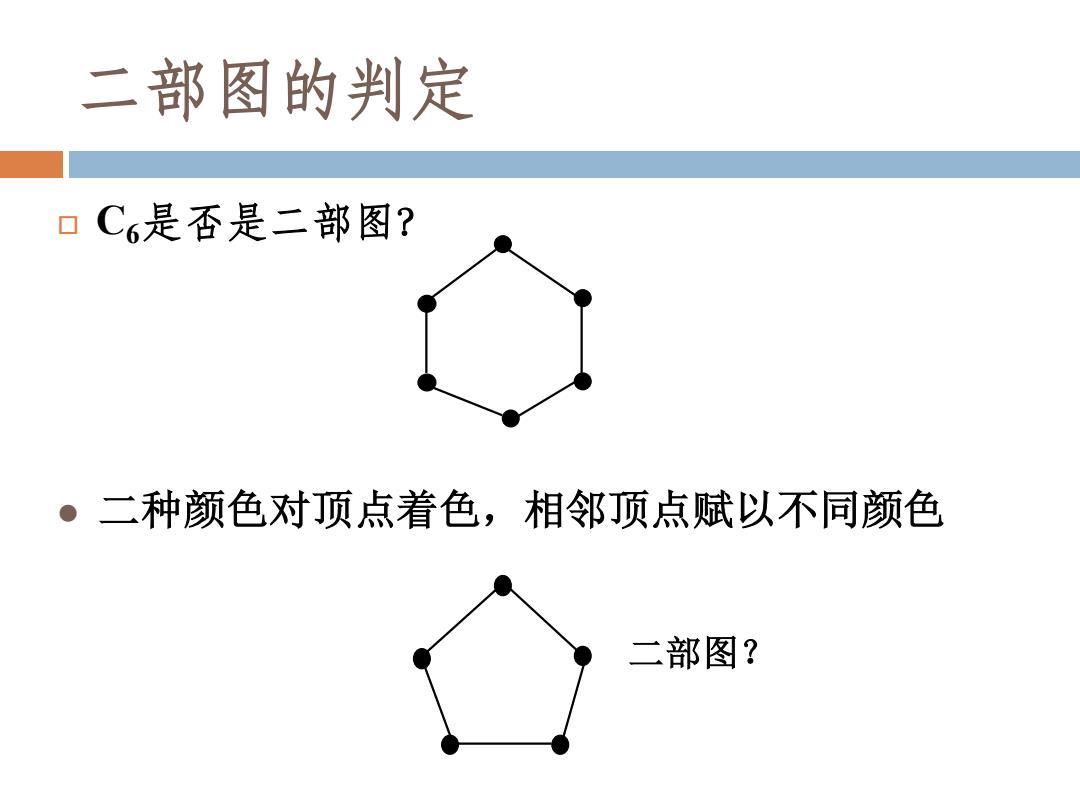
二部图的判定 口C6是否是二部图? ·二种颜色对顶点着色,相邻顶点赋以不同颜色 二部图?
二部图的判定 C6是否是二部图? ⚫ 二种颜色对顶点着色,相邻顶点赋以不同颜色 二部图?
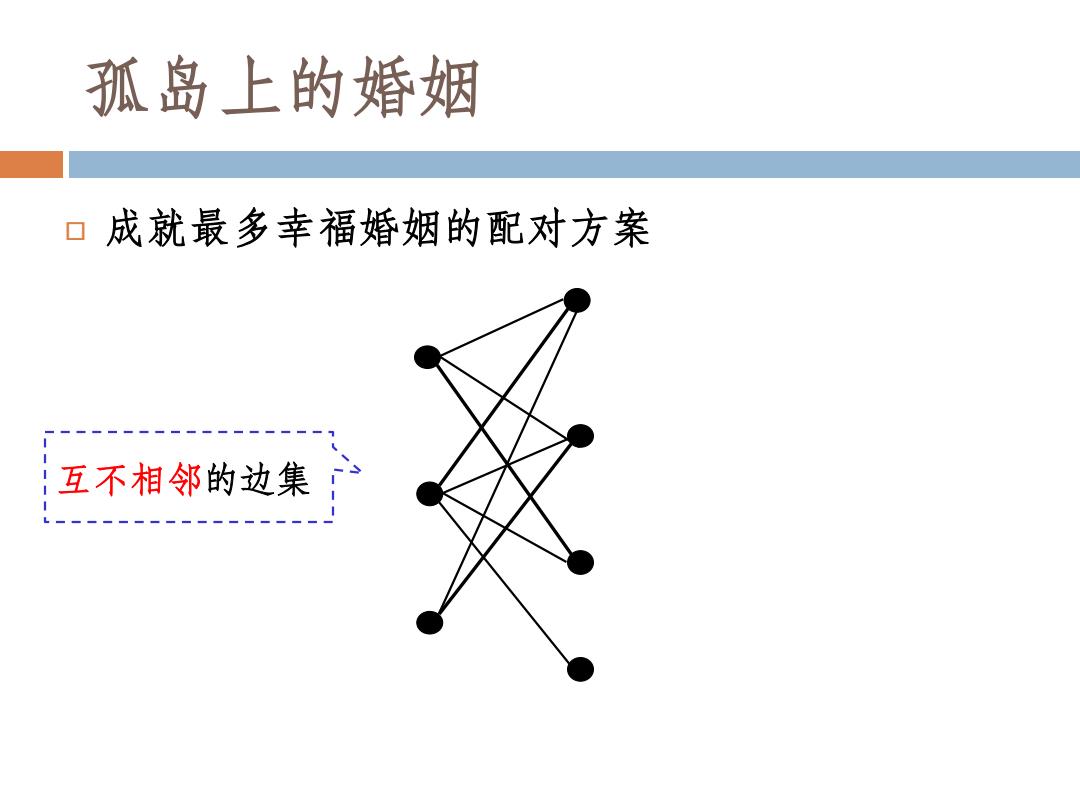
孤岛上的婚姻 口成就最多幸福婚姻的配对方案 互不相邻的边集
成就最多幸福婚姻的配对方案 互不相邻的边集 孤岛上的婚姻
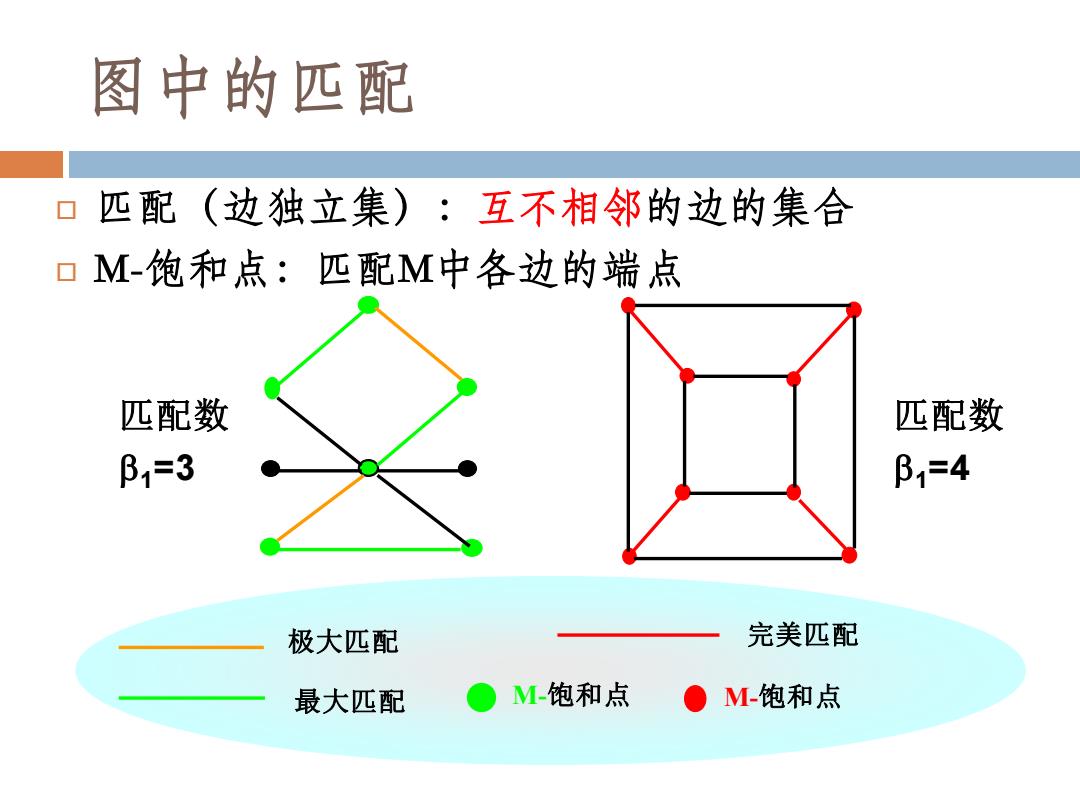
图中的匹配 匹配(边独立集):互不相邻的边的集合 口M-饱和点:匹配M中各边的端点 匹配数 匹配数 B1=3 β=4 极大匹配 完美匹配 最大匹配 M饱和点 ●M-饱和点
匹配(边独立集):互不相邻的边的集合 M-饱和点:匹配M中各边的端点 匹配数 1=3 匹配数 1=4 极大匹配 最大匹配 完美匹配 M-饱和点 M-饱和点 图中的匹配

本节提要 口问题1:什么是二部图及其匹配? 口两个无内部边的顶点集;互不相邻的边的集合 口问题2:二部图中的有哪些匹配?
问题1:什么是二部图及其匹配? 两个无内部边的顶点集;互不相邻的边的集合 问题2:二部图中的有哪些匹配? 本节提要
二部图中的完备匹配 定义:设G是二部图,二部划分为,若G 中的匹配M饱和V,中所有顶点,则称M为V1到V2的 完备匹配。 注意:完备匹配一定是最大匹配,但仅当V1|=V2 才是完美匹配。 V到V2的完备匹配 存在完美匹配 无完备匹配?
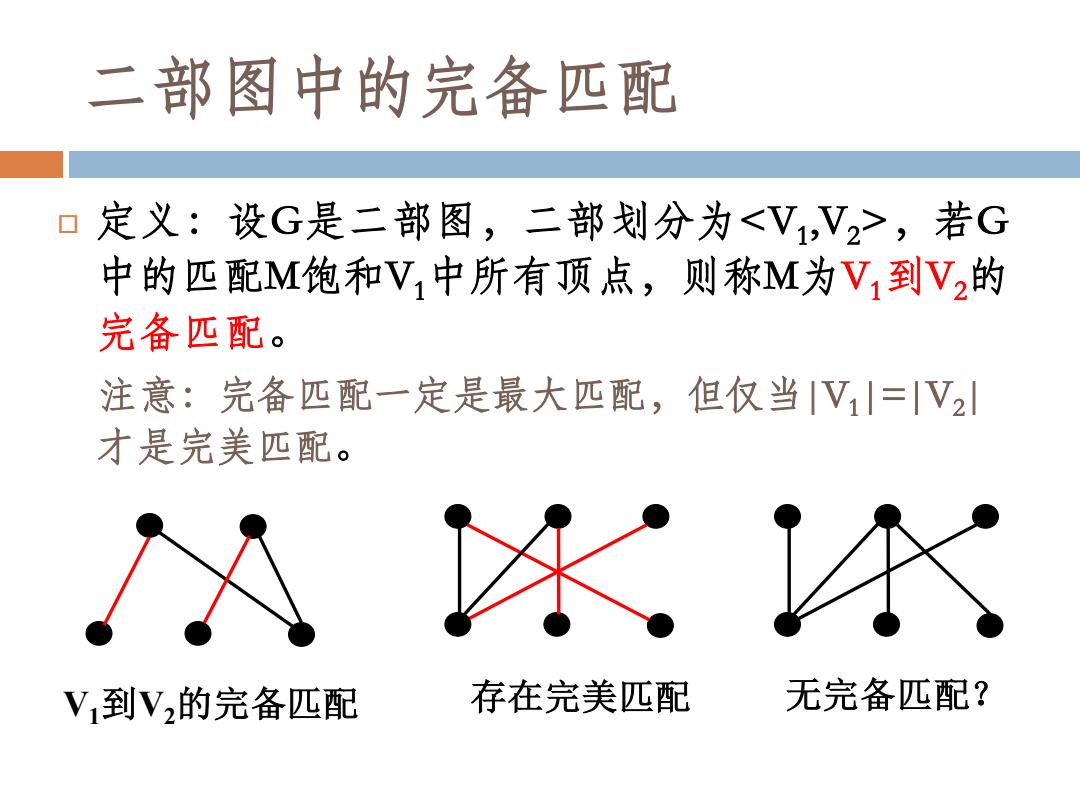
定义:设G是二部图,二部划分为,若G 中的匹配M饱和V1中所有顶点,则称M为V1到V2的 完备匹配。 注意:完备匹配一定是最大匹配,但仅当|V1|=|V2| 才是完美匹配。 V1到V2的完备匹配 存在完美匹配 无完备匹配? 二部图中的完备匹配
二部图中的完备匹配(举例) 口V1={1,2,3,4,5,6},是否存在饱和V1的配对方案? (A,C,F) B 2 3 {A,C} 饱和{1,3,4,6? 4 {A,F} 5 6 {C,F} G
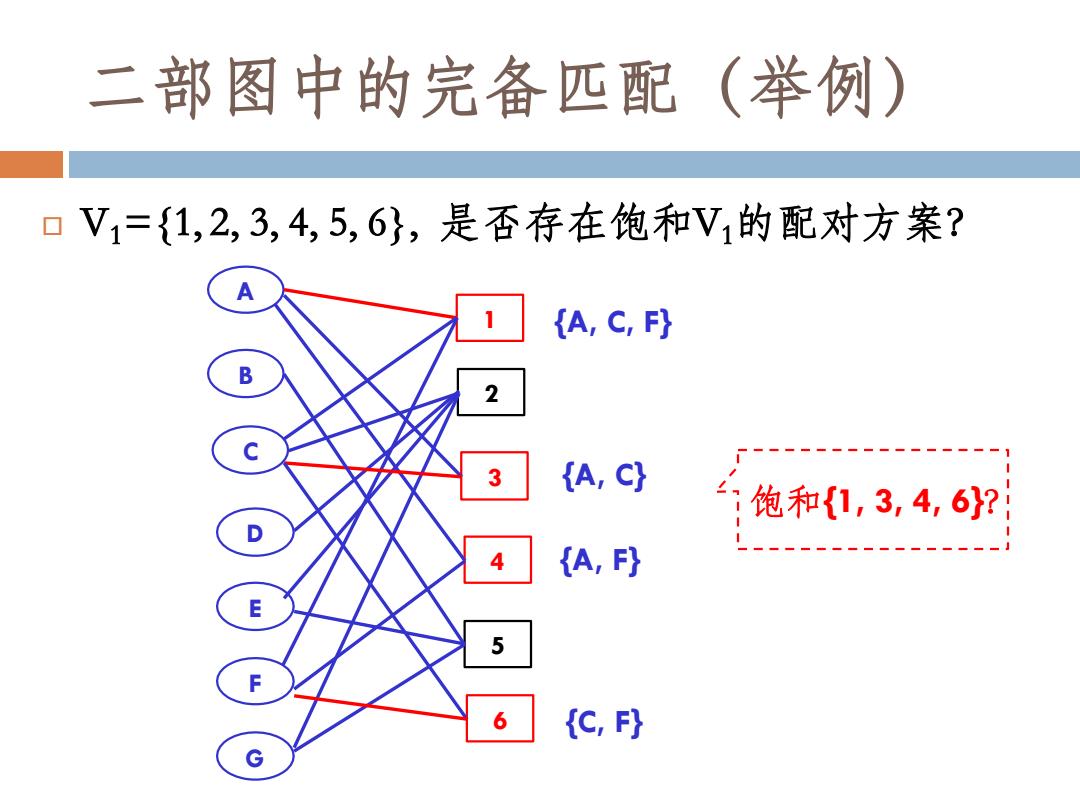
V1={1, 2, 3, 4, 5, 6}, 是否存在饱和V1的配对方案? A 1 B 2 C 3 D 4 E 5 F 6 G {A, C, F} {A, C} {A, F} {C, F} 饱和{1, 3, 4, 6}? 二部图中的完备匹配(举例)